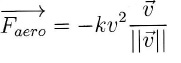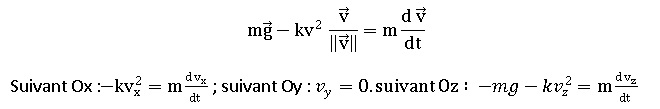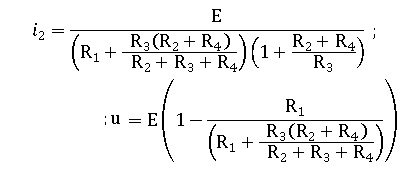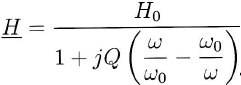Sciences
physique, Concours Emia 2019.
Ecole Militaire Interarmes.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
......
.....
|
Exercice 1- Étude du mouvement d'un projectile dans le champ de pesanteur uniforme. ( 6 points).
L'objet de I'exercice est l'étude du mouvement d'un projectile dans le champ de pesanteur terrestre.
Hypothèses.
- le référentiel terrestre est considéré comme galiléen,
- le champ de pesanteur est uniforme et caractérisé par le vecteur g,
- la résistance de l'air c'est à dire le freinage aérodynamique est négligê,
- le projectile de masse m est considêré comme ponctuel.
Description du problème.
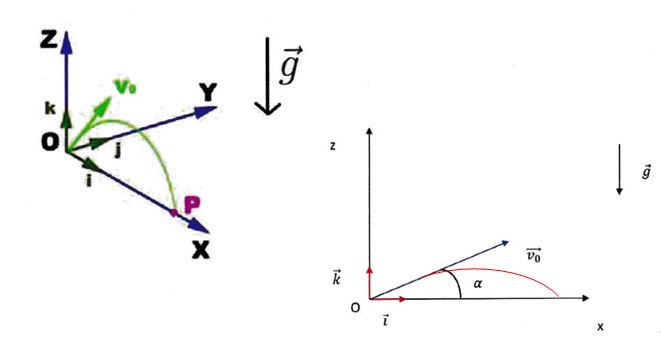
L'espace est rapporté au repère(artésien (O,x,y,z). La base associée est (O,i, j, k)
Le projectile est lancé, dans le plan vertical et à partir du point O, avec le vecteur vitesse initiale v0.Le vecteur vitesse fait un angle a, avec l'axe Ox.
La position du projectile, à chaque instant, est définie par la vecteur position OM.
Le projectile tombe au point P sur l'axe Ox.
Questions.
1. En utilisant le
principe fondamental de la dynamique, déterminer les équatiions du
mouvement du projectile,c'est à dire,les équations paramêtriques
x(t), y(t) et z(t) en fonction de v0, a, g, et t.
Le projectile n'est soumis qu'à son poids. Les vecteurs g et vitesse
initiales sont contenus dans le plan (xOz). Le mouvement s'effectue
dans ce plan ( y(t) = 0 ).
Coordonnées de l'accélération : 0 ; 0 ; -g.
Coordonnées de la vitesse initiale : v0 cos a ; 0 ; v0 sin a .
Coordonnées du vecteur vitesse : v0 cos a ; 0 ; -gt+ v0 sin a
Coordonnées du vecteur position ; x(t) = v0 cos a t ; y(t) =0 ; z(t) = -½gt2+ v0 sin a t.
2. En déduire l'équa!ion de la trajectoire, Ie nom de la forme de la trajectoire.
Représenter son allure sur un schéma.
t = x /(v0 cos a) ; repport dans z(t) : z(x) = -½g x2 /(v0 cos a)2 +x tan a.
Il s'agit d'une branche de parabole.
3. Déterminer I'expression de la distance OP, appelée portée, en fonction de v0, a, g.
z(t) = 0 ; -½g x2 /(v0 cos a)2 +x tan a = 0 ;
x = 0 ( position initiale) et x = 2 v02 sin a cos a / g = v02 sin ( 2a) / g.
4. Pour quel angle de niveau (a), la portée est-elle maximale ? La valeur de l'angle sera donnêe en degrés.
La portée est maximale pour sin ( 2a) = 1 soit a = 45°.
5. Donner l'expression de la portée maximale, notêe XM.
xM = v02 / g.
On applique les résultats précédents aux obus tirês par le canon de 155 mm monté sur le CAESAR.
Quelques données
- La valeur de I'intensité de la pesanteur est g =9,81 m s-2 - Les obus ont une masse moyenne de 43 kg.
- La portée maximale est 42 km.
On se place dans le cas des conditions de tir pour une portée maximale.
Pour faciliter les calculs, la position de la bouche du canon est au point O (on néglige la hauteur de la bouche).
6. A partir des données, en déduire la valeur de vitesse initiale v0. Le résultat sera donnê en m /s ainsi qu'en km/h; les valeurs seront arrondies à la valeur entière la plus proche.
v0 = (g xM)½ = (9,81 x 4,2 104)½ =641,887 ~642 m /s.
ou 641,87 x3,6 = 2310,8 ~2311 km / h.
7. Déterminer la
flèche c'est à dire la hauteur maximale atteinte par l'obus. Le
résultat sera donnê en km arrondi à la valeur entière la plus proche.
Au sommet de la parabole, la composante verticale de la vitesse est nulle.
-gt+ v0 sin a = 0 ; t = v0 sin a / g, repport dans z(t) :
zmaxi = -½g( v0 sin a / g )2+ v0 sin a ( v0 sin a / g ) = ½( v0 sin a )2/ g .
zmaxi =0,5 (641,887 x sin 45)2 / 9,81 ~10499 m ~ 10 km.
8. Calculer l'énergie cinétique de I'obus lorsqu'il arrive à son point d'impact P.
Le projectile n'est soumis qu'à son poids : son énergie mécanique se conserve.
Le point O et le point P sont sur l'axe Ox, horizontal, l'énergie potentielle de pesanteur est la même en O et en P.
L'énergie cinétique en P est égale à l'énergie cinétique en O.
½mv02 = 0,5 x43 x641,8872 ~8,9 106 J.
9. La cible ne se trouve pas à 42 km sur I'axe Ox mais à38 km, déterminer les valeurs des deux angles de niveau (a1 et a2) qui permettent d'atteindre cette cible.
xP= v02 sin ( 2a) / g. sin ( 2a) = xP g / v02 =38 103 *9,81/ 641,8872 = 0,905.
a1 = 32° et a2 =90-32=58 °.
Pour
les questions suivantes, on s'intéresse à la trajectoire pour laquelle
l'angle de tir est inférieur à l'angle correspondant à la portée
maximale déterminé à la question 4 (tir plongeant).
10. Déterminer le temps mis par l'obus pour atteindre le point d'impact.
xP =v02 sin ( 2a) / g= v0 cos a t ; t = 2 v0 sin a / g = 2 x641,887 / 9,81 sin a ~ 131 sin a.
11. Déterminer l'altitude z1 atteinte par l'obus 10 s après la sortie du canon.
z(t) = -½gt2+ v0 sin a t = -9,81 / 2 x102 + 10 v0 sin a~ -490,5 +6,42 103 sin a.
12. Déterminer l'énergie potentielle de l'obus à cet instant ainsi que son énergie cinétique.
L'énergie potentielle est considérée comme nulle lorsque z = 0.
Epp = m g z = 43 x9,81 (-490,5 +6,42 103 sin a)= 421,83 (-490,5 +6,42 103 sin a )= -2,07 105+2,71 106 sin a.
Ec = ½mv2 = 21,5 (( v0 cos a )2 +( -10g+ v0 sin a )2)=21,5 ( v02+(10g)2 -20g v0 sin a).
Ec = 21,5( 641,8872+98,12-20 x9,81 x641,877 sin a) =21,5(4,21 105-1,26 105 sin a)= 9,05 106 -2,71 106 sin a.
13. Déterminer I'ênergie mécanique à cet instant.
Epp + Ec = -2,07 105 +9,05 106 ~8,84 106 J ( 0,5 x43 x641,8872) ~8,84 106 J
14. Est-elle êgale à l'énergie cinétique de l'obus à Ia sortie du canon. Justifier la rêponse.
Oui, l'obus n'est soumis qu'à son poids, force conservative.
Dans cette partie, on ne néglige plus la résistance de l'air.
Le modèle de force de freinage aérodynamique est 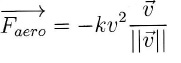
avec v vecteur vitesse du projectile.
15. Déterminer l'unité de k.
k est une force ( N ou kg m s-2) divisé par une vitesse au carré (m2 s-2).
k s'exprime en kg m-1.
16. Dêterminer les trois équations,différenllelles vérifiées par les trois composantes du vecteur vitesse.
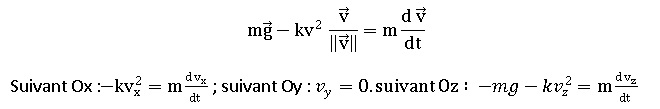
Remarque : ces équations ne peuvent pas être résolues analytiquement.
|
...
|
|
Exercice 2. Etude du radar de mesure balistique. ( 4 points )
Un radar, dénommé radar de mesure balistique, est installé sur le canon de 155 mm, monté
sur Ie CAESAR. Il permet de dêterminer la vitesse de l'obus à la sortie du canon.
Le principe physique de la mesure de la vitesse est basé sur l'effet Doppler.
Données
- la cêlérité de la lumière est c:3.108 m/s
- La frêquence d'êmission de l'onde émise par le radar esl fe - 10,525 GHz.
Questions.
1. Est ce qu'une onde électromagnétique est transversale ou longitudinale ?
Les champs magnétique et électrique étant perpendiculaires à la
direction de propagation, l'onde électromagnétique est transversale.
2. Quelles sont les grandeurs qui se propagent dans le cas d'une onde électromagnétique ?
Le champ magnétique et le champ électrique se propagent.
3. Calculer la période T. de l'onde émise par le radar.
T = 1 / fe = 1 / (10,525 106) = 9,5012 10-8 s.
4. Calculer la longueur d'onde de l'onde émise par le radar.
l = c / fe = 3,00 108 /(10,525 106) =28,5 m.
Principe de la mesure par effet Doppler.
Premier cas.
L'axe du canon constitue un axe x'x. Pour simplifier les calculs, on
considère que le radar est sur cet axe. Il est immobile. Sa position
est le point O de l'axe x'x. Ce point est pris comme origine des
abscisses. L'obus se déplace suivant cet axe Or.Il se déplace vers les
x >0 avec une vitesse v, considérée comme constante. Son mouvement
est supposé rectiligne sur la distance parcourue lors de la mesure.
La source (le radar) émet des ondes électromagnétiques de fréquence fe.
Ces ondes êlectromagnétiques atteignent le mobile et sont réfléchies
par celui-ci en direction du radar. Il est également récepteur.
On considère que le radar émet un signal continu en fonction du temps.
Pour le raisonnement, le début de Ia période du signal est associé à
l'émission du premier top qui se déplace à la célêrité c.
La fin de la première période (le début de la deuxième période) est
associé à l'émission d'un second top, qui se déplace à la célérité c.
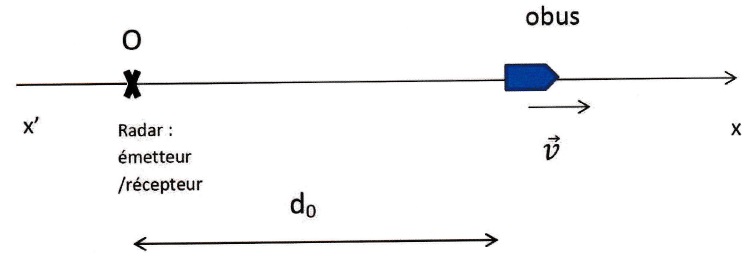
A Ia date t : 0 s, le radar émet un top et l'obus est à la distance d0 du point O.
5. Dêterminer l'équation horaire du top c'est à dire xondes(t),
à l'aller : xondes(t) = ct.
6. Déterminer l'équation horaire de l'obus c'est à dite xobus(t).
xobus(t) = vt + d0.
7. Déterminer l'instant t1 auquel le top atteint l'obus en fonction de d0, c et v.
ct1 = vt1+d0 ; t1 = d0 / (c-v).
8. En déduire la position de I'obus lorsqu'il est atteint par le signal en fonction de d0, c et v.
x1= vt1 + d0 =d0 ( v / (c-v) +1 ) = d0 c / (c-v).
9. A quel instant, tR1,le top réfléchi par l'obus est-il reçu par le radar ?
tR1 =2t1= 2 x1 / c = 2d0 / (c-v) .
A la date t = Te le radar émet un deuxième top.
10. Déterminer l'équation horaire de ce deuxième top c'est à dire xonde2(t).
à l'aller : xonde2(t) = c(t-Te).
11. Déterminer l'instant t2 auquel le top atteint l'obus en fonction de d0, c, v et Te.
xobus = xonde2 ; v t2 +d0 = c(t2-Te).
t2 = (d0 +cTe) / (c-v).
12. En déduire la position de l'obus x2 lorsqu'il est atteint par le signal en fonction de d0, c, v et Te,
x2 = vt2 + d0 = v (d0 +cTe) / (c-v) + d0 =c / (c-v) (d0 +vTe).
13. A quel instant le top réfléchi par I'obus tR2 est-il reçu par le radar ?
tR2 = x2 / c +t2 =(d0 +vTe) / (c-v) + (d0 +cTe) / (c-v) =(2d0 +(c+v) Te) / (c-v).
14. Déterminer I'écart temporel tR2-tR1.
tR2-tR1.=(2d0 +(c+v) Te) / (c-v) -2d0 / (c-v) =(c+v) Te / (c-v)
15. En déduire la fréquence du signal reçu par le radar fR.
fR =1 /(tR2-tR1) = (c-v) / (c+v) fe.
16. Montrer alors que la différence de fréquences entre la fréquence émise et la fréquence reçue a pour expression
fR-fe = -2v fe / (c+v).
fR-fe = (c-v) / (c+v) fe.-fe = -2v fe / (c+v).
La céléritê de propagation de l'onde électromagnétique, c, est très supérieure à la vitesse de l'obus en sortie du canon.
17. Montrer que la diffêrence de fréquences peu s'écrire fR-fe ~-2v fe / c.
c+ v ~ c ; fR-fe ~-2v fe / c.
Application numérique :
La différence de fréquences mesurée est 56, 133 kHz.
18. Calculer la vitesse de sortie de l'obus.
v = 56133 x 3,00 108 / (2x10,525 106) ~800 m / s.
|
....
|
Exercice 3. électrocinétique. 5 points
Première partie :
Soient deux rêsistances R1 et R2 en série.
1. Rappeler l'expression de la résistance équivalente Réq.
Réq = R1 +R2.
Soient deux résistances R1 et R2 en parallèle
2. Rappeler l'expression de la résistance équivalente.
1 / Req = 1 / R1 + 1 / R2 ; Req = R1R2 /(R1+R2).
On considère le montage suivant :
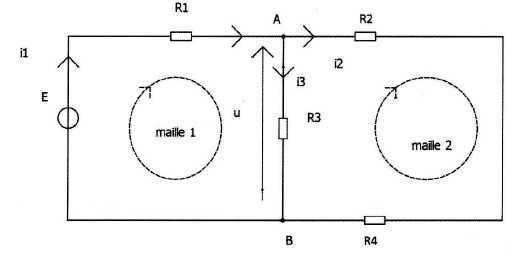
E = 5 V ; R1 = 100 ohms ; R2 = R4 = 25 ohms ; R3 = 50 ohms.
3. Quelle est la relation entre les intensités des courants i1, i2 et i3 ? Justifier la réponse.
Au noeud A : i1 = i2 + i3..
4. Écrire la loi des mailles dans les mailles 1 et 2.
E = u +R1i1 ; u =R3 i3 ; u = (R2 +R3) i2.
5. A partir des trois relations précédentes, déterminer l'expression littérale de l'intensité du courant i2.
R2 et R4 sont en série, R5 = R2 + R4 = 50 ohms.
R5 et R3 sont en dérivation : R6 = R5R3 / (R5 +R3) = 50 x 50 /(100) = 25 ohms.
R1 et R6 sont en série : Req = R1 + R6 = 125 ohms ; i1 = E / Réq = 5 / 125 = 0,04 A..
R5 i2 = R3 i3 ; i3 = R5 i2 / R3 = i2.
i2 +R5 i2 / R3 = E /Req ; i2 = E / (Req (1+R5 / R3)) = 5 / (125 ( 1+1))=0,02 A.
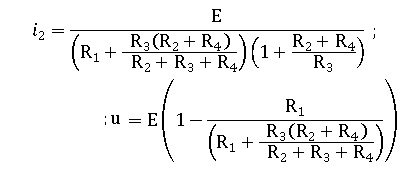
6. Déterminer l'expression littérale de la tension u aux bornes de la résistance R3.
u = R3i3 = E-R1i1 =E - R1 E / Réq = 5-5 x100 / 125 = 1 V.
7. Calculer les valeurs de la tension u et du courant i3.
i3 = u / R3 = 1 / 50 = 0,02 A.
8. Donner l'expression littérale de la puissance dissipêe par la résistance R3.
P = R3i32 = u2 / R3.
Seconde partie. Pont de Wien.
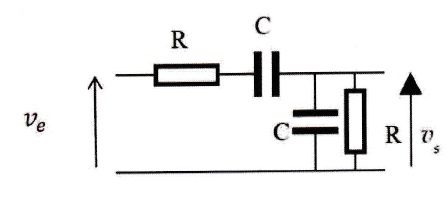
La tension d'entrée u, (ü) est une tension sinusoidale de la forme u(t)=V0cos(wt).
9. Rappeler l'expression de l'impédance complexe de la capacitê C .
1 / (jCw) = -j / (Cw).
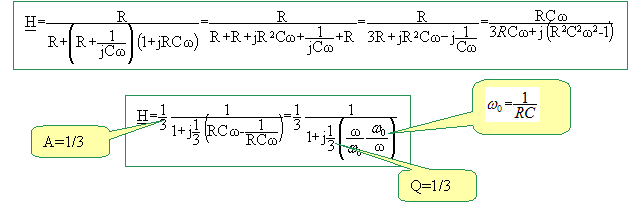
10. Déterminer I'expression littérale de la fonction de transfert H = vs / ve. la mettre sous la forme :
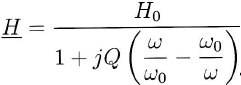
11. Donner les expressions de H0, Q et w0.
Admittance complexe des branches en dérivation :
Y= 1/R + jCw =
(1+RCw )/R
Impédance complexe correspondante :
Z1=R/(1+RCw)
Impédance complexe de l'ensemble : Z =
R+1/(jCw) + R/(1+RCw)
H= vs /ve =
Z1 / Z.
12. En déduire le gain G= |H|.

13. Déterminer I'expression de Ia pulsation w pour laquelle le gain est maximal.
14. Déterminer l'expression du gain pour cette pulsation.
Quand x=1, GdB =20 ln A= 20 ln(1/3) = -20 ln3
= -10.
15. Quet est le type de filtre de ce pont ?
C'est un filtre de bande centré sur w0.
Application numérique : Les valeurs de la résistance et de la capacité sont respectivement
R: 10 kW et C : 33 nF.
16. Calculer les valeurs de la pulsation w0 et de la frêquence de coupure f0.
w0 = 1 / (RC) = 1 / (104 x33 10-9) =3,03 103 ~ 3,0 103 rad/s.
f0 = w0 / (2p) = 3,03 103 / 6,28 ~4,8 102 Hz. |
|