Concours
Formation des ingénieurs de l'école nationale supérieure maritine 2019.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
......
.....
|
Exercice 1. Les vagues géantes de Nazaré. 8 points.
Partie I : Formation de la houle de haute mer
1.1. Au large de
Nazaré, un vent fréquent exerce une pression à la surface de l'eau. Peu
à peu, la mer encore calme passe alors d'un léger frémissement à une
houle qui se propage vers la côte.
1.1.a. Justifier que la houle est une onde mécanique progressive.
La houle est la propagation à la surface de l'eau d'une perturbation créée par le vent.
1.1.b. Choisir entre transversale ou longitudinale pour qualifier l'onde se propageant à la surface de l'eau. Justifier.
Onde transversale : l'onde se propage suivant l'horizontale et la mer se déforme suivant la verticale.
1.2. Une sonde à
vagues a été placée sur le passage de la houle afin d'enregistrer la
déformation de la surface de l'eau au cours du temps.
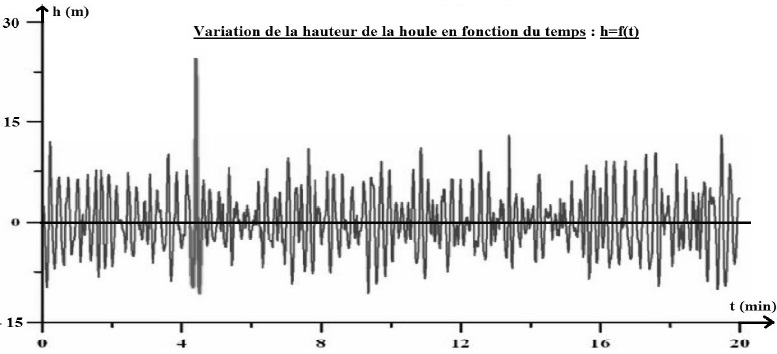
1.2.a. Dire s'il est vraiment exact de qualifier cette houle d'onde périodique. Justifier.
Il vaudrait mieux utiliser le terme pseudo-périodique, l'amplitude n'étant pas constante.
1.2.b. Evaluer la durée moyenne qui sépare le passage de deux vagues.
90 vagues se succèdent en 20 minutes : 20 / 90 = 0,222 min ~ 13 s.
1.2.c. Montrer que la fréquence des vagues est de l'ordre de f=0,075 Hz.
f = 1 / 13 ~ 0,075 Hz.
1.2.d. Vérifier l'exactitude de la hauteur de vague annoncée dans l'article ( une vingtaine de mètres).
L'amplitude du plus grand pic est voisine de 24 m.
1.3. Dans le document 2, il est mentionné la « longueur d'onde de la houle λ ».
1.3.a. Définir ce terme de façon générale, c'est à dire pour tout type d'onde.
La longueur d'onde est la distance parcourue par le front d'onde en un période T à la célérité v.
1.3.b. Expliquer ce qu'il représente concrètement dans le cas de la houle.
La longueur d'onde est la distance entre deux crêtes successives.
1.3.c. Montrer, d'après le document 2, qu'on peut écrire pour la houle de haute mer l = g / (2pf2).

En eau profonde l << h ; le nombre 1 est négligeable devant le terme en exponentielle.
c ~(gl / ( 2p))½ ; c 2~(gl / ( 2p) ; l ~ 2pc 2/ g avec c = l f ; l = g / (2pf2).
1.3.d. Faire l'application numérique dans le cas de la houle enregistrée sur le document 1.
l = 9,81 / (2 x3,14 x0,0752) =277,56 ~278 m.
1.3.e. Calculer la vitesse de cette houle.
c = 277,56 x0,075 ~20,8 m /s.
Partie II : Formation des vagues géantes.
2.1. Donner les
deux spécificités d'un canyon de type « gouf » permettant d'expliquer
le déferlement de vagues géantes sur le rivage.
Un canyon sous-marin s'étend sur une longueur de 277 km, sur une
profondeur qui peut atteindre plus de 5 000 mètres, pour se réduire à
50 mètres en arrivant devant Nazaré.
Dans ce type de canyon, la houle finit par se diviser en deux, une
partie va être ralentie par les hauts fonds tandis que l'autre partie
continuera sa course le long canyon.
Quand la houle « rapide » arrive sur une pente de remontée relativement
forte, elle subit alors un effet de marche qui lui permet de s'ajouter
à la partie de houle « ralentie ».
L'effet cumulé des deux houles provoque des hauteurs de vagues exceptionnelles.
2.2. Montrer d'après sa topologie que le canyon de Nazaré appartient bien à la catégorie des « goufs ».
C'est une entaille profonde dans le talus continental dont l'extrémité est très proche du littoral.
2.3. João Vitorino explique dans le document 3 que « la houle finit par se diviser en deux entre le canyon et les hauts fonds ».
2.3.a. Expliquer ce phénomène.
Le canyon canalise la houle du large ; cette houle se propage
rapidement du fait de la profondeur tandis qu'une autre partie est
ralentie du fait des hauts fonds. A l'approche du littoral, une pente
forte permet à la houle rapide de rejoindre la houle ralentie. Cet
effet cumulé provoque des vagues géantes.
2.3.b. Montrer d'après le document 5, que ce phénomène n'est pas observable à toute profondeur.
2.3.c. Conclure sur les parties du canyon de Nazaré où ce phénomène est observable. Justifier.
Sur la plupart des plages en pente douce, les vagues se cassent sur un fond qui absorbe l'onde.
Par contre des vagues canalisées par un canyon sou-marin rocheux, très profond, se termine brutalement au niveau du littoral.
2.4. João Vitorino
explique dans le document 3 que « L'effet cumulé des deux houles
provoque des hauteurs de vagues exceptionnelles ».
2.4.a. Nommer le phénomène physique auquel il fait implicitement référence. Justifier.
Superposition d'ondes mécaniques, interférences avec des ondes synchrones..
2.4.b. Schématiser une expérience avec la lumière permettant d'observer ce même phénomène.
 2.4.c. Expliquer les analogies entre votre expérience et la situation décrite à Nazaré.
2.4.c. Expliquer les analogies entre votre expérience et la situation décrite à Nazaré.
2.4.d. Expliquer par analogie la condition d'observation de « vagues exceptionnelles ».
Partie III : Le port de Nazaré.
3.1. João Vitorino évoque dans le document 3 le « déferlement brutal
des vagues, au pied du port de Nazaré, sur la Plage Nord (Praia do
Norte). ».
3.1.a. Estimer la vitesse des vagues à l'entrée du port de Nazaré, (profondeur ~ 50 m) en utilisant les documents 3 et 5.
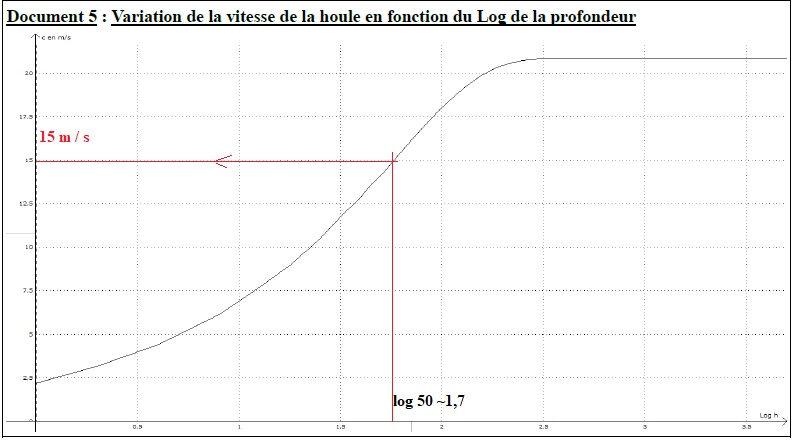
3.1.b. Evaluer alors l'espacement entre les vagues à cet endroit.
l = c / f =15 /0,075 =200 m.
3.2. Le document 6 montre l'implantation du port de Nazaré sur la côte.
3.2.a. Nommer le phénomène physique susceptible de se produire à l'entrée du port. Justifier.
La largeur de l'entrée du port ( environ 120 m) est du même ordre de
grandeur de la longueur d'onde des vagues. Un phénomène de diffraction
des ondes peut se produire.
3.2.b. Dire si il est observable lors de l'arrivée de la houle enregistrée dans le document 1. Justifier.
La largeur de
l'entrée du port ( ~ 120 m) est du même ordre de grandeur de la longueur d'onde
des vagues ( 278 m). Un phénomène de diffraction des ondes peut se produire
3.2.c. Expliquer le devenir de la houle après son entrée dans le port, à l'aide de calculs pertinents et d'un schéma à l'échelle .
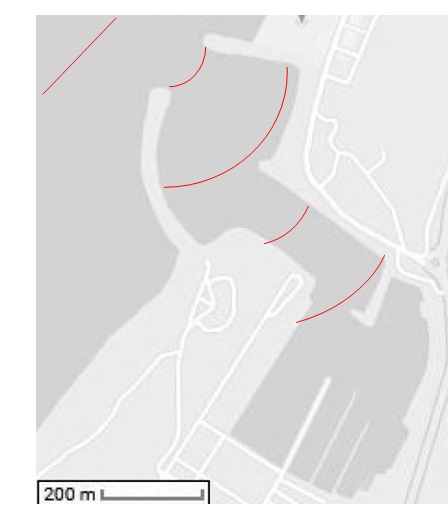
3.2.d. Conclure quant à l'architecture singulière de ce port.
Les bateaux ne peuvent pas être atteints par les vagues.
|
...
|
|
Surfer sur une vague géante. 7 points.
Surfeur : masse : mS = 75 kg
■ Planche :masse : mP = 5,9 kg ; longueur : L = 275 cm ; largeur : l = 67,5 cm ; épaisseur : e = 6,0 cm
■ Vagues : hauteur : h = 25 m ; période : T = 13 s ; fréquence : f = 0,075 Hz ; vitesse : c = 15 m.s-1 ; longueur d'onde : λ = 200 m
■ Divers : masse volumique de l'eau : μmer = 1,1 kg.L-1 ; accélération de la pesanteur : g = 9,8 m.s-2.
Partie I : Attendre la vague.
Rappel : tout corps immergé dans un fluide subit de la part de ce
fluide une poussée verticale dite « poussée d'Archimède », d'intensité
égale au poids du volume de fluide déplacé.
Le système {surfeur + planche} est immobile sur l'océan. Il attend la vague.
1.1. Faire un bilan complet des actions mécaniques qui s'exerce sur lui, schéma à l'appui.
Le système est soumis à son poids et à la poussée d'Archimède. Le système étant immobile, ces deux forces sont opposées.
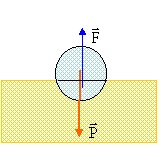
1.2. Calculer l'épaisseur e' de planche alors immergée sous l'eau.
Poids total : (75 +5,9) x9,8 =792,82 N.
Volume immergé : V = 2,75 x 0,675 e' = 1,856 e'.
Poussée : µmer V g =1,1 103 x1,856 e' x9,8 = 2,00 104 e'.
e' = 792,82 / (2,00 104) =3,96 10-2 m ~4,0 cm.
Partie II : Prendre la vague.
Dans cette partie du problème, tout frottement sera négligé.
2.1. Expliquer pourquoi un surfeur doit nager pour prendre une vague qu'il voit s'approcher au loin.
La vague étant au loin, le surfeur est immobile au bord du rivage et il ne peut pas attendre que la vague déferle.
Pour information, le record mondial sur « 200 m nage libre » est de 1 min 42 s.
2.2. Montrer qu'il est obligatoire que le système {surfeur + planche} se fasse tracter par un jet ski pour surfer cette vague.
Vitesse du nageur : 200 / (60 +42) =1,96 m /s, valeur très inférieure à la vitesse de la vague.
2.3. Calculer la valeur minimale de l'accélération aS
que doit avoir le système {surfeur + planche} pour surfer cette vague.
On supposera cette accélération constante au cours du déplacement. Le
surfeur est certainement lancé à plus de 80 km/heure (80 / 3,6)
~22,2 m /s.sur sa planche.
Le surfeur immobile doit acquérir une vitesse de 15 m / s en une durée inférieure ou égale à 13 s.
accélération = variation de la vitesse / durée = 15 / 13 ~1,16 ~1,2 m s-2.
2.4. En déduire la valeur de la force de traction FT que le jet ski doit exercer.
FT = (75 +5,9) x 1,16 ~ 93 N.
|
....
|
Partie III : Surfer la vague par un déplacement longitudinal.
Le système {surfeur + planche} se trouve désormais au sommet de la
vague géante. Il profite alors de la part de la vague d'une force de
poussée importante.
Dans cette partie du problème, on modélisera l'action mécanique de la
vague par un vecteur orienté comme la vitesse de propagation de l'onde,
d'intensité constante FP = 200 N.
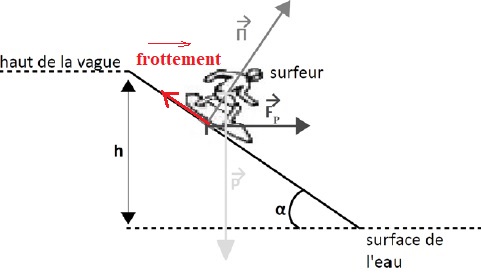
Le système {surfeur + planche} se déplace sur la surface de la vague,
assimilée à un plan incliné d'un angle α = 50°, par rapport à la
surface de l'eau au repos.
Il est soumis à 3 forces :
• son poids P
• la poussée de l'eau Π
• la poussée de la vague Fp.
3.1. Calculer l'énergie cinétique Ec0 du système {surfeur + planche} au sommet de la vague.
Ec0= 0,5 (75 +5,9) x152 =9,1 103 J.
3.2. Calculer le travail de chacune des trois forces lors du
déplacement rectiligne du système {surfeur + planche}, du haut de la
vague jusqu'à la surface de l'eau au repos.
Travail moteur du poids en descente : W=(mS +mP) h g=(75+5,9) x25 x9,8 =1,98 104 J.
Travail moteur de la poussée de la vague : W1 = FP h cos a = 200 x 25 xcos 50 = 3,21 103 J.
La poussée d'Archimède, perpendiculaire à la vitesse, ne travaille pas.
3.3. En déduire l'énergie cinétique EcF du système {surfeur + planche} au bas de la vague.
EcF - Ec0 = W +W1; EcF =9,1 103 +3,21 103 +1,98 104=3,21 104 J.
3.4. Montrer qu'avec ces hypothèses de travail, le surfeur sort de la vague avec une vitesse de l'ordre de 100 km.h-1.
v =(2EcF / (mS+mP))½ =(3,21 104 /80,9)½ =28,171 m s-1 ou 28,17 x3,6 ~100 km / h.
3.5. L'article de journal consacré à Benjamin Sanchis annonce une vitesse de sortie de vague autour de 80 km.h-1.
3.5.a. Nommer l'action mécanique qui a été oubliée ?
Les forces de frottement représentée ci-dessus ( même direction que la vitesse mais de sens contraire)
3.5.b. Reprendre sur votre copie le schéma proposé en modélisant cette
action mécanique par une force unique, s'opposant au mouvement du
système.
3.5.c. Calculer le travail de cette force au cours du déplacement.
Reprendre à cet effet le raisonnement de la question 3.2. Interpréter
le résultat.
Energie cinétique réelle à la sortie de la vague ( v =80 /3,6 ~ 22,2 m /s) :
0,5 x80,9 x22,22 ~ 2,0 104 J.
Travail résistant = diminution de l'énergie cinétique = (2,0 -3,21) 104 = -1,2 104 J.
3.5.d. En déduire la valeur de cette force. On supposera qu'elle reste constante au cours du déplacement.
-1,2 104 = - f h / sin a ; f = 1,2 104 sin 50 / 25 =3,7 102 N.
3.5.e. Discuter de la vraisemblance de cette hypothèse.
Cette valeur est réaliste. La force de frottement n'est sans doute pas constante.
|
Exercice III : L'éliodomestico, un désalinisateur solaire (5 pts).
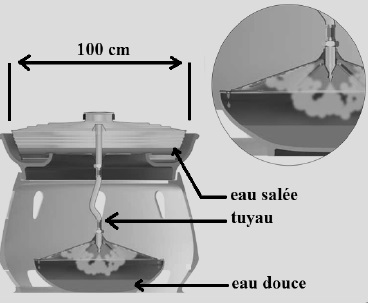
L’eau de mer est placée dans la partie haute, surmontée d'un couvercle noir étanche.
Exposé en plein soleil, l’eau est chauffée et s’évapore naturellement tandis que le sel reste.
La vapeur d’eau est alors collectée par un tuyau et envoyée dans le
conteneur du dessous où refroidie, elle se condense en eau douce,
dépourvue de sel.
D'après www.eau-nature.fr
• Chaleur latente de vaporisation de l'eau à 60°C : LV = 2,31 MJ.kg-1
• Capacité thermique massique de l'eau liquide : ceau = 4,18 kJ.kg-1.°C-1
• Masse volumique de l'eau : μeau = 1,00 kg.L-1
• Puissance surfacique solaire moyenne sur un jour complet : PS = 280 W.m-2.j-1.
Rappels
• La chaleur latente de vaporisation de l'eau est l'énergie mise en jeu
lors de la transformation d'un kilogramme d'eau liquide en vapeur.
• La surface S d'un disque de rayon R est : S=πR2.
On s'intéressera dans ce problème à la partie haute de l'éliodomestico.
1.a. Nommer les types de transferts thermiques qui permettent de
chauffer l'eau dans la partie haute de l'éliodomestico. Justifier.
L'eau est exposée en plein soleil : rayonnement solaire.
Mouvement de convection dans le liquide et la vapeur.
Conduction à travers les parois..
1.b. Nommer le type de transfert thermique que le couvercle permet de limiter. Justifier.
Le couvercle noir limite considérablement la réflexion des rayons solaires.
1.c. Nommer celui qu'il ne peut empêcher. Justifier.
Transfert par conduction du corps chaud à travers les parois vers l'extérieur.
1.d. Identifier la principale de source de perte thermique. Expliquer.
Transfert par conduction du corps chaud à travers les parois vers l'extérieur.
2.a. Calculer la puissance solaire moyenne reçue par le couvercle de
l'éliodomestico sur une journée. On considèrera le couvercle de forme
circulaire.
Surface du couvercle S = 3,14 x0,502 =0,785 m2.
Puissance reçue : 0,785 x280 =2,2 102 W j-1.
2.b. Calculer la résistance thermique de l'éliodomestico nécessaire
pour maintenir constante une température interne à 60 °C. La
température externe des parois latérales est de 30 °C. On négligera
toute perte autre que par conduction.
R = puissance reçue / différence de température = 2,2 102 / 30 =7,33 ~7,3 K W-1.
2.c. Calculer de même la résistance thermique du couvercle de
l'éliodomestico sachant que dans ces conditions, la température de sa
surface extérieure est de 70 °C.
2,2 102 / 40 =7,33 ~5,5 K W-1.
3. On suppose que le récipient à une capacité thermique négligeable
devant celle de l'eau. L'eau de mer introduite dans l'éliodomestico a
initialement une température de Ti = 20,0 °C. La température interne de
l'appareil reste constamment égale à Tf = 60,0 °C.
3.a. Représenter sur un diagramme énergétique les échanges d'énergie
dont le système {eau + éliodomestico} est le siège. Discuter de leurs
signes.
Le système reçoit de l'énergie rayonnante du soleil ( comptée
positivement) et cède de l'énergie au milieu extérieur par conduction (
comptée négativement).
3.b. Calculer la variation d'énergie interne ΔUeau nécessaire pour adoucir les 5 litres d'eau quotidiens.
ΔUeau = meau ceau Dq + meau Lv =5 x4,18 x40 +5 x2,31 103 =836 + 1,155 104 =1,24 104 ~1,2 104 kJ = 12 MJ.
3.c. Montrer que les pertes thermiques sur une journée sont autour de 7 MJ.
Energie reçue : 2,2 102 x24 x3600 =1,9 107 J = 19 MJ ; pertes = 19-12=7 MJ.
3.d. Définir et calculer le rendement énergétique de l'éliodomestico.
Energie utile / énergie reçue = 12 / 19 ~0,63 ( 63 %).
|
|
|







