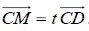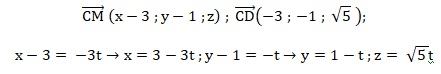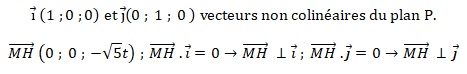Concours
Formation des ingénieurs de l'école nationale supérieure maritine 2019.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
......
.....
|
1ère question.
1. Soient f et g les fonctions définies sur respectivement par :
f (x) = x2e-x et g(x) = e-x .
Dans un repère orthonormé du plan, on note Cf et Cg leurs courbes représentatives.
1.1. Déterminer, par le calcul, les valeurs exactes des coordonnées des points d’intersection des deux courbes.
x2e-x =e-x ; x2 =1 ; x = ±1.
g(1) = 1 /e et g(-1) = e.
1.2. Etudier les positions relatives des courbes sur R.
f(x) -g(x) = e-x(x2-1) avec e-x positif.
Si x appartient à ]-1 ; 1[, f(x) -g(x) < 0, Cg au dessus de Cf.
Si appartient à ]-oo ; -1[ et à ]1 ; +oo[, Cg au dessous de Cf.
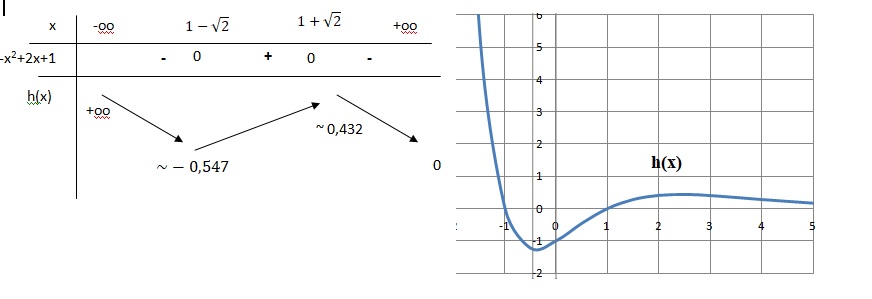
2. Soit h la fonction définie sur par h(x) = e-x(x2-1) .
2.1. On admet que lla limite en plus l'infini de ex / x2 est plus l'infini.
Déterminer les limites de la fonction h en +oo et en -oo .
h(x) = (x2-1) / ex =x2 / ex -1 /ex.
Quand x tend vers plus l'infini : x2 / ex et 1 /ex tendent vers zéro.
Quand x tend vers moins l'infini : e-x et x2 tendent vers plus l'infini.
2.2. Montrer que h'(x) est du signe de -x2 +2x+1.
On pose u = e-x et v = x2-1 ; u' = -e-x ; v' = 2x.
u'v +v'u =e-x( 1-x2+2x).
e-x étant positif, le signe de h'(x) est celui de -x2 +2x+1.
2.3. En déduire les variations de la fonction h sur , et dresser son tableau de variations.
Etude de -x2 +2x+1=0 ; discriminant D =22-4*(-1)=8.
Solutions : (-2 ± 2*2½) / (-2) = 1 ± 2½.
3. Soient les points A(x ; f (x)) et B(x; g(x)) pour x appartenant à [-1 ; +oo[.
On s’intéresse à la distance AB .
3.1. Montrer que :
AB = h(x) si x appartient à [1 ; +oo[ et AB = -h(x) si x appartient à [-1 ; 1].
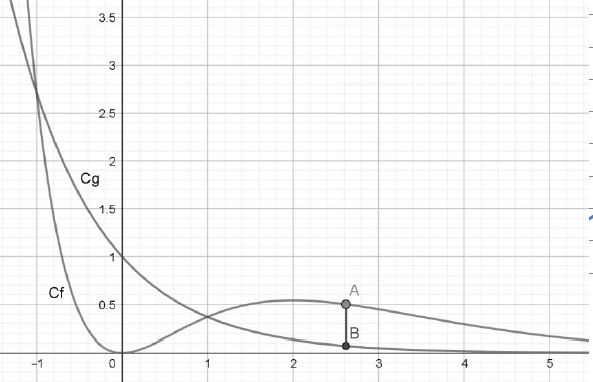
AB = |g(x) - f(x) |.
AB étant positif : AB = h(x) si x appartient à [1 ; +oo[ et AB = -h(x) si x appartient à [-1 ; 1].
3.2. Pour quelle valeur de x la distance AB est-elle maximale ? On notera x0 cette valeur.
Calculer la valeur exacte puis une valeur approchée à 10-3 près de la distance AB en x0 .
AB est maximale pour x0 = 1-2½ ~ -0,414.
AB = [(1-2½)2-1] exp(2½-1) =| 2 -2*2½| exp(2½-1) ~ 0,8284*1,513 ~1,254.
4. On s’intéresse, à présent, à l’aire A du domaine délimité par l’axe des abscisses, la courbe Cf et les droites
x = 0 et x =1. (La fonction f a été définie dans la question 1).
Afin d’obtenir une valeur approchée de S , on utilise la méthode dite «
des rectangles » qui consiste à approcher cette aire par la
somme des aires de n rectangles. Le graphique ci-dessous illustre cette méthode pour n =10 (le premier rectangle est d’aire
nulle car f (0) = 0 ). Le nombre n de rectangles choisi permettra,
lorsqu’on l’augmente, d’améliorer l’approximation de l’aire S.
4.1. Recopier et
compléter l’algorithme ci-dessus pour qu’en fin d’exécution, la
variable S contienne la valeur approchée par défaut de l’aire A obtenue
en utilisant la méthode « des rectangles » avec n rectangles.
Largeur d'un rectangle 1 / n ; hauteur du second rectangle : f(k / n).
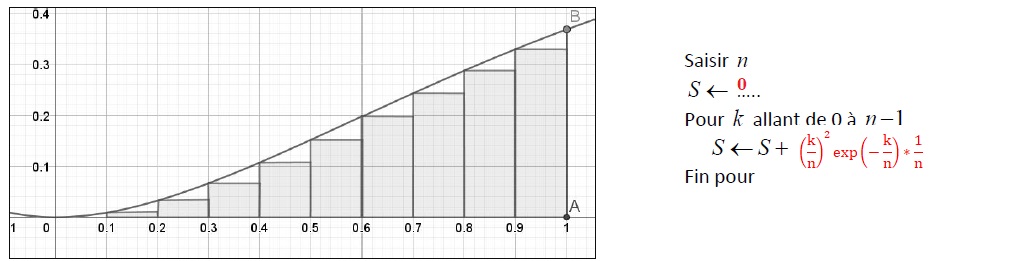
Pour n = 10, S = 0,1425 ; n=100, S = 0,1587 ; n = 100 000, S = 0,160.
4.2. Montrer que la fonction F définie sur par F(x) = (-x2- 2x - 2)e-x est une primitive de la fonction f .
On pose u = e-x et v = -x2-2x-2 ; u' = -e-x ; v' = -2x-2.
u'v +v'u =e-x( x2+2x+2-2x-2)= x2e-x = f(x).
4.3.
Déterminer à présent la valeur exacte de l’aire A . Votre résultat
est-il cohérent avec les valeurs de S obtenues précédemment ?
S = F(1)-F(0) = -5 / e +2 ~0,160. Résultats cohérents.
|
...
|
|
Question 2.
Un biologiste étudie le développement d’un certain type de parasite. Il place en milieu clos une colonie de 50 000 individus.
Des expériences ont démontré que dans ces conditions, à long terme, la
population se stabilise autour de 90 000 individus, sans jamais
dépasser cette valeur.
On considèrera que la population est « stable » lorsque le taux
d’évolution du nombre d’individus en une journée est inférieur à 0,1%.
1. Premier modèle.
Au bout d’une journée, il observe que la population s’élève à 54 000 individus.
Il décide de faire l’hypothèse suivante :
En notant pn le nombre d’individus, en milliers, au bout de n journées, la suite (pn) vérifie p0= 50 et pour tout entier naturel n , pn+1=0,9 pn+9.
1.1. Vérifier que ce modèle est en accord avec l’observation du nombre d’individus au bout d’une journée.
p1 = 0,9 p0+9 =0,9 x50 +0,9 =54 milliers.
1.2. On note vn = pn -90 .
Montrer que la suite (vn) est géométrique.
vn+1= pn+1-90 =pn+1= 0,9 pn+9-90 =0,9 ( pn-90)=0,9 vn.
1.3. En déduire l’expression de vn puis de pn en fonction de n.
vn = v0 x 0,9n ; pn = v0 x 0,9n +90 avec v0 = - 40
1.4. Ce modèle est-il compatible avec l’observation attendue à long terme ? Justifier.
Quand n tend vers plus l'infini, 0,9n tend vers zéro et pn tend vers 90 milliers.
1.5. Déterminer au bout de combien de jours cette population est considérée comme « stable ».
(90-pn) / 90 < 0,001 ; pn / 90 > 1-0,001 ; pn > 89,91.
v0 x 0,9n +90 >89,91 ; v0 x 0,9n >89,91 -90 ; 0,9n > -0,09 / (-40) ;
0,9n >0,00225
ln(0,00225) > n ln(0,9) ; n > 58.
2. Deuxième modèle.
Au bout de deux journées, il observe que la population d’élève à 57 888 individus.
Il décide d’adopter un nouveau modèle : En notant rn le nombre d’individus au bout de n journée, la suite (rn)
vérifie pour tout entier naturel n , rn+1=f(rn) où f est la fonction définie sur R par
f (x) = -0,002x2 +1,18x.
2.1. Justifier que ce modèle est en accord avec les décomptes de la population effectués les deux premiers jours.
r0 =50 ; r1 =f(r0) = -0,002 *50 2 +1,18*50 =54 milliers.
r2 =f(r1) = -0,002 *54 2 +1,18*54 =57,888 milliers.
2.2. Démontrer que pour tout entier naturel n , 0 < rn+1 < 90.
f '(x) = -0,004 x+1,18 ; f '(x) =0 pour x = 1,18 / 0,004 =295.
f '(x) est positive sur [0 ; 295[ ; f(x) est strictement croissante sur cet intervalle.
Initialisation : la propriété est vraie au rang zéro.
Hérédité : la propriété est supposée vraie au rang p.
0 < rp < 90 ; la fonction f étant strictement croissante et positive sur [0 ; 295[ :
f(0) < f(rp) < f(90) ; 0 < rp+1 < f(90) avec f(90) =90.
La propriété est vraie au rang p+1.
Conclusion : la propriété est vraie au rang zéro et héréditaire, elle est vraie pour tout n de [0 ; 295[ .
2.3. En déduire que la suite (rn) est convergente. On note l sa limite.
La suite (rn) est croissante et bornée, donc elle converge.
2.4. On admet que l doit vérifier f (l) = l . En déduire la valeur de l .
l = -0,002l2 +1,18 l ; -0,002l2 +0,18 l =0.
Solution retenue : l =0,18 /0,002 =90.
2.5.
Recopier et compléter l’algorithme ci-dessous pour qu’il affiche en
sortie le nombre de jour au bout duquel la population pourra être
considérée
comme stable.

|
....
|
Exercice 3.
Dans
une grande entreprise, un virus informatique a infecté 20% des
ordinateurs. Un technicien de la maintenance informatique doit les
contrôler à l’aide d’un logiciel anti-virus. Lorsqu’un ordinateur est
infecté par le virus, le logiciel émet un message d’alerte dans 95% des
cas. 27% des tests ont donné lieu à un message d’alerte.
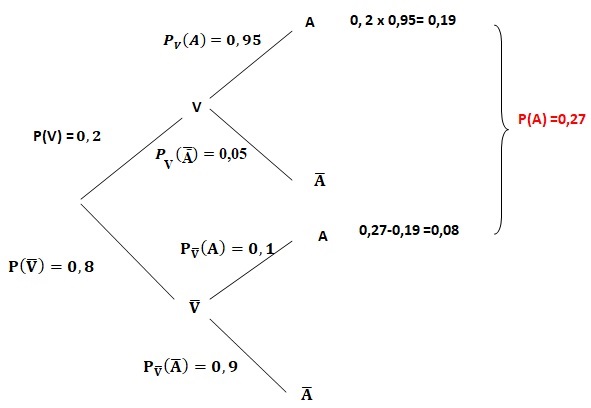
1. On choisit au hasard un des ordinateurs de l’entreprise, et on note les événements suivants :
V : « l’ordinateur est infecté par le virus »
A : « Le logiciel émet un message d’alerte »
1.1. Représenter cette situation à l’aide d’un arbre pondéré et calculer P(V n A).
1.2. Calculer P( nonV n A) et en déduire Pnon V (A) .
1.3. Le technicien reçoit un message d’alerte du logiciel anti-virus sur un ordinateur.
Il affirme qu’il y a alors moins de 3 chances sur 4 que cet ordinateur
soit effectivement infecté par le virus Justifier cette affirmation.
0,19 / 0,27 ~0,70 chance que l'ordinateur soit infecté.
0,08 / 0,27 ~0,30 chance qu'il ne soit pas infecté.
2. A chaque fois
qu’un message d’alerte est émis par le logiciel antivirus, le
technicien réalise un second test, parfaitement fiable celui-ci, pour
savoir si l’ordinateur est effectivement infecté par le virus. Le coût
de ce second test pour l’entreprise s’élève à 10 €. Si l’ordinateur est
effectivement infecté, il engage alors une réparation de la carte mère
dont le coût pour l’entreprise s’élève à 25 €.
Lorsque le logiciel antivirus n’a pas émis de message d’alerte,
l’ordinateur est remis en circulation, et le coût pour l’entreprise est
de 0 €.
On note X la variable aléatoire qui donne le coût total de l’intervention sur un ordinateur choisi au hasard dans l’entreprise.
2.1. Donner la loi de probabilité de X sous forme d’un tableau.
2.2. Calculer E(X) et interpréter le résultat obtenu.
On note N le nombre d'ordinateurs de l'entreprise.
|
Message d'alerte reçu
|
Pas de message d'alerte
|
| ordinateur infecté |
0,19 x (10 +25)N =6,65 N
|
0,01 x0
|
ordinateur non infecté
|
0,08 N x10= 0,8 N
|
0,72 x0
|
Total
|
7,45 N
|
0
|
2.3.
Le responsable du budget de la maintenance informatique demande au
technicien de ne pas pratiquer ce second test, et d’effectuer la
réparation de la carte mère sur tous les ordinateurs sur lesquels le
message d’alerte a été émis par le logiciel anti-virus. Justifier cette
décision.
0,27 x 25 N = 6,75 N, valeur inférieure à 7,45 N.
3.
Il choisit 400 ordinateurs pour les tester. Le parc informatique de
l’entreprise est suffisamment grand pour que ce choix puisse être
assimilé à 400 tirages successifs avec remise. On note Y la variable
aléatoire qui donne le nombre d’ordinateurs infectés parmi ces 400
ordinateurs.
3.1. Déterminer la loi de probabilité de Y en précisant ses paramètres puis calculer son espérance µ et son écart-type s .
Loi binomiale : les tirages sont indépendants ; chaque tirage conduit à deux issues possibles :
ordinateur infecté p =0,2, ordinateur sain q = 1-p = 0,8.
Espérance µ = np = 400 x0,2 =80 ; variance : npq = 400 x0,2 x0,8 =64 ; écart type : 64½ = 8.
3.2. Quel calcul donne la probabilité qu’au moins un ordinateur soir infecté par ce virus ?
Que peut-on dire de cet événement ?
P(Y > 1) = 1 -P(Y=0) = 1-1,7 10-39 ~ 1.
Cet événement est quasiment certain.
3.3.
Pour cette question, on utilisera l’approximation permise par le
théorème de Moivre-Laplace, c'est-à-dire que pour tous réels a et b ,
P( a < (Y-80) / 8 < b ~ P(a < Z < b) où Z suit la loi normale centrée réduite.
On utilisera la table de valeurs suivante pour répondre :

3.3.1. Calculer P(Y < 90).
P(Y < 90)= 0,894.
3.3.2. Déterminer un entier c tel que P( 80-c < Y < 80+c) ~ 0,9.
P(80-c < Y < 80+c) = 0,9 ; P(-c < Y-80 < c) = 0,9 ;
P(-c/ 8 < (Z < c / 8) = 0,9 ;
2P(Z < c / 8)-1 = 0,9 ; P(Z < c / 8) =0,95 ;
La table donne : c / 8 = 1,65 ; c ~13.
|
Exercice 4.
On se place dans un repère orthonormé de l’espace.
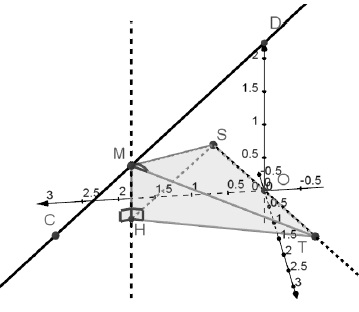

1.1. Déterminer une représentation paramétrique de la droite D , parallèle à la droite (AB) , passant par O, l’origine du repère.
Coordonnées d'un vecteur directeur de la droite (AB) :
(xB-xA ; yB-yA ; zB-zA) soit ( 1 ; -3 ; 0).
Représentation paramétrique de la droite D :
x = t +xO ; y = -3t +yO ; z = zO soit x = t ; y = -3t ; z = 0.
1.2. Montrer qu’il existe exactement deux points, appartenant à la droite D, situés à la distance 10½ / 2 du point O. Vous préciserez les coordonnées de ces deux points.
M (x, y, z) appartient à la droite D : MO2 =x2 +y2 +z2 =t2 +(-3t)2 = 10t2 = 10 / 4 = 2,5 ; t = ±0,5.
Coordonnées du premier point ( t = 0,5) : ( 0,5 ; -1,5 ; 0 ).
Coordonnées du second point ( t = -0,5) : ( -0,5 ; 1,5 ; 0 ).
1.3. Déterminer une équation cartésienne du plan Q , orthogonal à la droite (CD) , et passant par le point O.
Coordonnées d'un vecteur directeur de la droite (CD) :
(xD-xC ; yD-yC ; zD-zC) soit ( -3 ; -1 ; 5½).
Equation cartésienne du plan Q : -3x -y +5½z +d = 0.
L'origine O appartient à ce plan donc d = 0.
1.4. Montrer que la droite D est incluse dans le plan Q .
-3t -(-3t) +5½ *0 =0 est bien vérifié quelque soit t.
2. Soit t un nombre réel appartenant à [0;1] et M le point du segment [CD] vérifiant l’égalité vectorielle : 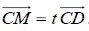
2.1. Déterminer les coordonnées de M en fonction de t.
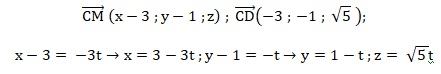
2.2. Montrer que le
point H (3-3t ; 1-t ; 0) est le projeté orthogonal de M sur le plan P
(C’est à-dire que H appartient à P et (MH) perpendiculaire à P ).
Le point P est le plan horizontal ( z = 0). Le point H appartient bien à ce plan ( zH=0).
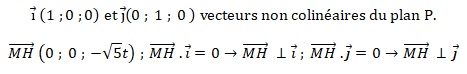
2.3. Montrer que le triangle TSH est isocèle en H puis déterminer une expression de l’aire du triangle TSH en fonction de t .
HS2 =(0,5-3+3t)2 +(-1,5-1+t)2 =6,25 +9t2-15t +6,25 +t2-5t=10t2-20t+12,5.
HT2 =(-0,5-3+3t)2 +(1,5-1+t)2 =12,25 +9t2-21t +0,25 +t2+t=10t2-20t+12,5.
S et T sont symétriques par rapport à O ; HO est une hauteur du triangle TSH.
HO2 =(3-3t)2 +(1-t)2 = 9+9t2-18t +1+t2-2t =10t2-20t +10 =10(t2-2t+1) =10(t-1)2 ; HO = 10½(1-t).
ST2 = (-1)2 +32 = 10 ; ST = 10½.
Aire du triangle TSH : ST x HO / 2 = 5(1-t).
2.4. En déduire que le volume V(t) de la pyramide TSMH peut s’écrire : V(t) =5 / 3 *5½ t(1-t).
V(t) = aire de base fois hauteur / 3 = aire du triangle TSH fois MH / 3.
V(t) = 5 (1-t) 5½t / 3.
2.5. Déterminer les coordonnées du point M0 permettant d’obtenir la pyramide de volume maximal.
On dérive V(t) et on cherche quelle valeur de t annule cette dérivée.
On pose u = t ; v = 1-t ; u' = 1 ; v' = -1 ; u'v+v'u = 1-t -t =0 soit t = 0,5.
M0( 1,5 ; 0,5 ; 5½ / 2).
2.6. Calculer la valeur du produit scalaire suivant :
2.7. En déduire la valeur de cos (SM0T) puis donner une valeur en degré, approchée à 0,1 près, de l’angle géométrique SM0T.
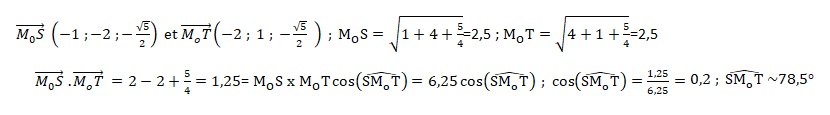
|
|
|