Mathématiques, Concours ESA 2018 ( école de santé des armées)

Mathématiques, Concours ESA 2018 ( école de santé des armées).

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

.
.

......

.....

Pour chacune des questions, une seule réponse est exacte. Toute réponse juste est comptée +1 point ; toute réponse fausse est comptée -0,25 point. Une absence de réponse est comptée 0 point.
QCM 1.
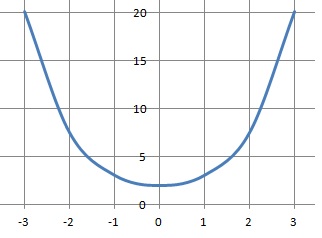
La fonction f définie sur R par f(x) = e^x+e^-x est :
A. Croissante sur ] -oo ; 0[ et décroissante sur [0 ; +oo[.
On dérive f ' (x) = e^x-e^-x= e^x( 1-e^-2x).
La dérivée est du signe de 1- e^-2x ; 1- e^-2x > 0 si e^-2x < 1 soit x > 0.

B. Croissante sur R.
C. décroissante sur ]-oo ; 0[ et croissante sur [0 ; +oo[. Vrai.
D. décroissante sur ]-oo ; -2[ et croissante sur [-2 ; +oo[

QCM 2.
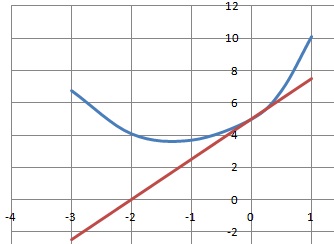
Soit f la fonction f définie sur R par f(x) = 5exp(0,2x² +0,5x).
La tangente à la courbe représentative de la fonction f au point d'abscisse zéro :
A. a pour équation y = 2,5x +5. Vrai.
On dérive f ' (x) =5(0,4x+0,5)exp(0,2x² +0,5x).
Coefficient de cette tangente a = f '(0) = 2,5.
La tangente passe au point de coordonnées ( 0 ; 5).
Equation de la tangente y = 2,5 x +5.

B. a pour équation y = 5x+10.
C. a pour équation y = 5x.
D. est parallèle à l'axe des abscisses.

QCM 3.
Les solutions de l'inéquation ln(-x+5) < ln(x+1) sont :
A. ] 2 ; +oo[.
-x+5 et x+1doivent être positifs : x < 5 et x > -1.
ln(-x+5) - ln(x+1) < 0 ; ln[(-x+5) /(x+1)] < ln(1).
(-x+5) / (x+1) < 1 ; -x+5 < x+1 ; 2 x >4 ; x > 2.
B. ]-oo ; 5[.
C. ]-1 ; 5 [
D. ]2 ; 5[. Vrai.

QCM 4
La limite en plus l'infini de (x²+1)^½-(x²-1)^½ est égale à :
A. +oo.
x(1+1/x²)^½- x(1-1/x²)^½ =x[(1+1/x²)^½-(1-1/x²)^½].
1/x² tend vers zéro quand x tend vers plus l'infini.
B. 1
C. 0. Vrai.
D. 2

QCM 5.
On choisit un réel au hasard entre 0 et 5 et l’on note Y la variable aléatoire égale au réel choisi. Alors :
A. P(Y = 2,5)=0,5
Une variable aléatoire qui peut prendre n valeurs possibles suit la loi uniforme. La probabilité de n'importe quelle valeur est 1 / n.
P(2 < Y < 3) = (3-2) / (5-0) = 1 /5.
B. P(Y < 2) = 0,5
C. P_{Y > 2} (Y < 3)= 1 /3.
D. P_{Y > 2} (Y < 3)= 1 /5. Vrai.

QCM 6.
Pour tout nombre réel x non nul, 2-(e^-x-2) / (e^-x-1) est égal à :
A. (3e^-x-4) / (e^-x-1)
Réduire au même dénominateur : (2e^-x-2-e^-x+2) / (e^-x-1)=e^-x /(e^-x-1) = 1 /(1-e^x).
B. 1 / (1-e^x). Vrai.
C. (e^-x-4) / (e^-x-1)
D. (3e^-x) / (e^-x-1).

...

Exercice 2.
QCM 7.
Dans un laboratoire, il y a 50 tubes avec du sang contaminé et 75 tubes avec du sang non contaminé. Un préparateur tire un tube au hasard, regarde si le sang contenu est contaminé et il replace le tube. Il recommence 5 fois l’expérience. On note X le nombre de tubes avec du sang contaminé (sur les 5 tirés).
A. P(X=5) =(3/5)⁵.
Probabilité de tirer un tube contaminé = 50 /(50 +75) = 2 / 5. P(X=5) =(2/5)⁵.
B. E(X) =2 / 5.
C. P(X=0) =(3/5)⁵. Vrai.
Probabilité de tirer un tube noncontaminé = 75 /(50 +75) = 3 / 5. P(X=0) =(3/5)⁵.
D. P(X=0) > P(X=2).

QCM 8.
Le domaine de définition de la fonction f définie par f(x) = ln(e^-x-2) est :
A. ]0 ; +oo[
e^-x-2 >0 ; e^-x > 2 ; 0,5 > e^x ; ln(0,5) > x ; -ln(2) > x
B. ] ln(2) ; + oo[
C. ] -oo ; - ln(2)[. Vrai.
D. ]0 ; 2[.

QCM 9.
Soit la fonction g définie sur IR par g(x)=(3-2x)e^-x . Une primitive de la fonction g est la fonction G définie sur IR par :
A. G(x) =(3x-x²)e^-x.
On dérive en posant u = 3x-x² et v = e^-x ; u' =3-2x ; v' = -e^-x ; u'v +v'u =e^-x(3-2x-3x+x²).
B. G(x) =(-3x+x²)e^-x.
On dérive en posant u = -3x+x² et v = e^-x ; u' = -3+2x ; v' = -e^-x ; u'v +v'u =e^-x(-3+2x+3x-x²).
C. G(x) =(2x-1)e^-x. Vrai.
On dérive en posant u = 2x-1 et v = e^-x ; u' = 2 ; v' = -e^-x ; u'v +v'u =e^-x(2-2x+1).
D. G(x) =(5-2x)e^-x.
On dérive en posant u = 5-2x et v = e^-x ; u' = -2 ; v' = -e^-x ; u'v +v'u =e^-x(-2+2x-5).

QCM 10.
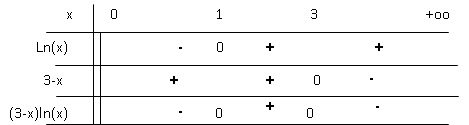
L’ensemble des solutions de l’inéquation ( 3-x) ln(x) > 0 sont :
A. [1 ; 3 ]. Vrai.
x doit être positif.

B. ]0 ; 3 ]
C. ] -oo ; 3 ]
D. [1 ; +oo[.

QCM 11.
L'intégrale suivante est égale à :
A. 1.
B. 0,5.
C. e / (2(1+e)).
D. ln[(1+e) / 2]. Vrai.

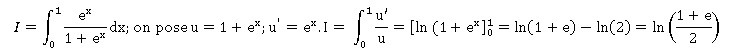
QCM 12.
Une variable aléatoire X suit la loi normale N(30, s² ) avec P(X >35)=0,4.
A. P(X < 30) = 0,4.
P(X < 30)=0,5. P(X < 35) = 0,6.
B. P(30 < X < 35)=0,1. Vrai.
C. P(25 < X < 35) =0,3.
D.P(X > 40) = 0,5..

....

Exercice 3.
On veut dépister une maladie m dont la fréquence (ou prévalence) dans la population P est notée p avec 0 < p < 1. On met en place un test diagnostique qui est indépendant de la valeur de p.
On prélève au hasard dans la population P un individu ayant été soumis au test diagnostique.
On définit les événements suivants :
T : « le test est positif » et M : « l’individu est malade ».
Pour ce test diagnostique, le fabricant a indiqué :
 la probabilité P_M(T) qu’un individu ait un test positif sachant qu’il est malade, est appelée sensibilité du test et est notée S_e.
 La probabilité P_{non M}(non T) qu’un individu ait un test négatif sachant qu’il n’est pas malade, est appelée spécificité du test et est notée S_p .
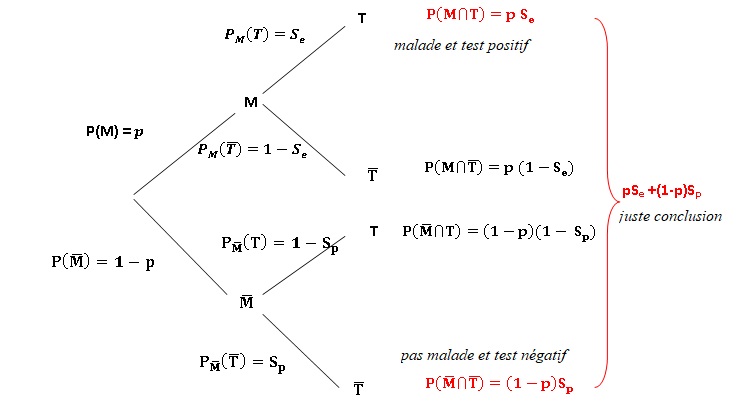
1) Illustrer la situation par un arbre pondéré en complétant toutes les branches à l’aide de p, S_e , S_p.
2) a) Exprimer P(M n T), P(M n non T), P(non M n T), P(nonM n non T) à l’aide de p, S_e et S_p.
b) Montrer que la probabilité que le test délivre une juste conclusion est : p(S_e-S_p) +S_p.

3) On appelle :
 Valeur prédictive positive du test (VPP), la probabilité P_T(M) d’être malade, sachant que le test est positif.
 Valeur prédictive négative du test (VPN), la probabilitéP_{non T} (non M) d’être non malade, sachant que le test est négatif.
a) Calculer P(T) à l’aide de p, S_e et S_p.
P(T) = pS_e + (1-p)(1-S_p).
b) Exprimer VPP et VPN en fonction de p, S_e et S_p.
VPP = P(T n M) / P(T) = pS_e / [pS_e + (1-p)(1-S_p)].
VPN = P(non T n non M) / P(non T) =(1-p)S_p / [p(1-S_e) +(1-p)S_p ] .
c) Le test est considéré comme intéressant si VPP > p. Montrer alors que : S_e+S_p > 1.
.pS_e / [pS_e + (1-p)(1-S_p)] > p ; S_e / [pS_e + (1-p)(1-S_p)] > 1.
S_e > [pS_e + (1-p)(1-S_p) ; (1-p) S_e > (1-p)(1-S_p) ; S_e > 1 -S_p; S_e+S_p > 1.
4) La prévalence p du paludisme est de 90 % en Tanzanie et de 0,001 en France.
Le test biologique utilisé a pour sensibilité S_e = 0,9 et pour spécificité S_p=0,8. Cela est valable pour toute la question 4.
a) Calculer la VPP en Tanzanie arrondie à 10^-2 près.
VPP= pS_e / [pS_e + (1-p)(1-S_p)]. =0,9 x0,9 / (0,9 x0,9+0,1 x0,2)=0,98.
On admet que VPP_France = 0 ; VPN_France = 1 ; VPN_Tanzanie= 0,47.
b) En déduire ce que l’on peut dire en terme de probabilité à un patient de Tanzanie et à un patient français selon que le test est positif ou négatif.
En France : Si le test est positif, vous êtes malade. Si le test est négatif, vous n'êtes pas malade.
En Tanzanie : Si le test est positif, il y a 98 chances sur 100 dêtre malade.. Si le test est négatif, il y a 47 chances sur 100 de ne pas être malade.
c) On considère la fonction v définie par v(p)= P_T(M).
i) Donner l’expression de v(p) en fonction de p,
v =VPP = P(T n M) / P(T) = pS_e / [pS_e + (1-p)(1-S_p)].
ii) Donner le sens de variation de la fonction v(p).
Dériver v(p) par rapport à p en posant u = pS_e et v = pS_e + (1-p)(1-S_p) ; u' = S_e ; v' = S_e-1+S_p.
(u'v -v'u) / v² = [S_e(pS_e + (1-p)(1-S_p)) -(S_e-1+S_p)pS_e] / v².
Le signe de la dérivée est celui de son numérateur.
0,9 (0,9 p+(1-p)x0,2) - (0,9-1+0,8)x0,9p=0,18.
La dérivée étant positive, v(p) est croissante.
iii) Lorsque p est supérieur à 0,8, en quoi la positivité du test est-elle un élément important du diagnostic ?
VPP est supérieur à 0,95. Si le test est positif, on a plus de 95 chances sur 100 d'être malade.

.

menu