Transformation
d'énergie dans une centrale nucléaire, Concours ITPE 2019.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
......
.....
|
Troisième partie.
Nous supposerons les mouvements non relativistes.
Un réacteur à neutrons thermiques utilise un modérateur pour ralentir
les neutrons issus des réactions de fission. Ce ralentissement
permet aux neutrons d'interagir avec les atomes fissiles ( uranium 235
ou plutonium 239 ) présents dans le combustible d'un réacteur
nucléaire. Lorsqu'un atome fissile se brise après absorption d'un
neutron thermique, il émet deux ou trois neutrons rapides possédant une
vitesse de l'ordre de20 000 km / s. A cette vitesse, il est peu
probable qu'un autre atme fissile absorbe ce neutron.
21. Calculer en joule l'énergie cinétique d'un neutron thermique. Mneutron = mn =1,37 10-27 kg.
E=0,025 eV =0,025 x1,60 10-19 = 4,0 10-21 J.
22. Quelle est la fréquence correspondant à un photon de même énergie que ce neutron ?
E = h n ; n = E / h = 4 10-21 / (6,63 10-34) ~6,03 1012 Hz.
23. Déterminer la longueur d'onde associée à cette fréquence. Dans quel domaine du spctre électromagnétique se situe t-elle ?
l = c / n = 3,00 108 / (6,03 1012) = 4,97 10-5 m.
Ce photon appartient au domaine infrarouge.
24. Expliquer l'appellation neutron thermique
Le rayonnement infrarouge transporte de l'énergie sous forme thermique.
Le neutron thermique ( ou neutron lent) a une énergie cinétique inférieure à 0,025 eV et une vitesse inférieure à 2 200 m /s.
25. Calculer la vitesse d'un neutron thermique.
½mnv2 = 4,0 10-21 ; v2 = 2 x4,0 10-21 / (1,67 10-27) = 4,79 106 ; v ~2,2 103 m / s ou 2,2 km /s.
26. Justifier l'expression neutron rapide.
Un neutron rapide a une énergie supérieure à 1 MeV et une vitesse supérieure à 14 000 km /s.
27. Enoncer la relation de Louis de Broglie reliant la quantité de mouvement p d'une particule matérielle, la longueur d'onde lDB associée et la constante de Planck h.
p = h /lDB.
28. Montrer la relation suivante : lDB = h / (2mnEc)½ en expliquant la signification de Ec.
p = mn v ; énergie cinétique du neutron thermique : Ec = 0,5 mnv2.
v = (2Ec / mn)½ ; mn v = (2mnEc)½; lDB = h / p = h /(2mnEc)½.
29. Déterminer numériquement lDB pour un neutron thermique.
lDB = h / (2mnEc)½ = 6,63 10-34 / (2 x1,67 10-27 x4 10-21)½ =1,8 10-10 m.
30. Justifier en trois lignes maximum la phrase suivante.
"Le neutron rapide va pour l'essentiel en ligne droite et sort
rapidement du coeur du réacteur, tandis que le neutron thermique
effectue un mouvement aléatoire lui donnant une trajectoire plus longue."
Les
neutrons rapides sont difficilement capturés par les noyaux,
contrairement aux neutrons lents.. La probabilité d'interaction diminue
lorsque l'énergie de la particule ( neutrons) augmente.
La quantité d'énergie est libérée lors de la fission, de l'ordre de 200 MeV pour un noyau d'uranium.
31. Quelle est la
quantité d'énergie libérée lors de la fission d'un kilogramme d'uranium
enrichi ( 3 à 4 % d'uranium 235, le seul fissile ) ? Exprimer cette
quantité en tep.
Pour 3 % d'uranium 235, soit 0,030 kg dans un kilogramme d'uranium enrichi.
Masse d'un noyau d'uranium 235 : mu =3,9 10-25 kg.
Nombre de noyaux d'uranium 235 : 0,030 / (3,9 10-25) =7,7 1022.
Energie libérée : 7,7 1022 x200 = 1,54 1025 MeV.
1,54 1025 x 1,6 10-13 ~2,5 1012 J = 2,5 103 GJ.
1 tep = 41,9 GJ ; 2,5 103 / 41,9 ~59 tep.
|
...
|
|
Quatrième partie : conversion en énergie mécanique.
L'énergie
libérée par réaction nucléaiire est convertie en énergie mécanique. De
l'eau est vaporisée par apport d'énergie due à la réaction nucléaire.
La détente de cette vapeur d'eau sous pression met en rotation la
turbine, puis le cycle se poursuit pour que l'eau soit de nouveau
vaporisée. Ce cycle de base, le cycle de Rankine, sera étudié.
On considérera toutes les transformations réversibles.
32. Exprimer
l'enthalpie massique h d'un fluide en fonction de son énergie massique
interne u, de la pression P et de son volume massique 1 / µ.
h = u + P / µ.
33. On considére le
cas où le fluide est un corps pur diphasé, à l'équilibre à la
température T, composé d'une phase liquide et d'une phase vapeur et on
note x la fraction massique de la vapeur. Exprimer l'enthalpie massique
h du système en fonction de x, de l'enthalpie massique de l'eau liquide
hL(T) et de l'enthalpie massique de l'eau vapeur hv(T).
h = (1-x) hL(T) + x hv(T).
On considère un fluide quelconque s'écoulant de façon permanente dans
une conduite, depuis la section d'entrée où toutes les grandeurs sont
indicées "e" jusqu'à la section de sortie où toutes les grandeurs
sont indicées "s".
On note he, Pe, Te et µe les enthalpie, pression, température et masse volumique à l'entrée de la conduite et hs, Ps, Ts et µs en sortie. Les variations d'énergies cinétique et potentielle seront négligées.
34. Faire une figure en y ajoutant l'entrée, la sortie, le sens d'écoulement et les enthalpies d'enntrée et de sortie.
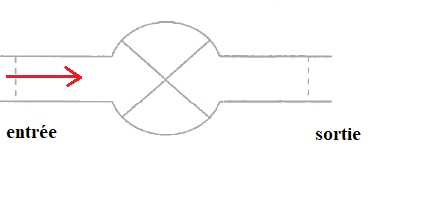
Au centre du dispositif, le renflement marqué d'une croix représente là où le fluide peut recevoir un travail massique utile wu ( autre que celui des forces de pression et entrée et sortie ) et une chaleur massique qth. La somme de ces transferts énergétiques correspond à la variation d'enthalpie massique lors de la traversée du dispositif.
35. Exprimer hs-he en fonction de wu et qth.
hs-he = wu + qth.
36. Si le fluide évolue de façon adiabatique, que représente hs-he ?
Lors d'une évolution adiabatique, qth est nulle et hs-he représente le travail utile wu.
37. Si le fluide s'écoule dans un échangeur thermique dans lequel il n'échange aucun travail utile, que représente hs-he ?
wu = 0 ; hs-he = qth, chaleur massique.
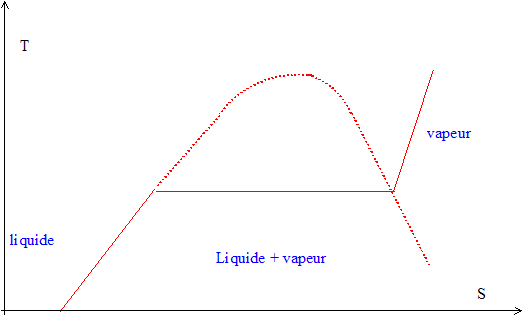
Le diagramme entropique de l'eau, ou diagramme ( T, s), représente
l'évolution de la température en fonction de l'entropie au cours de
transformations isobares. Les tirets marquent la courbe de saturation
qui limite le domaine où existent liquide et vapeur à l'équilibre. Les
pointillés fins sont les courbes pour lesquelles la fraction massique x
de la vapeur est constante. Le rectangle ABCD en trait plei représente
le cycle de Carnot qui sera étudié en fin de sujet.
38. Reproduire la
figure et y placer les domaines d'existence de la phase gazeuse, celle
de la phase liquide et le domaine de coexistence du liquide et de la
vapeur.
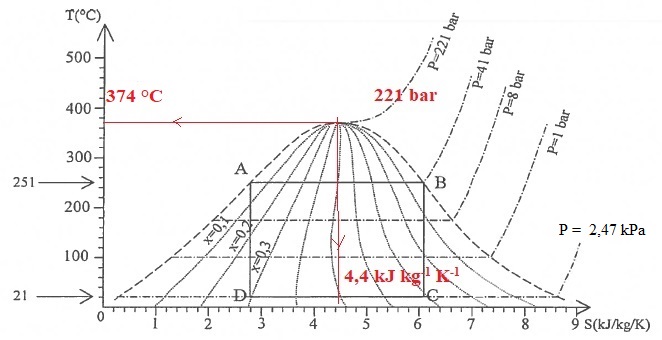
39. Donner la température, la presion et l'entropie massique du point critique de l'eau.
On considère le cas où le fluide est un corps pur diphasé, à
l'équilibre à la température T, composé d'une phase liquide et d'une
phase vapeur et on note x la fraction massique de la vapeur.
40. Quelle est dans ce cas la valeur maximale pour T ?
374 K.
41. Exprimer l'entropie massique s du système en fonction de x, de l'entropie massique de l'eau liquide sL(T) et de l'entropie massique de l'eau vapeur sv(T).
s = (1-x) sL(T) + x sv(T).
42.
En considèrant la vaporisation complète d'un kilogramme d'eau dans un
échangeur thermique dont l'état initial est liquide saturant et l'état
final vapeur saturante; donner une relation entre hL(T), hv(T), sL(T), sv(T) et T.
hv(T) -hL(T) = T [sv(T) -sL(T) ].
43. Exxprimer sL(T) puis calculer sa valeur à 21 °C.
On donne à 21°C : P =2,47 kPa ; hL = 87,5 kJ kg-1 ; hv = 2540 kJ kg-1 ; sv = 8,65 kJ kg-1 K-1.
sL(T) = - [
hv(T) -hL(T) ] / T + sv(T) = - (2540 -87,5) / (273 +21) + 8,65 ~0,308 kJ kg-1 K-1 |
....
|
Installation motrice à vapeur.
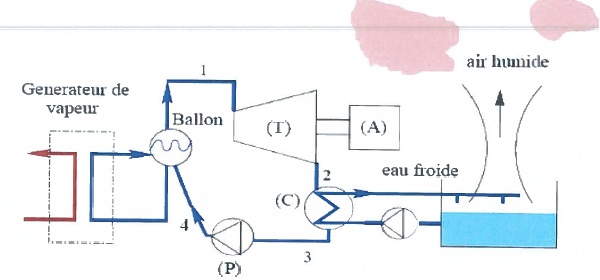
Le générateur de vapeur, dans lequel le fluide, ici l'eau, est transformé en vapeur.
L'eau diphasique n'est pas totalement vaporisée, mais les phases vapeur
et liquide sont séparées par gravité dans le ballon de sorte que le
fluide en 1 soit bien de la vapeur saturante.
La transformation de l'eau de 4 à 1 dans le générateur de vapeur et le ballon est isobare à 41 bar.
La turbine T dans laquelle la vapeur se détend de la haute pression à la basse pression, de façon adiabatique réversible.
Le condenseur C où l'eau se condense par échange de chaleur avec le fluide froid provenant d'un fleuve par exemple.
Une pompe P remet alors le fluide dans l'état liquide saturant à 41
bar, de façon adiabatique réversible. La puissance nécessaire à son
fonctionnement est prélevée directement sur l'arbre de l'alternateur.
44. Quel est l'état
du fluide aux points A, B, C et D. On précisera à chaque fois la
température, la pression et les fractions massiques en vapeur et en
liquide.
Point A : liquide saturant, 251 °C, 41 bar, x = 0.
Point B : vapeur saturante, 251 °C, 41 bar, x = 1.
Point C : liquide + vapeur, 21 °C, P = 2,47 kPa, x = 0,7.
Point D : liquide + vapeur, 21 °C, P = 2,47 kPa, x = 0,3.
45. Associer à ces points le numéro correspondant de la figure.
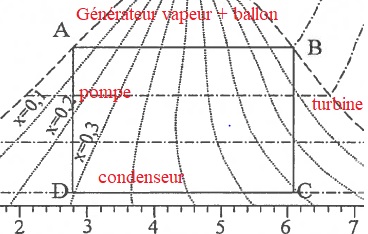
Sortie du ballon, entrée de la turbine ( point B) ; sortie de la turbine, entrée du condenseur ( point C) ;
sortie du condenseur, entrée de la pompe ( point D) ; sortie de la pompe ( point A).
46. Associer à chaque segment un élément de l'installation.
Segment 1 : du ballon vers la turbine T.
Segment 2 : de la turbine T vers le condenseur C .
Segment 3 : du condenseur C ( point D) vers la pompe P.
Segment 4 : de la pompe P vers le ballon.
47. Calculer le transfert thermique qth GV effectué dans le générateur de vapeur, le transfert thermique qth C effectué dans le condenseur et le transfert thermique qth total effectué sur l'ensemble du cycle.
D --> A ( pompe) : adiabatique réversible, pas de transfert thermique.
C --> D ( condenseur) isobare, qth C = T(sL-sv)( xC-xD)=(273 + 21) (0,308-8,65)x(0,7-0,3) = -0,981 MJ kg-1.
B --> C ( turbine) : adiabatique réversible, pas de transfert thermique.
A--> B : (générateur de vapeur) : isobare ;
à 251 °C, sv =6,07 kJ kg-1 K-1 ; sL = 2,81 kJ kg-1 K-1 ; qth GV = (273 + 251) (6,07-2,81) = 1,71 MJ kg-1.
qth total = 1,71 -0,981= 0,729 MJ kg-1.
48. Donner la variation d'enthalpie sur un cycle et en déduire le travail utile sur un cycle wu total.
Sur le cycle, la variation d'enthalpie est nulle ( état final et état initial identiques ).
hs-he =0= wu total + qth total .
wu total = - qth total = -0,729 MJ kg-1.
49. Définir, exprimer en fonction des températures et calculer le rendement de Carnot pour ce cycle ABCD.
Rendement = |wu| / qth AB ;
Premier principe, sur le cycle : wu + qth total = 0 soit : wu = - qth total .
Second principe, sur le cycle : qth AB / TA + qth CD / TC = 0.
qth CD / qth AB = -TC / TA ;
rendement = (qth AB + qth CD) / qth AB =1-TC / TA = 1- (273+21) / 273 +221) =1-0,56 = 0,44.
50. Justifier l'utilisation d'eau pressurisée dans les installations motrices à vapeur.
L'eau doit rester liquide dans le coeur du réacteur. Pour cela l'eau doit être maintenue à une pression suffisamment élevée.
51. Comment le travail se manifestera t-il sur l'alternateur ?
Conversion d'énergie mécanique en grande partie en énergie électrique.
|
|




