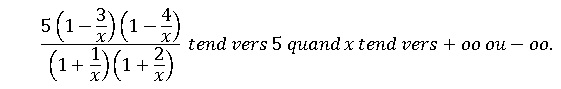Mathématiques,
concours audioprothésiste Toulouse 2019.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
......
.....
|
QCM 1. Dans un repère rapporté à un repère orthonormé, on donne les points :
A(1 ; 1 ; -2) ; B ( 3 ; 1 ; 0) ; C(4 ; 1 ; 1) ; D (6 ; 6 ; 2).
Indiquer si les propositions suivantes sont vraies ou fausses.

QCM 2. Soit r un nombre rél donné. On considère les deux suites suivantes :
un = rn ; Sn = 1 +r +r2 +r3 +...+rn pour n > 0.
Indiquer si les propositions suivantes sont vraies ou fausses.
A. Lorsque |r| < 1, la suite (un) converge vers zéro. Vrai.
par exemple si r = -0,1 et n =9 ; un = -10-9 ; ; un+1 =10-10.
B. Lorsque |r| = 1, la suite (un) converge vers 1. Faux.
Si r = 1, un = 1 ; si r = -1 et n pair, un = 1 mais un+1 = -1.
C. Pour r = 0,5, S3 = 2. Faux.
r0 = 1 ; r1 = 0,5 ; r2=0,52=0,25 ; r3=0,53=0,125 ; S3 = 1,875.
D. Pour r = 0,5 la suite vn = n rn tend vers plus l'infini quand n tend vers plus l'infini. Faux.
0,5n tend vers zéro et vn tend vers zéro.
E. Pour r = 3, la suite Sn tend vers plus l'infini quand n tens vers plus l'infini. Vrai.
QCM.3. Le plan complexe est muni d'un repère orthonormé direct.
On considère les points A, B et C d'affixes respectives :
a = 2 + 2 i 3½ ; b = 2 -2 i 3½ ; c = 4i.
Indiquer si les propositions suivantes sont vraies ou fausses.
A. Le module de a vaut 16. Faux.
(22 +(2x3½)2)½ = (4 +12)½ = 16½ = 4.
B. Les trois points sont situés sur un même cercle de centre O. Vrai.
OA = 4 ; |b|=(22 +(-2x3½)2)½ = (4 +12)½ = 16½ = 4 ; OC = |c| = 4.
C. Un argument de a vaut p/3. Vrai.
a / |a| = 0,5 + 0,5 i 3½ = cos (p/3 )+ i sin (p/3 ).
D. Le point B' d'affixe b' = b exp(i p/3) se situe sur l'axe vertical. Faux.
b = 4 (cos (-p/3 )+ i sin (-p/3 ) = 4 exp(-i p/3).
b' = 4 exp(i(- p/3 + p /3)) = 4.
E. Le milieu du segment [AB] se situe sur l'axe horizontal. Vrai.
(2+2) / 2 = 2 ; (2 i 3½ -2 i 3½ ) / 2 = 0.
QCM 4. Soient les nombres complexes suivants : z1 = 1-i ; z2 = 4+3i.
Indiquer si les propositions suivantes sont vraies ou fausses..
A. Un argument de z1 est p / 4. Faux.
|z1| = (12 +(-1)2))½ = 2½.
z1 / |z1| = 1 / 2½ - i / 2½ = cos(-p/4) + i sin(-p/4).
B. L'une des racines cubiques de z1 s'écrit z =21/6 exp(i 7 p / 12). Vrai.
z1 =2½exp ( - i p / 4).
L'une des racines cubiques de z1 est :: 21/6 exp(-i p / 12).
Mais aussi : 21/6 exp(-i (p / 12 +2p/3) ) et 21/6 exp(-i (p / 12 +4p/3) ).
C. Le nombre complexe conjugué de z2 est : -4-3i. Faux.
Conjugué de z2 : 4-3i
D. La partie réelle de z1 / z2 vaut -7 / 25. Faux.
z1 / z2 = (1-i)(4-3i) / [(4+3i)(4-3i)] = (4+3i2-7i) / (16 +9) = (1-7i) / 25.
E. La partie imaginaire de z1 / z2 vaut -7 / 25. Vrai.
|
...
|
|
QCM 5. On considère les deux fonctions suivantes : f(x) = sin(2x) et g(x) = cos(x) f(x) pout tout x réel..
Indiquer si les propositions suivantes sont vraies ou fausses.
A. L'ensemble des zéros de f est exactement l'ensemble { kp, k appartenant à Z }. Faux.
f(x) = 0 = sin (2x).
2x = 0 + 2kp ; x = kp ;
et 2x = p + 2kp ; x = ½p + kp.
B. L'ensemble des zéro de g est le même que l'ensemble des zéro de f. Vrai.
cos(x) = 0 ; x = ±p/2 + 2kp.
C. g est une fonction paire. Faux.
cos(x) est une fonction paire ; sin(2x) est impaire.
D. g'(x) = -sin(x) sin(2x) +cos(x) cos(2x). Vrai.
On pose u = sin(2x) et v = cos(x).
u' = 2 cos(2x) ; v' = -sin(x) ; u'v +v'u = 2 cos(2x) cos(x) -sin(x) sin(2x).
E. La fonction f(x) / g(x) est définie pour tout x réel. Faux.
f(x) / g(x) =1 / cos(x). Le dénominateur ne doit pas être nul.
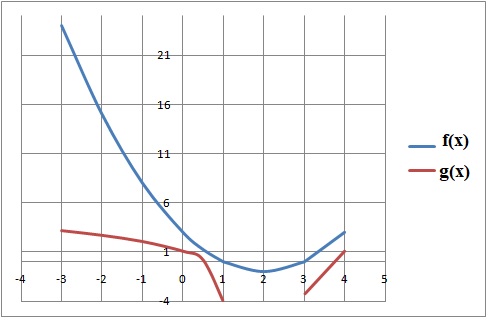
QCM 6. Soient deux fonctions f(x) = x2-4x+3 et g(x) = ln(f(x)).
Indiquer si les propositions suivantes sont vraies ou fausses.
A. f(x) admet deux racines réelles distinctes. Vrai.
Discriminant D = (-4)2 -4 x1 x3 = 4.
x1 =(4-2) / 2 = 1 et x2 = (4+2) / 2 = 3.
B. La fonction f est de signe constant sur R. Faux.
f '(x) = 2x-4 ; f '(x) = 0 si x =2.
f(2) = -1.
Sur ]-oo ; 2 [, f(x) décroit de +oo à -1 et sur [2 ; +oo[, f(x) croît de - 1 à + oo.
C. La fonction g est paire. Faux.
g(x) =ln(x2-4x+3) ; g(-x) = ln(x2 +4x +3) ; g(x) diffère de g(-x).
D Le domaine de définition de g est exactement l'ensemble ]-oo ; -3[ union ]-3 ; +oo[. Faux.
f(x) doit être strictement positive.
x doit appartenie à ]-oo ; 1[ union ]3 ; +oo[.
E. La dérivée g' de la fonction g vérifie la relation g'(x) f(x) = 2(x-2). Vrai.
g '(x) = f '(x) / f (x) ; g '(x) f(x) = f '(x) = 2x-4.
QCM 7. Soit la fonction f(x) = x2-x pour x > 0 et soit la suite (un) définie par u0 réel et un+1 = f(un) pour tout n > 0.
Indiquer si les propositions suivantes sont vraies ou fausses.
A. La fonction f s'annule en exactement deux points sur l'intervalle [0 ; +oo[. Vrai.
f(x) = x( x-1) ; f(x) s'annule pour x = 0 et x = 1.
B. La fonction f a un unique point fixe sur l'intervalle [0 ; +oo[.
C. Lorsque u0 = 2, la suite (un) est strictement croissante. Faux.
u1 =f(2) =2 ; u2 = f(2). La suite est constante.
D. La fonction g(x) = f(x) -x est strictement positive sur [3 ; +oo[. Vrai.
g(x) = x2-2x.
g '(x) = 2x-2 ; g'(x) = 0 si x =1.
g'(x) >0 sur [1 ; + oo[ ; g(x) est strictement croissante sur [3 ; +oo[.
E. Lorsque u0 = 3, la suite (un) est strictement croissante. Vrai.
u1 = f(3) = 9-3 = 6 ; u2 =f(6) = 36-6 = 30. La propriété est vraie au rang 1.
On suppose la propriété vraie au rang n : un+1 = f(un) =un2 -un ; un+1-un =g(un).
Or g(x) = f(x) -x est strictement positive sur [3 ; +oo[.
La propriété est vraie au rang un et héréditaire ; elle est vraie pour tout n.
|
....
|
QCM 8.
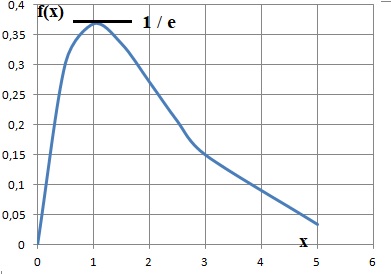
Soit la fonction f(x) = x e-x pour x >0.
Indiquer si les propositions suivantes sont vraies ou fausses.
A. La fonction f est décroissante sur [1 ; +oo[. Vrai.
On pose u =x et v = e-x ; u' = 1 et v' = -e-x ; u'v +v'u = e-x -x e-x = e-x(1-x).
La dérivée est négative ou nulle sur [1 ; +oo[.
f(x) est décroissante sur cet intervalle.
B. Quand x tend vers plus l'infini, f(x) tend vers l'infini. Faux.
Quand x tend vers plus l'infini, e-x tend vers zéro.
C. Pour tout x appartenant à [0 ; +oo[, on a : f(x) < 1 /e. Vrai.
f(1) = 1 /e.
f(x) croît de zéro à 1 /e puis décroît de 1 /e à zéro.
D. La fonction g(x) = ex[ f(x) + f '(x) ] tend vers 1 quand x tend vers plus l'infini. Vrai.
g(x) = ex[ x e-x + e-x(1-x) ] =e0=1
E. Une primitive de f est h(x) =-(x+1)e-x. Vrai.
On dérive h(x) en posant u = x+1 et v = - e-x ; u' = 1 ; v' = e-x ;
u'v + v' u = -e-x +e-x(x+1) =f(x).
QCM 9.
Soit la foncttion f(x) = 5(x-3)(x-4) / [(x+1)(x+2)].
Indiquer si les propositions suivantes sont vraies ou fausses.
A. La limite de f(x) en plus l'infini est égale à la limite de f(x) en moins l'infini. Vrai.
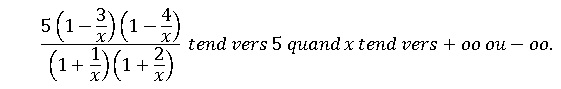
La droite y = 5 est asymptote.
B. Le graphe de la fonction f admet une asymptote horizontale. Vrai.
C. La droite x=-1 est une asymptote pour le graphe de f. Vrai.
D. Le graphe de la fonction f admet 4 asymptotes verticales qui sont les droites x =3 ; x = 4 ; x =-1 et x = -2. Faux.
Deux asymptotes verticales d'équation x = -1 et x = -2.
E. La fonction f est positive sur l'intervalle ]3 ; 4 [. Faux.
(x-3) est positif , (x-4) est négatif ; (x+1) est positif ; (x+2) est positif ; f est négative sur cet intervalle.
QCM 10. Indiquer si les propositions suivantyes sont vraies ou fausses.
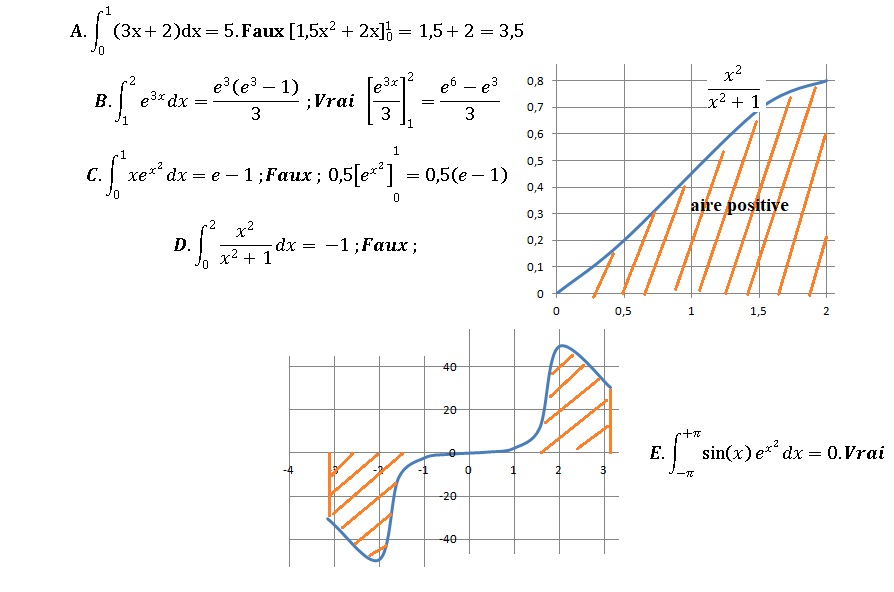
|
QCM 11. Dans une étude on évalue un nouvel examen clinique permettant de diagnostiquer une surdité. On note ::
S l'événement " avoir réellement une surdité".
non S l'événement " n'avoir aucune surdité en réalité".
E l'événement " avoir un examen clinique en faveur d'une surdité"
non E l'événement " avoir un examen clinique en faveur de l'absence de surdité".
Les résultats de l'étude sont les suivants, ils indiquent notamment que
l'examen clinique ne permet pas, avec certitude, de faire une
distinction entre les personnes ayant vraiment une surdité et les
personnes indemnes.
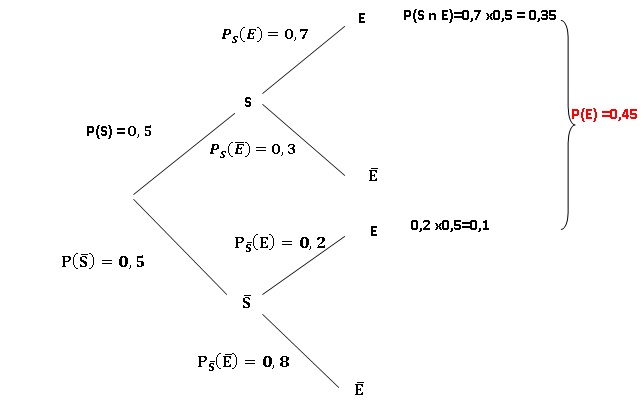
50 % de la population d'étude avait réellement une surdité P(S) = 0,50 ;
la probabilité d'avoir un examen clinique en faveur d'une surdité (E) chez les personnes réellement sourdes (S) était PS(E) = 0,70 ;
la probabilité d'avoir un examen clinique en faveur de l'absence de
surdité ( non E) chez les personnes réellement indemnes ( non S) était Pnon S ( non E) = 0,80.
Indiquer si les propositions suivantes sont vraies ou fausses.
A. La probabilité de n'avoir aucune surdité en réalité est P(non S) = 0,50. Vrai.
B. La
probabilité d'avoir un examen clinique en faveur d'une surdité, sachant
que la personne est réellement indemne de surdité est P non S(E) = 0,30. Faux.
C. La probabilité d'avoir à la fois une surdité réelle et un examen clinique en faveur d'une surdité est P(S n E) = 0,35. Vrai.
C. La probabilité d'avoir un examen clinique en faveur d'une surdité est P(S n E) = 0,35. Vrai.
D. La probabilité d'avoir un examen clinique en faveur d'une surdité est P(E) = 0,55. Faux.
E. La probabilité d'avoir réellement une surdité sachant que l'examen clinique est en faveur d'une surdité est PE(S) = 0,35 / 0,45. Vrai.
QCM 12. On
s'intéresse à une population de patients atteints de surdité, composée
d'hommes et de femmes. La surdité peut être d'origine traumatique ou
non traumatique. Dans cette population :
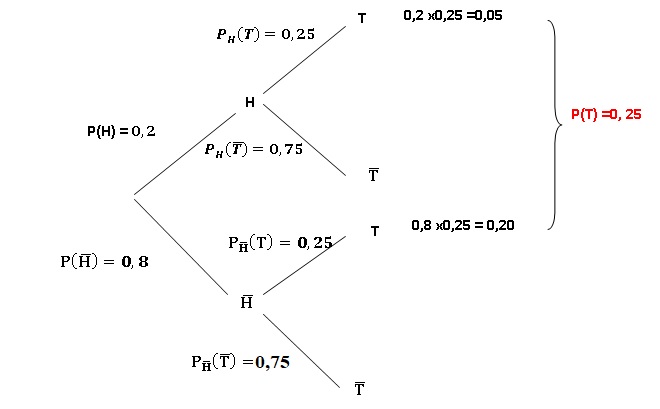
la probabilité d'être un homme est P(H) = 0,20 ;
la probabilité d'avoir une surdité d'origine traumatique est P(T) = 0,25 ;
la probabilité être un homme et d'avoir une surdité d'origine traumatique est P(H n T) = 0,05.
Indiquer si les propositions suivantes sont vraies ou fausses.
A. La probabilité d'être un homme ou d'avoir une surdité d'origine traumatique est P(H u T) = 0,45. Faux.
P(H) + P(T) -P(H nT) = 0,2 +0,25 -0,05 = 0,40.
B. Les événements " être un homme" et "avoir une surdité d'origine traumatique" sont indépendants. Vrai.
P(H n T ) = 0,05 ; P(H) xP(T) =0,2 x0,25 =0,05.
C. la probabilité d'avoir une surdité d'origine traumatique chez les hommes est PH(T) = 0,20. Faux.
D. La probabilité de ne pas avoir de surdité d'origine traumatique chez les hommes est PH(non T) = 0,75. Vrai.
E. Les événements " ne pas être un homme" et " ne pas avoir de surdité d'origine traumatique" sont incompatibles. Faux.
|
|
|