Physique
chimie, mathématiques, concours Aspts Nord
2019.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
Exercice 1. 4 points.
On donne le programme de calcul suivant :
Choisir un nombre.
a) Multiplier ce nombre par 3.
b) Ajouter le carré du nombre choisi.
c) Multiplier le tout par 2.
Écrire le résultat.
1. 1.Montrer que, si on choisit le nombre 10, le résultat obtenu est 260.
10 x3 =30 ; 30 +102=130 ; 130 x2 =260.
2. Calculer la valeur exacte du résultat obtenu lorsque :
• le nombre choisi est −5.
-5 x3 = -15 ; -15 +(-5)2= -15+25=10 ; 10 x2 =20.
• le nombre choisi est 2 / 3.
2 / 3 x 3 =2 ; 2 +4 /9 =18 /9 +4 /9 =22 /9 ; 22 /9 x2 = 44 / 9.
3. Donner l’expression obtenue lorsque l’on choisit x.
3 x ; 3x +x2 ; 2(3x +x2).
Exercice 2. 5 points.
On donne la feuille de calcul ci-dessous.
La colonne B donne les valeurs de l’expression 2x 2 − 3x − 9 pour quelques valeurs de x de la colonne A.
1. Si on tape le nombre 6 dans la cellule A17, quelle valeur va t-on obtenir dans la cellule B17 ?
2 *62 -3*6-9 =72-18-9=45
|
A
|
B
|
|
x
|
2x 2 − 3x − 9
|
1
|
-2,5
|
11
|
2
|
-2
|
5
|
3
|
-1,5
|
0
|
4
|
-1
|
-4
|
5
|
-0,5
|
-7
|
6
|
0
|
-9
|
7
|
0,5
|
-9
|
8
|
1
|
-10
|
9
|
1,5
|
-9
|
10
|
2
|
-7
|
11
|
2,5
|
-4
|
12
|
3
|
0
|
13
|
3,5
|
5
|
14
|
4
|
11
|
15
|
4,5
|
18
|
16
|
5
|
26
|
2. A l’aide du tableur, trouver deux solutions de l’équation 2x 2 − 3x − 9 = 0.
-1,5 et 3.
3. L’unité de longueur est le cm.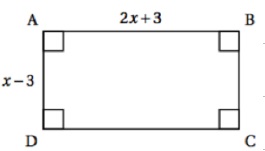
a. Montrer que l’aire du rectangle ci-contre vaut 2x 2 − 3x − 9.
Longueur fois largeur =(2x+3) (x-3)= 2x2-6x+3x-9 =2x 2 − 3x − 9.
b. Donner une valeur de x pour laquelle l’aire du rectangle vaut 5 cm2. Justifier.
Ligne 13 du tableur : x = 3,5.
Ou bien 2x 2 − 3x − 9 =5 ; 2x 2 − 3x − 14 =0 ;
discriminant : (-3)2 -4 *2*(-14) =121 ; 121½ =11 ; solution retenue : (3 +11) / 4 =3,5.
c. Pourquoi ici x ne peut-il être égal à 2,5 ?
La longueur et la largeur du rectangle doivent être positives.
Exercice 3. 4 points.
Toutes les réponses doivent être justifiées.
Un tasseau est un morceau de bois en forme de parallélépipède rectangle.
Le père de Tom lui a fourni sept tasseaux représentés ci-dessous avec leur longueur respective exprimée en mètre.
Tom les a numérotés de 1 à 7 :
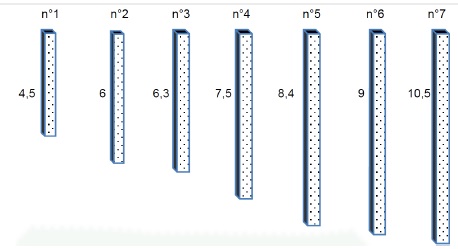
Par la suite on considère les tasseaux comme des segments.
PARTIE I.
Le père de Tom lui a demandé de choisir des tasseaux pour construire des triangles rectangles.
1. Tom a choisi les tasseaux n°1, n°2 qu’il a disposés en angle droit comme ci-dessous :

Démontrez qu’il possède un tasseau pour satisfaire la demande de son père.
Th. de Pythagore : 4,52 +62=56,25 ; prendre la racine carrée : 7,5 ( n° 4).
2. Aidez Tom à trouver 3 autres tasseaux qui répondent à la demande de son père.
n°2 ; n°5 ; n° 7.
PARTIE II.
Sur le schéma ci-dessous Tom a disposé 4 tasseaux et a pris soin que le n°1 et le n°3 soient parallèles.
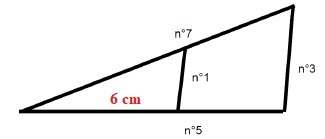
A l’aide du Théorème de Thalès,calculez où se trouve le tasseau n°1 sur le tasseau n°5.
Rapport entre les côtés du grand et du petit triangle : n°3 / n°1 soit 6,3 / 4,5 =1,4.
8,4 /1,4 =6
Exercice 4 : ( 4 points)
Le
professeur choisit trois nombres entiers relatifs consécutifs rangés
dans l’ordre croissant. Leslie calcule le produit du troisième nombre
par le double du premier. Jonathan calcule le carré du deuxième nombre
puis il ajoute 2 au résultat obtenu.
1. Leslie a écrit le calcul suivant :11×(2×9). Jonathan a écrit le calcul suivant : 102+2
a. Effectuer les calculs précédents.
11 x2 x9 = 198 ; 102+2 = 102.
2. Le professeur choisit maintenant trois nouveaux entiers. Leslie et Jonathan obtiennent alors tous les deux le même résultat.
a. Le professeur a-t-il choisi 6 comme deuxième nombre ?
62+2 =38 ; 7 x(2 x 5)=17 différe de 38. Le professeur n'a pas choisi 6 comme second nombre..
b. Le professeur a-t-il choisi−7 comme deuxième nombre ?
(-7)2+2 =51 ; -6 x(2 x (-8))=96 différe de 51. Le professeur n'a pas choisi -7 comme second nombre..
c. Arthur prétend qu’en prenant pour inconnue le deuxième nombre entier (qu’il appelle n), l’équation n2
=4 permet de retrouver le ou les nombres choisis par le professeur.
A-t-il raison? Justifiez votre réponse en expliquant comment il a
trouvé cette équation, puis
donner les valeurs possibles des entiers choisis.
Arthur : n2 +2 ; Leslie : (n+1) x2x (n-1) = 2(n2-1).
n2 +2 =2(n2-1) ; n2=4. n =±2.
Exercice 5. 3 points.
Cet exercice est un questionnaire à choix multiple. Aucune
justification n’est demandée. Pour chacune des questions, une seule
réponse est exacte. Entourez la réponse exacte.
6-4(x-2) est égal à : 2x-4 ; 14-4x ; 6-4x-2 ; -2-4x.
2 x10-3 x10-5 est égal à :2 x10-15 ; 2 x102 ; 2 x 10-8 ; 0,02.
Pour x = -2, l'expression 5x2+2x-3 est égale à : 13 ; -27 ; 17 ; -19.
|
|
|
Physique chimie.
Exercice 1 : (2 points)
Jean possède une bille métallique. Il souhaite connaître la densité du métal dont est constituée cette bille.
a. Pour déterminer
le volume de la bille, Jean la plonge dans une éprouvette graduée
contenant 30 mL d’eau. Il lit la nouvelle graduation atteinte par l’eau
: 44,1 mL. En déduire le volume de la bille.
V = 44,1 -30 = 14,1 mL.
b. Jean mesure une masse de 100,1 g. Calculer la masse volumique du métal constituant la bille.
100,1 / 14,1 ~7,1 g / mL.
Exercice 2 : (2 points)
Quel risque représente ce pictogramme ? 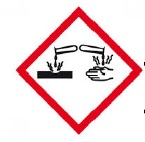
Qu’est-ce que cela signifie ?
Produit corrosif. Peut endommager les tissus humains, les métaux, le bois.
Un stylo posé immobile sur une table est soumis :
- à deux forces qui se compensent : la réaction de la table sur le stylo et le poids du stylo. Vrai.
- à une seule force : la réaction de la table sur le stylo. Faux.
- à une seule force : le poids du stylo. Faux.
Dans un circuit comportant une dérivation, l’intensité du courant dans la branche principale est :
- égale au produit des intensités dans les deux autres branches. Faux.
- la même que celle circulant dans les deux branches dérivées. Faux.
- égale à la somme des intensités dans les deux autres branches. Vrai.
Exercice 3. 2 points..
Les
éoliennes offshore (en pleine mer) peuvent fournir une puissance de 6
MW(mégaWatt) par heure (contre 2MW/h pour les éoliennes terrestres), et
peuvent fonctionner environ 2500 heures par an.
a. Calculer l’énergie produite par une éolienne offshore en un an.
6 x 2500 =1,5 104 MWh = 1,5 1010 Wh..
b. Combien
d’éoliennes offshore faudrait-il pour produire l’énergie électrique
annuelle de 20TWh consommée en Bretagne ? (1TWh = 1012 Wh).
20 x1012 / (1,5 1010) ~1334.
Exercice 4. (9 points)
Le véhicule hybride est l’une des solutions développées par certains
constructeurs automobiles pour réduire l’émission de gaz à effet de
serre, dans le cadre de leur contribution à la protection de
l’environnement.
Le véhicule hybride est équipé de deux moteurs :
- un moteur à combustion consommant du carburant (essence ou fuel) ;
- un moteur électrique alimenté par une batterie rechargeable.
Quand la batterie est suffisamment chargée, le moteur électrique peut
assurer seul la propulsion du véhicule (avec une autonomie de plusieurs
dizaines de kilomètres)/
Dans le cas contraire, les deux moteurs fonctionnent simultanément. Le
moteur électrique accompagne le moteur thermique pour lui permettre de
consommer moins de carburant.
1. Identifier la source d’énergie utilisée par le moteur à combustion.
fuel, essence.
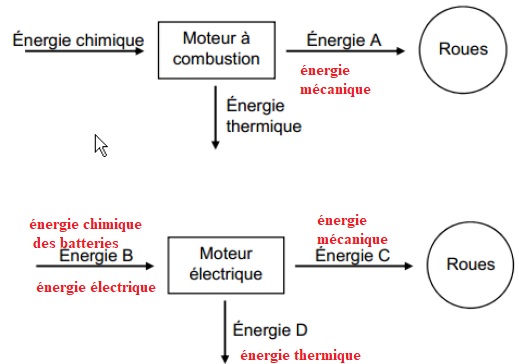
2. Les diagrammes
énergétiques simplifiés permettant de schématiser les transformations
d’énergie dans les moteurs à combustion et électrique sont les suivants
:
Nommer les énergies A, B, C et D.
3.
Grâce à un système régénératif, la batterie du véhicule hybride se
recharge lors des phases de freinage. Une partie de l’énergie cinétique
du véhicule est alors récupérée et transformée en énergie électrique.
On considère la situation de freinage suivante.
Un véhicule hybride de 1 300 kg se déplace en ville à la vitesse de 50 km/h et freine pour s’arrêter au stop.
3.1. Vérifier que l’énergie cinétique du véhicule avant freinage vaut 125 kJ.
v = 50 /3,6~13,9 m /s.
Energie cinétique = ½mv2 = 0,5 x1300 x13,92 ~125 386 J ~125 kJ.
3.2. Au cours de ce freinage, 60 % de l’énergie cinétique récupérée est transformée en énergie électrique.
Déterminer le nombre de freinages (supposés tous identiques à cette
situation ) qui sont nécessaires pour recharger totalement une batterie
dont la capacité énergétique est de 1,3 kWh, soit 4680 kJ.
Energie électrique :125 x0,6 =75 kJ par freinage.
Nombre de freinage : 4680 / 75 =62,4.
4.
En déduire pourquoi un véhicule hybride est davantage destiné à la
circulation urbaine qu’à la circulation sur autoroute ou voie rapide.
En ville : faible distance parcourue et nombreux freinages.
Sur autoroute : grande distance parcourue et peu de freinage.
5.
Une voiture de 600 kg roule à 50 km/h. Un animal surgit sur la route à
200 m de la voiture. Le conducteur met 1,1 seconde à réagir avant
d’appuyer sur le frein. Déterminer la distance parcourue par la voiture
pendant le temps de réaction du conducteur, notée Dr.
v = 50 / 3,6 ~13,9 m /s.
Dr = 13,9 x1,1 ~ 15,3 m.
6. La distance d’arrêt notée Da
du véhicule (distance parcourue par le véhicule entre le moment où le
conducteur aperçoit un obstacle et le moment où le véhicule s’arrête)
est la somme de la distance de réaction notée Dr et la distance de freinage notée Df.
La distance de freinage d’un véhicule bien entretenu roulant sur une route sèche à une vitesse de 50 km/h est de 16 m.
Exprimer Da en fonction de Dr et Df puis calculer la distance d’arrêt d’un véhicule roulant à une vitesse de 50 km/h.
Da = Dr + Df = 15,3 +16 = 31,3 m.
|
|
|
|
Exercice 5. 5 points.
Les quatre métaux les plus couramment utilisés sur un chantier, pendant
la construction d’un bâtiment, sont le cuivre, le fer, le zinc, et
l’aluminium. Afin de mieux connaître ces métaux, un bureau d’étude
dispose de quatre cylindres A, B, C et D de même volume .
Il dispose également d’un tableau de données donnant la masse des
cylindres et la température de fusion des métaux qui les constituent.
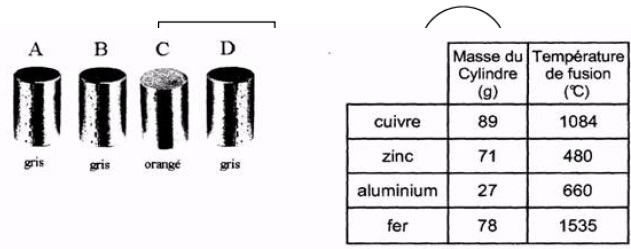
1. Les quatre cylindres (A, B, C, D) ont été mélangés.
1.1. Indiquer la nature du métal dont est constitué le cylindre C. Expliquer la réponse.
Couleur orangé : cuivre. Les autres métaux sont gris.
1.2. On approche un aimant de chacun des cylindres. Seul le cylindre D est attiré par l’aimant.
Indiquer la nature du métal dont est constitué le cylindre D.
Seul le fer est attiré par l'aimant. Cuivre, zinc, aluminium ne le sont pas.
1.3. Sachant que la masse du cylindre B est plus petite que celle du cylindre A, et en utilisant les
données, compléter le tableau suivant.
Cylindre
|
Métal
|
A
|
zinc
|
B
|
aluminium
|
2. On étudie l’action d’un décapant acide, utilisé sur un chantier, sur un morceau de fer.
2.1. Nommer l’appareil permettant de mesurer le pH d’une solution.
Le pHmètre.
2.2. Entourer la valeur qui correspond au pH de la solution décapante. Expliquer le choix. 2 ; 7 ; 12.
Une solution acide a un pH inférieur à 7.
3. On plonge un clou en fer
dans un tube à essais contenant du décapant. On observe un dégagement
gazeux. On présente alors une flamme à l’entrée du tube et une
détonation se produit.
3.1. Donner le nom et la formule chimique du gaz mis en évidence.
Dihydrogène H2.
3.2. Légender le schéma ci-après :
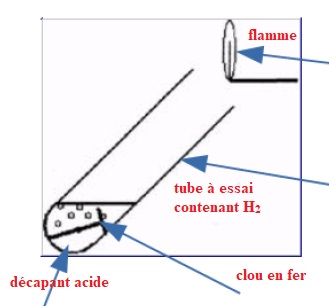
|
|
|