Mathématiques,
bac S Antilles 2020.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
..
..
|
.
.
|
..
..
......
...
|
Exercice
1. 6 points.
Partie A.
Louise se rend au travail avec sa voiture. Sa collègue Zoé ne possède
pas de voiture. Chaque matin, Louise propose à Zoé de l'emmener. Quelle
que soit la réponse de Zoé, Louise lui propose de la ramener le soir.
La probabilité que Louise emmène Zoé le matin est 0,55.
Si Louise a emmené Zoé le matin, la probabilité qu'elle la ramène le soir est 0,7.
Si Louise n'a pas emmené Zoé le matin, la probabilité qu'elle la ramène le soir est 0,24.
On note M et S les événements suivants :
M : "Louise emmène Zoé le matin".
S: " Louise ramène Zoé le soir".
1. Construire un arbre pondéré traduisant la situation.
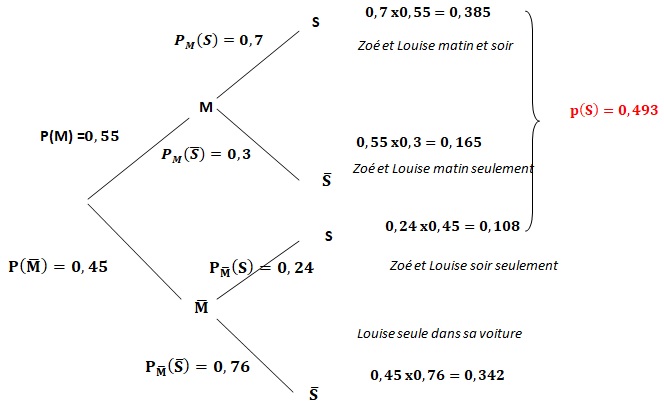
2. Calculer P(M n S) et traduire ce résultat par une phrase.
P(M n S) =0,55 x 0,7 =0,385.
La probabilité que Louise emmène Zoé matin et soir est égale à 0,385.
3. Démontrer que la probabilité de l'événement S est égale à 0,493.
Formule des probabilité totale.
p(S) = 0,385 +0,108 = 0,493
4. On sait que Louise a ramené Zoé le soir. Quelle est la probabilité qu'elle ait emmenée le matin ?
PS(M) =P(S n M) / P(S) =0,385 / 0,493 =0,781.
Partie B..
Le
temps de trajet de Louise, en minute, entre son domicile et son
travail, peut être modélisé par une variable aléatoire X qui suit la
loi normale d'espérance 28 et d'écart-type 5.
1. Calculer P(X < 25).
P(X < 25) = 0,274.
2. Calculer la probabilité que le temps du trajet soit compris entre 18 et 38 minutes.
P(X < 38) = 0,977 ; P(X < 18) = 0,023 ; P(18 < X < 38) = 0,977 -0,023 =0,954.
3. Déterminer la durée du trajet, arrondie à la minute, telle que P(X > d)=0,1.
P(X < d) = 0,9. La calculatrice donne d ~ 34
4.
Louise a maintenant trouvé un itinéraire plus rapide. Le temps du
trajet peut être modélisé par une variable aléatoire Y qui suit la loi
normale d'espérance 26 et d'écart-type s. On sait que P(Y > 30) =0,1. Calculer s.
P(Y < 30) =0,9.
s = 3,12.
Partie C.
L'entreprise
de Louise indique que 35 % des salariés pratiquent le covoiturage. Un
sondage effectué au sein de l'entreprise montre que sur 254 salariés
choisis au hasarsd, 82 pratiquent le covoiturage. Ce sondage remet-il
en cause l'information de l'entreprise ?
n = 254 ; p = 0,35 ; [ p(1-p) / n ]½= (0,35 x0,65 / 254)½
=0,02993.
1,96 x[ p(1-p) / n ]½=1,96
x0,02993 ~0,05866.
0,35 -0,05866 ~0,291 ; 0,35 +0,05866 ~0,409.
Intervalle de fluctuation asymptotique à 95 % : [0,291 ; 0,409 ].
Fréquence observée 82 / 254 = 0,323.
La fréquence observée appartient à l'intervalle de fluctuation.
Au risque de 5 %, nn ne peut pas mettre en doute l'affirmation de l'entreprise.
Exercice 2. 6 points.
Partie A.
La fonction g est définie sur [0 ; + oo[ par : g(x) = 1-e-x.
1. déterminer la lilite de cette fonction en plus l'infini.
Quand x tend vers plus l'infini e-x tend vers zéro et la fonction g tend vers 1.
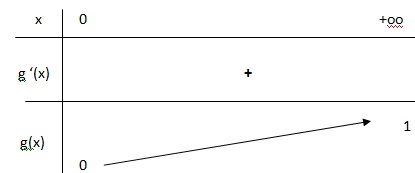
2. Etudier les variations de la fonction g et dresser son tableau de variations.
g'(x)= e-x, positive ; g est strictement croissante sur [0 ; + oo[
Partie B.
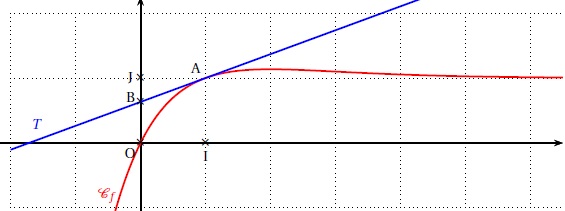
On considère la fonction f définie sur R par f(x) =(x-1)e-kx +1 avec k réel strictement positif.
On a représenté la courbe C pour une certaine valeur de k.
1.a Démontrer que f '(x) = e-kx(-kx+k+1).
On pose u = x-1 et v = e-kx ; u' = 1 ; v' = -ke-kx.
u'v +v'u = e-kx-ke-kx(x-1) =e-kx(-kx+k+1).
b. Démontrer que l'ordonnée du point B est égale à g(k) ou g est la fonction définie dans la partie A.
Coefficient directeur de la tangente à la courbe C en A :
f '(1) =e-k((-k+k+1) = e-k.
Equation de cette tangente : y = e-k x+b.
A (1 ; f(1)=1 ) appartient à la tangente.
1 = e-k +b ; b =1-e-k.
y = e-k x +1-e-k.
B( 0 ; yB) appartient à cette tangente.
yB = 1-e-k= g(k).
2. Démontrer que le point B appartient au segment [OJ].
yJ = 1 ; de plus g(x) est strictement inférieur à1.
yB = g(k) < 1 ; B appartient au segment [OJ].
Partie C.
On considère la fonction h définie sur R par : h(x) = (x-1)e-2x+1.
On note Ch la courbe représentative de la fonction h et d la droite d'équation y = x.
On admet que la droite d est au dessous de Ch sur [0 ; 1 ].
Soit D le domaine du plan délimité par la courbe Ch, la droite d et les droites d'équations x=0 et x = 1. Soit A l'aire de D exprimée en unité d'aire
1. Hachurer le domaine D et démontrer que 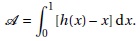
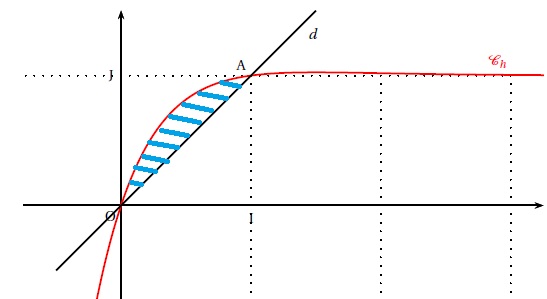
Aire hachurée = aire du domaine comprise entre la courbe Ch, l'axe des abscisses et les droites d'équations x=0 et x=1, diminiuée de l'aire du triangle OAI soit 0,5.
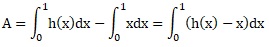
2.a. Démontrer que pour tout x réel, h(x)-x=(1-x)(1-e-2x).
(x-1)e-2x+1-x=(1-x) ( 1-e-2x).
b. On admet que, pour tout réel x, e-2x > 1-2x.
Démontrer que, pour tout réel x de [0 ; 1 ], h(x)-x < 2x-2x2.
-e-2x < 2x -1 ;1 -e-2x < 2x ;
(1-x) ( 1-e-2x) < 2x(1-x) ; (1-x) ( 1-e-2x) < 2x-2x2.
c. En déduire que A < 1 /3.
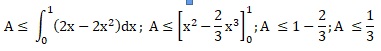
3. Soit H la fonction définie sur [0 ; 1] par H(x) = 0,25(1-2x)e-2x+x.
On admet que H est une primitive de h sur [0 ; 1 ]. Déterminer la valeur exacte de A.
A =H(1)-H(0) -0,5.
H(1)=0,25 (-e-2)+ 1 ; H(0)= 0,25 ;
A = -0,25 e-2+ 1-0,25 - 0,5 = -0,25e-2+0,25.
|
...
|
....
|
Exercice 3. 4 points.
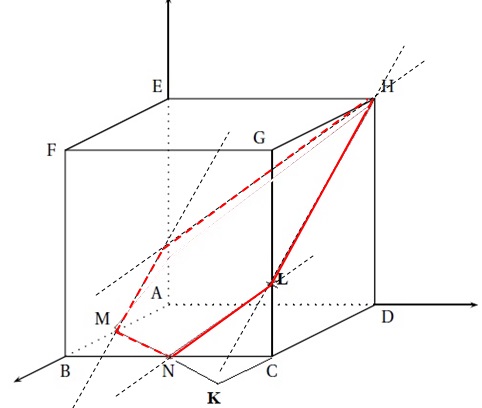
M et N sont les milieux respectifs des segments [AB) et [BC].
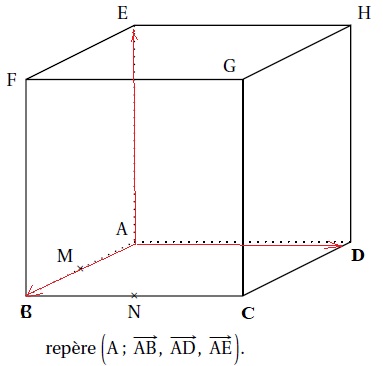
1. Donner sans justifier les coordonnées des points H, M et N.
H(0 ; 1 ; 1 ) ; M(0,5 ; 0 ; 0) ; N( 1 ; 0,5 ; 0).
2. On admet que les droites (CD) et (MN) sont sécantes et on note K leur point d'intersection.
a. Donner une représentation paramétrique de la droite (MN).
Coordonnées du vecteur MN : 0,5 ; 0,5 ; 0.
Représentation paramétrique de la droite (MN) :
x = 0,5 t'+xM =0,5 t' +0,5 ; y = 0,5 t' +yM = 0,5 t' ; z = 0 t'+zM = 0 avec t ' réel.
On admet qu'une représentation paramétrique de la droite (CD) est :x = t ; y = 1 ; z = 0 avec t réel.
b. Déterminer les coordonnées du point K.
yK =0,5 t' =1 soit t' = 2.
xK = 0,5 t' + 0,5 = t soit t=1,5.
zK = 0.
Coordonnées du point K : 1,5 ; 1 ; 0.
3. On admet que les
points H, M et N définissent un plan et que la droite (CG) et le plan
(HMN) sont sécants. On note L leur point d'intersection.
a. Vérifier que le vecteur de coordonnées(2 ; -2 ; 3) est un vecteur normal au plan (HMN).

b. Déterminer une équation cartésienne du plan (HMN).
2x-2y+3z+d=0.
M appartient à ce plan : 2 *0,5 +0 +0 +d = 0 ; d = -1.
2x-2y+3z-1=0.
c. En déduire les coordonnées du point L.
Représentation paramétrique de la droite (CG) :
x = xC =1 ; y = yC=1 ; z = t+zC = t avec t réel.
L appartient à cette droite : xL = 1 ; yL = 1 ; zL = t.
L appartient au plan (HMN) :
2xL-2yL+3zL-1=0.
2-2+3t-1=0 t = 1,/3.
L ( 1 ; 1 ; 1 /3).
4. Construire les points K,et L puis l'intersection du cube par le plan (HMN).
Exercice 4. QCM. 5 points.
1. Soit (un) la suite définie par : u0 = 4 et un+1 = -2 /3 un +1 pour tout entier n.
Soit (vn) la suite définie par vn = un -2 /3.
Affirmation 1 : la suite (vn) est géométrique. Faux.
vn+1 = un+1 -2 /3 = -2 /3 un +1-2 / 3 = -2 /3 un +1 / 3 = -2 / 3 (un-0,5)
vn+1 différe de k vn avec k réel, la suite (vn) n'est pas géométrique.
2. Soit (wn) définie par wn = [3 +cos(n)] / n2 pour tout entier naturel non nul.
Affirmation 2 : cette suite converge vers zéro. Vrai.
cos(n) est compris entre -1 et +1.
Le numérateur appartient à l'intervalle [2 ; 4].
Quand n tend vers l'infini, wn tend vers zéro.
3. On considère l'algorithme suivant :
U=5
N=0
Tant que U < 5000
U = 3 *U-8
N=N+1
Fin Tant que
Affirmation 3 : à la fin de l'excécution, la variable U contient la valeur 5000. Faux.
N
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
U
|
5
|
7
|
13
|
31
|
85
|
247
|
733
|
2191
|
6565
|
U < 5000
|
vrai
|
vrai |
vrai |
vrai |
vrai |
vrai |
vrai |
vrai |
faux
|
4. On considère
l'équation (E) d'inconnue z dans l'ensemble des nombres complexes.
(z-i)(z2+3½z+1)=0.
Affirmation 4 : toutes les solutions de l'équation (E) sont de module 1. Vrai.
z-i = 0 ; solution z = i ; le module de z est égal à 1.
z2+3½z+1=0 ; discriminant D = 3-4=-1=i2.
Solutions z1 =(-3½ +i) / 2 et z2 =(-3½ -i) / 2.
Module de z1 = module de z2 = [(3+1)/4]½ =1.
5. On considère les nombres complexes zn définis par :
z0 = 2 et pour tout entier naturel n, zn+1 = 2 exp(ip/2) zn.
On note Mn le point d'affixe zn.
Affirmation 5 : pour tout entier naturel n, le point O est le milieu du segment [MnMn+2]. Faux.
z1 = 2 exp(ip/2) z0 =4 exp(ip/2)= 4 i.
z2 = 2 exp(ip/2) z1 =8 exp(ip/2) exp(ip/2) = 8 exp(ip) = -8.
Le milieu du segment M0M2 a pour abscisse (2+(-8)) / 2 = -3.
|
|