Math�matiques, suite, g�om�trie, probabilit�s, bac Asie 2021. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicit�s adapt�es � vos centres d’int�r�ts. .. .. . . .. .. ...... ... Suites. En 2020, une influenceuse sur les r�seaux sociaux compte 1 000 abonn�s � son profil. On mod�lise le nombre d’abonn�s ainsi : chaque ann�e, elle perd 10% de ses abonn�s auxquels s’ajoutent 250 nouveaux abonn�s. Pour tout entier naturel n, on note un le nombre d’abonn�s � son profil en l’ann�e (2020+n), suivant cette mod�lisation. Ainsi u0 =1000. 1. Calculer u1. u1=0,90 u0+250 = 0,9 x1000 +250 =1150. 2. Justifier que pour tout entier naturel n, un+1 = 0,9un +250. Chaque ann�e, elle perd 10% de ses abonn�s soit 0,9 x un ; auxquels s’ajoutent 250 nouveaux abonn�s soit 0,9un +250. 3. La fonction Python nomm�e � suite � est d�finie ci-dessous. Dans le contexte de l’exercice, interpr�ter la valeur renvoy�e par suite(10). def suite( n) : u = 1 000 for i in range(n) : u = 0,9*u + 250 return u. Il s'agit du nombre d'abonn�s en l'an 2020+10 = 2030. 4. a. Montrer, � l’aide d’un raisonnement par r�currence, que pour tout entier naturel n, un < 2500. Initialisation : u0 = 1000 < 2500, la propri�t� est vraie au rang z�ro. H�r�dit� : la propri�t� est vraie au rang n. un < 2500. D�montrons qu'elle est vraie au rang n+1 : 0,9 un < 0,9 x2500 ; 0,9 un < 2250 ; 0,9 un +250 < 2250 +250 ; 0,9 un +250 < 2500 ; un+1 < 2500. Conclusion : la propri�t� est vraie au rang z�ro et h�r�ditaire, elle est donc vraie pour tout entier n. b. D�montrer que la suite (un) est croissante. un+1-un = 0,9un +250- un = -0,1 un +250. -0,1 un +250 > -0,1 x2500 +250 =0. un+1-un > 0 ; un+1 > un . La suite est croissante. c. D�duire des questions pr�c�dentes que la suite (un) est convergente. La suite est croissante et born�e, donc elle converge. 5. Soit (vn) la suite d�finie par vn = un −2500 pour tout entier naturel n. a. Montrer que la suite (vn) est une suite g�om�trique de raison 0,9 et de terme initial v0 = −1500. vn+1 = un+1 −2500 =0,9un +250 -2500 = 0,9(un-2500) = 0,9 vn. v0 =u0-2500 =1000 -2500 = -1500. b. Pour tout entier naturel n, exprimer vn en fonction de n et montrer que : un = −1500�0,9n +2500. vn = v0 x0,9n = -1500 x0,9n. un = vn +2500 =−1500�0,9n +2500. c. D�terminer la limite de la suite (un) et interpr�ter dans le contexte de l’exercice. -1 < 0,9 < 1 ; 0,9n tend vers z�ro quand n tend vers plus l'infini. un tend vers 2500. Au bout d'un grand nombre d'ann�es, le nombre d'abonn�s est �gal � 2500. 6. �crire un programme qui permet de d�terminer en quelle ann�e le nombre d’abonn�s d�passera 2 200. D�terminer cette ann�e. u =1000 n =0 while u < 2200 u = 0,9 *u+250. n = n+1 Fin tant que return n −1500�0,9n +2500 > 2200 ; −1500�0,9n  > -300 ; 1500�0,9n  < 300 ; 0,9n  < 0,2 ; n ln(0,9) < ln(0,2) ; n < ln(0,2) / ln(0,9) ; n > 15,27 soit 16. ( ann�e 2020 +16 = 2036). G�om�trie. On consid�re un cube ABCDEFGH d’ar�te 8 cm et de centre �W. 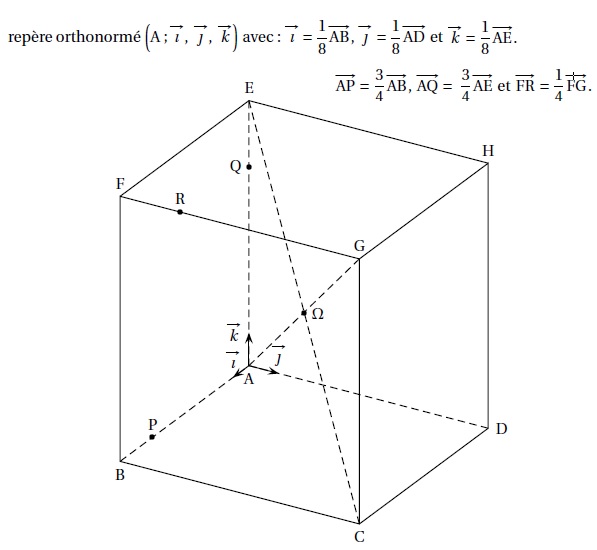Partie I. 1. Dans ce rep�re, on admet que les coordonn�es du point R sont (8; 2; 8). Donner les coordonn�es des points P et Q. 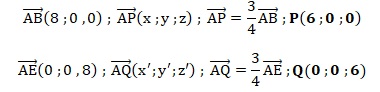2. Montrer que le vecteur n de coordonn�es (1 ; −5 ; 1) est un vecteur normal au plan (PQR). 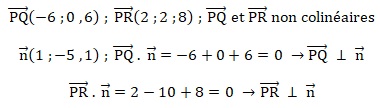3. Justifier qu’une �quation cart�sienne du plan (PQR) est x −5y +z −6 =0. Le vecteur n de coordonn�es (1 ; −5 ; 1) est un vecteur normal au plan (PQR). Equation cart�sienne de ce plan : x-5y+z+d=0. P(6 ; 0 ; 0) appartient � ce plan : 6+d = 0 doit d = -6. Equation cart�sienne du plan (PQR) est x −5y +z −6 =0. Partie II. On note L le projet� orthogonal du point � W sur le plan (PQR). 1. Justifier que les coordonn�es du point � W sont (4; 4; 4). W est le centre du cube de c�t� 8 cm et le sommet A est l'origine du rep�re. 2. Donner une repr�sentation param�trique de la droite d perpendiculaire au plan (PQR) et passant par �W. Le vecteur n de coordonn�es (1 ; −5 ; 1) est un vecteur directeur de la droite (d) et le centre du cube appartient � cette droite. Equation param�trique de cette droite : x = t +xW ; y = -5t +yW ; z = t +zW avec t r�el. x = t+4 ; y = -5t+4 ; z = t+4. 3. Montrer que les coordonn�es du point L sont ( 14 / 3 ; 2 / 3 ; 14 / 3). 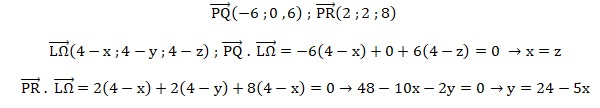L appartient au plan (PQR) d'�quation cart�sienne x −5y +z −6 =0. x-5(24-5x)+x-6 = 0 soit x =  126 / 27= 14 /3. y = 24-5 *14/3 =24-70 / 3 = (72-70) / 3 = 2 /3. 4. Calculer la distance du point � W au plan (PQR). LW2 =(4-14 / 3)2 +(4-2 / 3)2 +(4-14 / 3)2 )=(-2 / 3)2 +(10 / 3)2 +(-2 / 3)2 )=108  / 9 = 12. LW =2 *3�. ... .... Probabilit�s. Un sac contient les huit lettres suivantes : A B C D E F G H (2 voyelles et 6 consonnes). Un jeu consiste � tirer simultan�ment au hasard deux lettres dans ce sac. On gagne si le tirage est constitu� d’une voyelle et d’une consonne. 1. Un joueur extrait simultan�ment deux lettres du sac. a. D�terminer le nombre de tirages possibles. C82 =8 x 7 / 2 = 28. b. D�terminer la probabilit� que le joueur gagne � ce jeu. AB ; AC ; AD ; AE ; AF ; AG ; AH ; BC ; BD ; BE ; BF ; BG ; BH ; CD : CE ; CF ; CG ; CH ; DE ; DF ; DG ; DH ; EF ; EG ; EH ; FG ; FH ; GH. 12 possibilit�s de gain sur 28 cas possibles. 12 / 28 = 3 / 7. Les questions 2 et 3 de cet exercice sont ind�pendantes. Pour la suite de l’exercice, on admet que la probabilit� que le joueur gagne est �gale � 3 / 7. 2. Pour jouer, le joueur doit payer k euros, k d�signant un entier naturel non nul. Si le joueur gagne, il remporte la somme de 10 euros, sinon il ne remporte rien. On note G la variable al�atoire �gale au gain alg�brique d’un joueur (c’est-�-dire la somme remport�e � laquelle on soustrait la somme pay�e). a. D�terminer la loi de probabilit� de G. G 10-k (on gagne) -k ( on perd) probabilit� 3 / 7 4/7 b. Quelle doit �tre la valeur maximale de la somme pay�e au d�part pour que le jeu reste favorable au joueur ? La moyenne des gain doit �tre positive : (10-k) 3 /7 -4k / 7 > 0. (10-k) x3 -4k >0. 30-3k-4k >0 30 > 7 k ; k < 30 / 7 soit environ 4,29 €. 3. Dix joueurs font chacun une partie. Les lettres tir�es sont remises dans le sac apr�s chaque partie. On note X la variable al�atoire �gale au nombre de joueurs gagnants. a. Justifier que X suit une loi binomiale et donner ses param�tres. Chaque tirage est ind�pendant des autres tirages et deux issues sont possibles : on gagne ou on perd. X suit la loi binomiale de param�tres n = 10 et p = 3 / 7. b. Calculer la probabilit�, arrondie � 10−3, qu’il y ait exactement quatre joueurs gagnants. P(X = 4) = 0,247. c. Calculer P(X >5) en arrondissant � 10−3. Donner une interpr�tation du r�sultat obtenu. P(X >5) = 1-P(X < 5) = 1-0,782 =0,218. La probabilit� que plus de la moiti� des joueurs gagne est �gale � 0,218. d. D�terminer le plus petit entier naturel n tel que P(X < n) >0,9. P(X < 6) =0,92 ; P(X < 5) =0,78 ; n = 6..

menu