Math�matiques,
logarithme, exponentielle, bac Asie 2021.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicit�s adapt�es � vos centres
d’int�r�ts.
..
..
|
.
.
|
..
..
......
...
|
Logarithme.
Partie I : lectures
graphiques.
f d�signe une fonction d�finie et d�rivable sur R.
On donne ci-dessous la courbe repr�sentative de la fonction d�riv�e f ′.
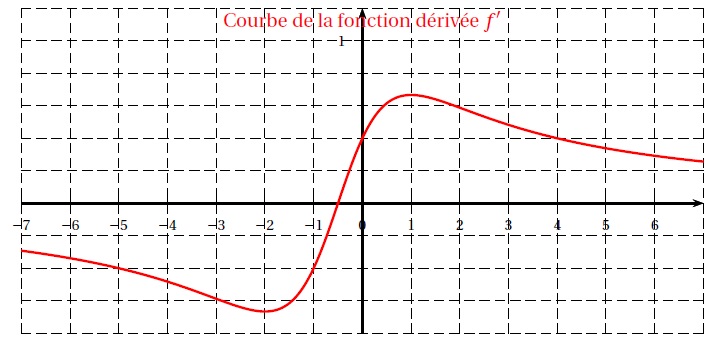
Avec la pr�cision permise par le graphique, r�pondre aux questions
suivantes
1. D�terminer le
coefficient directeur de la tangente � la courbe de la fonction f en O.
f '(0) = 0,4.
2. a. Donner les
variations de la fonction d�riv�e f ′.
f '(-2) = 0 ; f '(1) = 0.
b. En d�duire un
intervalle sur lequel f est convexe.
La d�riv�e f '(x) est croissante sur [-2 ; 1] ; f(x) est convexe sur
cet intervalle.
Partie II : �tude de
fonction.
La fonction f est d�finie sur R par
f (x) = ln(x2 +x +2,5)�.
1. Calculer les
limites de la fonction f en +∞et en −∞.
Quand x tend vers plus l'infini : x2 +x
+2,5 tend vers plus l'infini et f(x) tend vers plus l'infini.
Quand x tend vers moins l'infini : x2 +x
+2,5 tend vers plus l'infini et f(x) tend vers plus l'infini.
2.
D�terminer une expression f ′(x) de la fonction d�riv�e de f pour tout
x ∈ R.
On pose u =x2+x+2,5 ; u' = 2x+1.
f '(x) = u ' / u = (2x+1) / (x2+x+2,5).
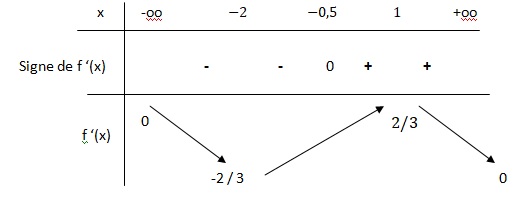
3. En d�duire le
tableau des variations de f . On veillera � placer les limites dans ce
tableau.
x2+x+2,5
>0 ; f '(x) a le signe de 2x+1.
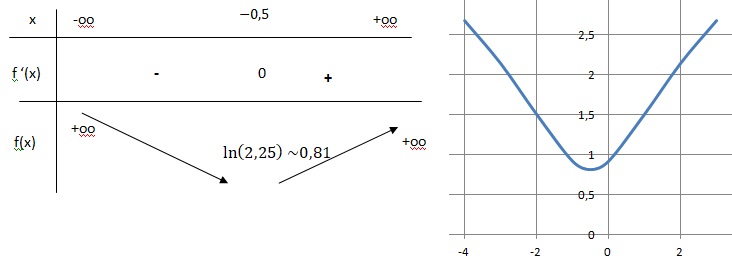
4. a. Justifier que l’�quation f (x) =2 a une unique solution a dans l’intervalle [−0,5 ;
+∞[.
Sur l’intervalle
[−0,5 ; +∞], f(x) est strictement croissante.
f(-0,5) =ln(2,25) < 2 et f(x) tend vers plus l'infini si x tend vers
plus l'infini.
D'apr�s le th�or�me de la bijection, f (x) =2 a une
unique solution a
dans l’intervalle [−0,5 ; +∞[.
b.
Donner une valeur approch�e de a
� 10−1 pr�s.
a ~1,8.
5. La fonction f ′
est d�rivable sur R. On admet que, pour tout x ∈ R, f ′′(x) =(−2x2
−2x +4) / (x2+x +2,5)
D�terminer le nombre de points d’inflexion de la courbe repr�sentative
de f .
Solutions de −2x2 −2x +4 =0 :
Discriminant D =
(-2)2 -4(-2)*4 =36 = 62.
Solutions : x1 = (2-6) / (-4) =1 et x2 = (2+6) / (-4) = -2.
La d�riv�e seconde s'annule et change de signe pour x = -2 et x = 1. La
courbe pr�sente deux points d'inflexion.
|
...
|
....
|
Exponentielle.
Partie 1.
Consid�rons l’�quation diff�rentielle
y′ = −0,4y +0,4 (E)
o� y d�signe une fonction de la variable t , d�finie et d�rivable sur
[0 ; +∞[.
1. a. D�terminer
une solution particuli�re constante de cette �quation diff�rentielle.
y' = 0 soit -0,4y +0,4 = 0 soit y = 1.
b. En d�duire
l’ensemble des solutions de cette �quation diff�rentielle.
Solution g�n�rale de y' +0,4 y =0 :
y = A e-0,4 t avec A une constante.
Solution g�n�rale de (E) :
y = A e-0,4 t +1.
c. D�terminer la fonction g,
solution de cette �quation diff�rentielle, qui v�rifie g(0) = 10.
10 = A e0+1 ; A = 9.
g(t) = 9 e-0,4 t +1.
Partie II.
Soit p la fonction d�finie et d�rivable sur l’intervalle [0 ; +∞[ par
p(t )= 1 /g(t ) =1 / (1+9e−0,4t).
1. D�terminer la
limite de p en plus l'infini.
e−0,4t tend vers
z�ro si t tend vers plus l'infini et p(t) tend vers1.
2. Montrer que p′(t )=3,6e−0,4t
/ ( 1+9e−0,4t )2 pour tout t ∈ [0 ; +∞[.
On pose u = 1+9e−0,4t ; u' =
-9 *0,4 e−0,4t ;
p'(t) = -u'(t) u-2 =3,6e−0,4t / (
1+9e−0,4t )2 .
3. a. Montrer que l’�quation p(t
)=0,5 admet une unique solution a
sur [0 ; +∞[.
p'(t) est strictement positive sur [0 ; +∞[.
p(t) est strictement croissante sur cet intervalle.
p(0) =0,10 < 0,5 ; si t tend vers plus l'infini
et p(t) tend vers1.
D'apr�s le th�or�me
de la bijection, p (t) =0,5 a une unique solution a dans l’intervalle [0 ; +∞[.
b. D�terminer une valeur approch�e
de a � 10−1
pr�s � l’aide d’une calculatrice.
a =
5,5.
Partie III
1. p d�signe la
fonction de la partie II.
V�rifier que p est solution de l’�quation diff�rentielle y′=0,4y(1−y)
avec la condition initiale y(0) =0,1 o� y d�signe une fonction d�finie
et d�rivable sur [0 ; +∞[.
p(t )= 1 / (1+9e−0,4t).
p′(t )=3,6e−0,4t /
( 1+9e−0,4t )2 .
Repport dans l'�quation diff�rentielle :
3,6e−0,4t / (
1+9e−0,4t )2 =0,4[1-1 /
(1+9e−0,4t)] / (1+9e−0,4t).
3,6e−0,4t / (
1+9e−0,4t )2 =0,4[9e−0,4t] /
(1+9e−0,4t)2 est v�rifi�e quel que soit t.
2. Dans un pays en voie de
d�veloppement, en l’ann�e 2020, 10% des �coles ont acc�s � internet.
Une politique volontariste d’�quipement est mise en oeuvre et on
s’int�resse � l’�volution de la proportion des �coles ayant acc�s �
internet.
On note t le temps �coul�, exprim� en ann�e, depuis l’ann�e 2020.
La proportion des �coles ayant acc�s � internet � l’instant t est
mod�lis�e par p(t ).
Interpr�ter dans ce contexte la limite de la question II 1 puis la
valeur approch�e de a
de la question II 3. b. ainsi que la valeur p(0).
p(0) = 0,1 : en 2020 10 % des �coles ont acc�s � internet.
Au cours des ann�es 2025 - 2026 la moiti� des �coles auront acc�s �
internet.
Au bout d'un temps tr�s
long, toutes les �coles auront acc�s � internet.
|
|
