Mathématiques, QCM, géométrie, probabilités, bac Asie 2021. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. .. .. . . .. .. ...... ... QCM. Pas de justification, une seule proposition exacte. 1. On considère la fonction f définie sur R par f (x) = (x2 −2x −1)ex . A. La fonction dérivée de f est la fonction définie par f œ'(x) = (2x −2)ex . Faux. u = x2-2x-1 ; v = ex ; u' = 2x-2 ; v' = ex. u'v+v'u = (2x-2)ex+‰(x2 −2x −1Ž)ex =‰(x2 −3Ž)ex . B. La fonction f est décroissante sur l’intervalle ]−∞; 2]. Faux. f '(x)  > sur ]-oo ; -3½] ; f(x) est croissante sur cet intervalle ]-oo ; -3½] . 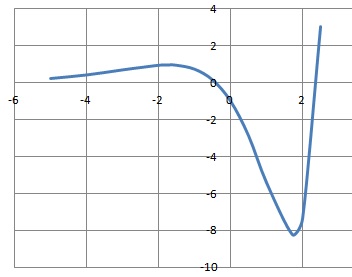C. f(x) tend vers zéro si x tend vers moins l'infini. Vrai. ex tend vers zéro si x tend vers moins l'infini. 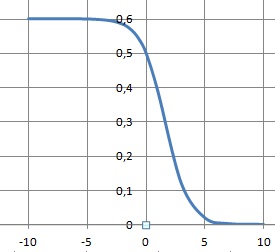2. On considère la fonction f définie sur R par f (x) =3 / (5+ex). Sa courbe représentative dans un repère admet : A. une seule asymptote horizontale ; faux. Quand x tend vers moins l'infini ex tend vers zéro et f(x) tend vers 3 /5. La droite d'équation y = 3 / 5 est asymptote à la courbe. Quand x tend vers plus l'infini ex tend vers plus l'infini et f(x) tend vers zéro. La droite d'équation y = 0 est asymptote à la courbe. B. une asymptote horizontale et une asymptote verticale ; faux. C. deux asymptotes horizontales. Vrai. 3. On donne ci-dessous la courbe Cf œœ représentant la fonction dérivée seconde f œœ d’une fonction f définie et deux fois dérivable sur l’intervalle [−3,5 ; 6]. 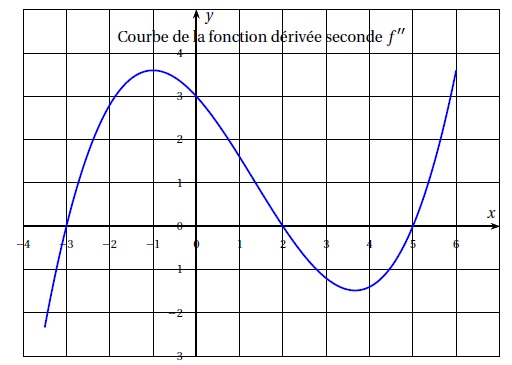A. La fonction f est convexe sur l’intervalle [−3 ; 3]. Faux. La dérivée seconde est positive sur [-3 ; 2] et sur [5 ; +oo[. La fonction est convexe sur ces deux intervalles. B. La fonction f admet trois points d’inflexion. Vrai. La dérivée seconde s'annule et change de signe pour x = -3 ; 2 ; 5. C. La fonction dérivée f ' de f est décroissante sur l’intervalle [0; 2]. Faux. Sur l’intervalle [0; 2], f " est posive et f ' est croissante. 4. On considère la suite (un) définie pour tout entier naturel n par un = n2 −17n +20. A. La suite (un) est minorée. Vrai. 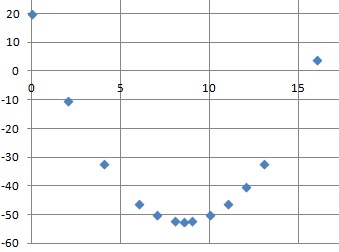B. La suite (un) est décroissante. Faux. C. L’un des termes de la suite (un) est égal à 2 021. Faux. n2 −17n +20 = 2021. n2-17n-2001=0. Discriminant D = (-17)2 +4*2001=8293. Pas de solutions appartenant à N. 5. On considère la suite (un) définie par u0 = 2 et, pour tout entier naturel n, un+1 = 0,75un +5. On considère la fonction « seuil » suivante écrite en Python : def seuil : u = 2 n = 0 while u < 45 : u = 0,75*u + 5 n = n+1 return n Cette fonction renvoie : A. la plus petite valeur de n telle que un ⩾ 45 ; vrai. B. la plus petite valeur de n telle que un < 45 ; C. la plus grande valeur de n telle que un ⩾ 45. Géométrie. On considère un pavé droit ABCDEFGH tel que AB = AD = 1 et AE = 2, représenté ci- dessous. Le point I est le milieu du segment [AE]. Le point K est le milieu du segment [DC].  N est le projeté orthogonal du point D sur le plan (AKL). 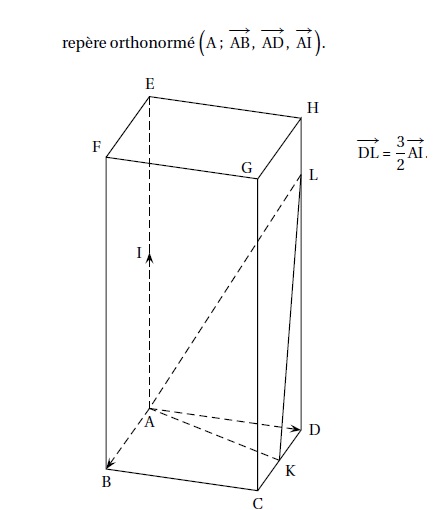On admet que le point L a pour coordonnées (0 ; 1 ; 1,5). 1. Déterminer les coordonnées des vecteurs suivants. K( 0,5 ; 1 ; 0) ; I ( 0 ; 0 ; 1). 2. a. Démontrer que le vecteur n de coordonnées (6 ; −3 ; 2) est un vecteur normal au plan (AKL). b. En déduire une équation cartésienne du plan (AKL). 6x-3y+2z +d = 0. A (0 : 0 : 0) appartient à ce plan, donc d = 0. 6x-3y+2z = 0. c. Déterminer un système d’équations paramétriques de la droite D passant par D et perpendiculaire au plan (AKL). Le vecteur n (6 ; -3 ; 2) est un vecteur directeur de la droite D et D(0 ; 1 ; 0 ) appartient à cette droite. x =6t+xD ; y = -3t +yD ; z = 2t+zD avec t réel. x =6t ; y = -3t +1 ; z = 2t. d. En déduire que le point N de coordonnées (18 /49 ; 40 / 49 : 6 / 49 )  est le projeté orthogonal du point D sur le plan (AKL). N(x ; y ; z ) appartient au plan (AKL) : 6x-3y+2z = 0. N appartient à la droite D : x =6t ; y = -3t +1 ; z = 2t. 36t-3(-3t+1)+4t=0 49 t = 3 ; t = 3 / 49. Par suite x = 18 / 49 ; y = -9 / 49 +1 = (-9+49) / 49 = 40 / 49 ; z = 6 / 49. 3. a. Calculer le volume du tétraèdre ADKL en utilisant le triangle ADK comme base. Aire du triangle AKD : AD x DK / 2 = 1 x0,5 /2 = 0,25 unité d'aire. Hauteur DL = 1,5. Volume du tétraèdre ADKL : aire du triangle AKD  x DL / 3 = 0,25 x1,5 / 3 =0,125 unités de volume. b. Calculer la distance du point D au plan (AKL). DN2 = (18 / 49)2 +(40 / 49 -1)2 +(6 / 49)2 = (182 +(-9)2 +62) / 492 =(21 / 49)2. DN = 21 / 49 = 3 / 7. c. Déduire des questions précédentes l’aire du triangle AKL. Volume du tétraèdre ADKL = aire du triangle AKL x DN / 3. Aire du triangle AKL = 3 x 0,125 x 7 / 3 = 0,875 unité d'aire. ... .... Probabilités. Une société de jeu en ligne propose une nouvelle application pour smartphone nommée « Tickets coeurs! ». Chaque participant génère sur son smartphone un ticket comportant une grille de taille 3×3 sur laquelle sont placés trois coeurs répartis au hasard, comme par exemple ci-dessous. 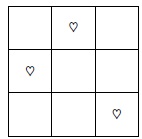Le ticket est gagnant si les trois coeurs sont positionnés côte à côte sur une même ligne, sur une même colonne ou sur une même diagonale. 1. Justifier qu’il y a exactement 84 façons différentes de positionner les trois coeurs sur une grille. C93 = 9 x 8 x7 / (3 x2) =84. 2. Montrer que la probabilité qu’un ticket soit gagnant est égale à 2 / 21. Nombre de cas favorables : 3 lignes + 3 colonnes + 2 diagonales soit 8. Probabilité d'un ticket gagnant : 8 / 84 = 2 / 21. 3. Lorsqu’un joueur génère un ticket, la société prélève 1  € sur son compte en banque. Si le ticket est gagnant, la société verse alors au joueur 5 €. Le jeu est-il favorable au joueur ? On note G la variable aléatoire égale au gain algébrique d’un joueur (c’est-à-dire la somme remportée à laquelle on soustrait la somme payée). Loi de probabilité de G. G 5-1 = 4 (on gagne) -1 ( on perd) probabilité 2 / 21 19 / 21 Moyenne : 8 / 21 -19 / 21 = -11 / 21. Le jeu est défavorable au joueur. 4. Un joueur décide de générer 20 tickets sur cette application. On suppose que les générations des tickets sont indépendantes entre elles. a. Donner la loi de probabilité de la variable aléatoire X qui compte le nombre de tickets gagnants parmi les 20 tickets générés. Chaque génération de ticket est indépendant des autresgénérations et deux issues sont possibles : on gagne ou on perd. X suit la loi binomiale de paramètres n = 20 et p = 2 / 21. b. Calculer la probabilité, arrondie à 10−3, de l’évènement (X = 5). P(X = 5) = 0,0270. c. Calculer la probabilité, arrondie à 10−3, de l’évènement (X ⩾ 1) et interpréter le résultat dans le contexte de l’exercice. P(X > 1) = 1-P(X=0) = 1-0,1251 = 0,865. Sur 20 tickets, la probabilité de gagner au moins une fois est 0,865.

menu