Mathématiques,
Brevet Amérique du Nord 2020.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
..
..
|
.
.
|
..
..
......
...
|
Exercice
1. 20 points
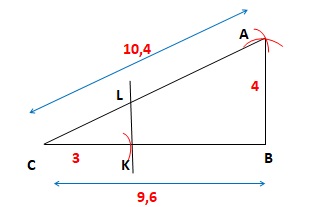
ABC est un triangle tel que : AC = 10,4
cm, AB =4cm et BC = 9,6 cm.
Les points ALet C sont alignés.
Les points B, K et C sont alignés.
La droite (KL) est parallèle à la droite (AB). CK = 3 cm.
1. Construire la
figure en laissant les traits de construction.
2. Prouver que le
triangle ABC est rectangle en B.
AC2 =10,42 =108,16.
AB2 + BC2 =42 +9,62 =108,16.
D'après la réciproque du théorème de Pythagore, le triangle aBC est
rectangle en B.
3. Calculer la
longueur CL en cm.
AB et CL sont parallèles ; A, L, C sont alignés et B, K, C sont alignés.
Relation de Thalès : BC / CK = AC / CL ;
9,6 / 3 = 10,4 / CL ; CL = 10,4 *3 / 9,6 =3,25 cm.
4. Calculer une
valeur approchée de l'angle CAB au degré près.
sin (CAB) = BC / AC =9,6 / 10,4 ~0,923.
L'angle CAB mesure environ 67°.
Exercice 2. QCM. 15
points.
1. Si on multiplie
la longueur de chaque arête d'un cube par 3, alors le volume du cube
sera multiplié par :
3 ; 9 ; 12 ; 27.
Volume du cube = côté 3.
En multipliant par 3 le coté, le volume est multiplié par 33
= 27.
2. Lorsque x = -4, x2+3x+4
est égal à : 8 ; 0 ; -24 ; -13.
(-4)2 +3*(-4)+4 = 16-12+4=8.
3. 1 / 3 +1 /4 est
égal à :2 /7 ; 0,583 ; 7 /12 ;
1 /7.
4 / 12 +3 /12 = (3+4) / 12 = 7 /12.
4. La notation
scientifique de 1 500 000 000 est :
15 10-8 ; 15 108 ; 1,5 10-9 ; 1,5 109.
1 500 000 000 = 1,5 * 1 00 000 000 = 1,5
109.
5. (x-2)*(x+2) est
égal à : x2-4
; x2+4 ; 2x-4 ; 2x.
(x-2)*(x+2) = x2-22 = x2-4.
Exercice 3. 18
points.
1. On considère un carré ABCD de
centre O, partagé en 4 polygones superposables numérotés 1, 2, 3 et 4.
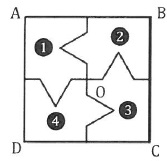
a. Quelle est
l'image du polygone 1 par la symétrie de centre O ?
Le polygone 3.
2. Quelle est
l'image du polygone 4 par la rotation de centre O qui transforme le
polygone 1 en polygone 2.
Rotation de centre O, de 270° ( 3 / 4 de tour) dans le sens contraire
des aiguilles d'une montre.
Ou rotation de centre O, de 90 ° ( 1 / 4 tour), dans le sens des
aiguilles d'une montre.
Dans cette rotation l'image du polygone 4 et le polygone 1.
3. La figure
ci-dessous est un pavage dont le motif de base est le carré ABCD.
Quelle transformation partant du polygone 1 permet d'obtenir le
polygone 5 ?
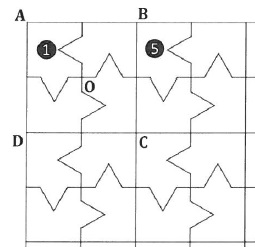
Translation, vers la droite, de longueur AB.
3. On souhaite
faire imprimer ces motifs sur un tissu rectangulaire de longueur 315 cm
et de largeur 270 cm. Le tissu doit être entièrement recouvert de
carrés ABCD, sans découpe et de sorte que le côté du carré mesure un
nombre entier de cm.
a. Montrer qu'on
peut choisir des carrés de 9 cm de côté.
315 / 9 =35 ; 270 / 9 =30.
b. Dans ce cas,
combien de carré seront imprimés sur le tissu ?
Aire du tissu : 315 x 270 =85050 cm2.
Aire d'un carré : 81 cm2.
Nombre de carré : 85 050 /81 =1050.
Ou plus simplement : 30 x35 = 1050.
|
| .
. |
....
|
Exercice 4.
(24 points)
Voici
la série des temps exprimés en secondes, et réalisés par
les nageuses de la finale du 100 m féminin nage libre lors des
championnats d'Europe de natation 2018.
53,23 ; 54,04 ; 53,61 ; 54,52 ; 53,35 ; 52,93 ; 54,56 ; 54,07.
1. La française C.
BONNET est arrivée troisième à cette finale. Quel est le temps de cette
nageuse ?
52,93 ; 53,23 ; 53,35 ; 53,61
; 54,04 ; 54,07 ; 54,52 ; 54,56.
2. Quelle est la
vitesse moyenne de la nageuse ayant parcouru le 100 m en 52,93 s ?
100 / 52,93 ~1,9 m /s.
3. Comparer moyenne
et médiane de cette série.
Moyenne = (52,93+
53,23 + 53,35 + 53,61 + 54,04 + 54,07 + 54,52 + 54,56) / 8 ~53,79.
La médiane est comprise entre 53,61 et 54,04.
Moyenne et médiane peuvent être identiques.
Sur une feuille de calcul, on a reporté le classement des dix premiers
pays selon le nombre de médailles d'or toutes disciplines confondues.
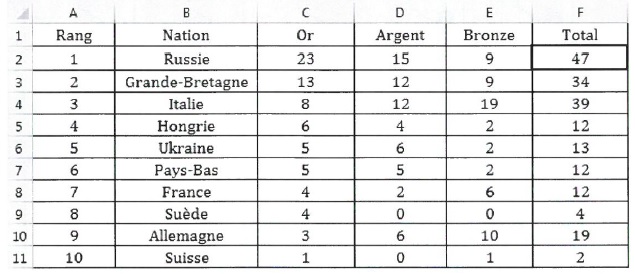
4. Est-il vrai qu'à
elles deux, Grande Bretagne et Italie ont obtenu autant de médailles
d'or que la Russie ?
13 +8 =21 ; Russie : 23 > 21. C'est donc faux.
5. Est-il vrai que
plus de 35 % des médailles remportées par la France sont des médailles
d'or ?
4 médailles d'or sur un total de 12 : 4 / 12 = 1 /3 = 0,33 (33
%). Donc, c'est faux.
6. Quelle formule a
t-on pu saisir dans la cellule F2, avant qu'elle ne soit étirée vers le
bas jusqu'à la cellule F11 ?
= SOMME(C2:E2)
Exercice 5. ( 23
points).
On dispose de deux urnes :
une urne bleue contenant trois boules bleues numérotées 2, 3 et 4 ;
une urne rouge contenant 4 boules rouges numérotées 2, 3, 4 et 5.
Les boules sont indiscernbles au toucher et ont la même probabilité
d'être tirées.
On s'interesse à l'expérience aléatoire suivante :
on tire au hasard une boule bleue et on note son numéro, puis on tire
au hasard une boule rouge et on note son numéro.
On précise que le tirage (3 ; 4) est différent du tirage (4 ; 3).
1. On définit les
événements suivants :
" on obtient deux nombres premiers " et " la somme des deux nombres est
égale à 12".
a. Pour cahcun des événements précédents, dire s'il est possible ou
impossible.
"
on obtient deux nombres premiers " : (2 ; 2) ou (2 ; 3).... c'est
possible.
" a
somme des deux nombres est égale à 12" ; c'est impossible ( 4+5= 9 <
12.
b. Déterminer la
probabilité de l'événement " on obtient deux nombres premiers".
|
2
|
3
|
4
|
5
|
2
|
(2 ; 2) |
(2 ; 3) |
(2 ; 4) |
(2 ; 5) |
3
|
(3 ; 2) |
(3 ; 3)
|
(3 ; 4) |
(3 ; 5) |
4
|
(4 ; 2) |
(4 ; 3) |
(4 ; 4)
|
(4 ; 5) |
6
cas favorables sur 12 cas possibles.
Probabilité cherchée : 6 / 12 =0,5.
2. Justifier que la
probabilité d'obtenir un double ( les deux boules portent le même
numéro) est 0,25.
3 cas favorables sur 12 cas possibles.
Probabilité cherchée : 3 / 12 = 0,25.
3. On souhaite
simuler cette expérience 1000 fois.
On écrit le programme incomplet suivant :
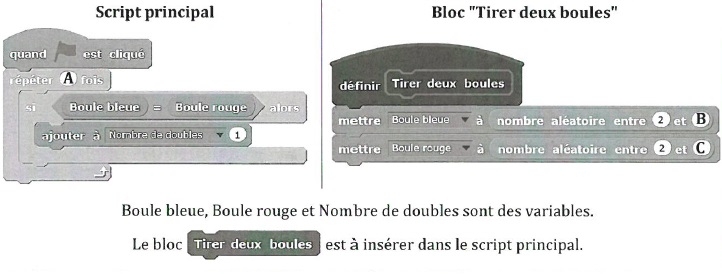
a. Par quels
nombres faut-il remplacer les lettres A, B et C ?
A = 1000 ; B = 4 ; C = 5.
b. Dans le script
principal, indiquer où placer le bloc " Tirer deux boules".
Juste après l'instruction " répéter A fois".
c. Dans le script principal,
indiquer où placer l'élément " mettre Nombre de boules à 0".
Juste
avant l'instruction " répéter A fois".
d. On souhaite obtenir la fréquence d'apparition du nombre de "doubles"
obtenus.
parmi les instructions ci-dessous, laquelle faut-il placer à la fin du
script principal après la boucle "répéter" ?
dire Nombre de doubles ; dire Nombre
de doubles / 1000 vrai
; dire Nombre de doubles / 2.
|
|