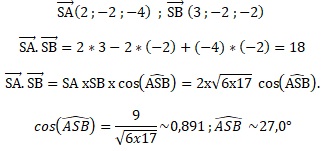Mathématiques, fonctions, suite, géométrie, bac Centres étrangers 2021.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

.. ..


 .
.
.. ..
......


...

Exercice 1, QCM ( 5 points).
Question 1.
Soit la fonction f définie sur R par : f(x) = x e-2x.
Quel que soit le réel x, f ''(x) est égale à :
(1-2x)e-2x ; 4(x-1)e-2x vrai ;  4 e-2x ; (x+2)e-2x.
Calcul de f '(x) en posant u = x ; v = e-2x ; u' = 1 ; v' = -2e-2x.
u'v+v'u = e-2x -2xe-2x = e-2x(1-2x).
Calcul de f ''(x) en posant u = 1-2x ; v = e-2x ; u' = -2 ; v' = -2e-2x.
u'v+v'u = -2e-2x -2(1-2x) e-2x = e-2x(-4+4x) =4(x-1)e-2x.

Question 2.
Un élève choisit trois spécialités parmi  les 12 proposées. Le nombre de combinaisons possibles est :
1728 ; 1320 ; 220 vrai ; 33.
12 x 11 x10  /(1 x2 x3 ) =220.

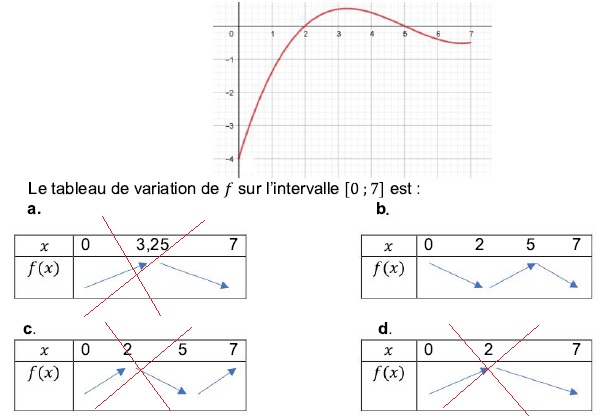
Question 3.
On donne la représentation graphique de f '  fonction dérivée d'une fonction f définie ur [0 ; 7]. Le tableau de variation de f est :


Question 4.
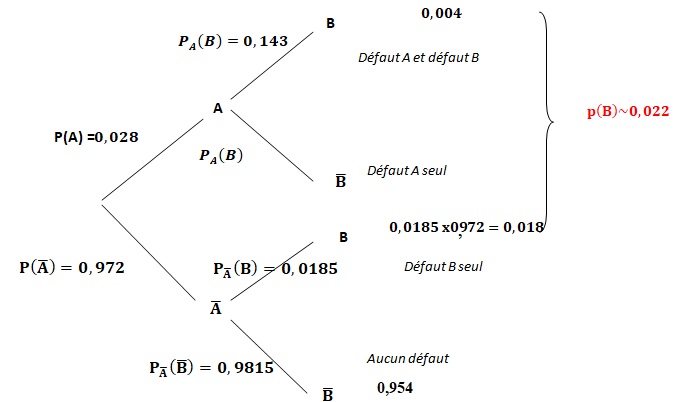
 Une entreprise fabrique des cartes à puces Chaque puce peut présenter deux défauts notés A et B.
2,8 % des puces ont le défaut A, 2,2 % ont le défaut B et 95,4 % des puces n'ont aucun défaut.
La probabilité qu'une puce prélevée au hasard ait les deux  défauts est :
0,05 ; 0,004 vrai ; 0,046 ; on ne peut pas le savoir.


Question 5.
On se donne une fonction f, supposée dérivable sur R et on note f ' sa  dérivée. On donne le tableau de variation de f.

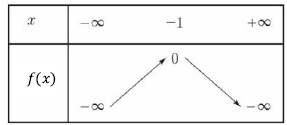
 f ' est positive sur R.
f ' est positive sur ]-oo ; -1]. Vrai ( f est croissante).
f ' est négative sur R.
f ' est positive sur [-1 ; +oo[.

Exercice 2. 5 points.
Les utilisateurs réguliers de  transport en commun représentent 17 % de la population française. Parmi eux, 32 % sont des jeunes âgés de 18 à 24 ans.
Partie A.
On interroge une personne au hasard et on note :
- l'événement R : la personne interrogée utilise régulièrement ces transports ;
- l'événement J : la paersonne est âgée de 18 à 24 ans.
1. Représenter la situation à l'aide d'un  arbre pondéré.

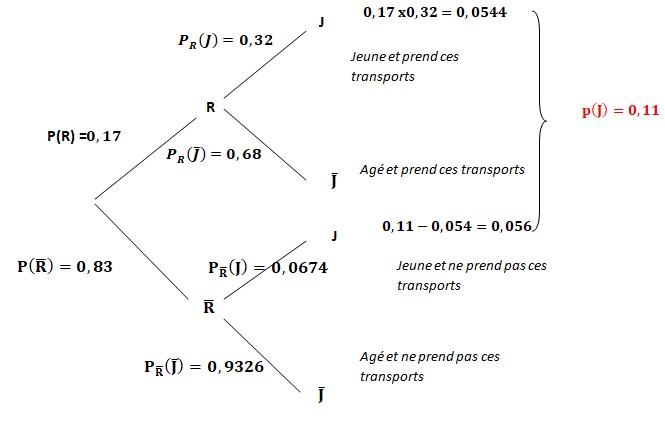2. Calculer P(R n J).
0,17 x0,32 =0,0544.
3. Les jeunes de 18 à 24 ans représentent 11 % de la population française. Montrer que la probabilité que la personne interrogée soit un jeune de 18 à 24 ans n'utilisant pas régulièrement les transports en commun est 0,056.
0,11 -0,054 = 0,056.
4. En déduire la proportion de jeunes de 18 à 24 ans parmi les utilisateurs non réguliers des transports en commun.
Pnon R (J) = p( non R n J) / P(non R) =0,056 / 0,83=0,0674.

Partie B.
Un recenseur interroge au hasard 50 personnes en une journée sur leur pratique des transports en commun. Ce recensement est assimilé à un tirage avec remise.
Soit X la variable aléatoire dénombrant les personnes utilisant régulièrement les transports en commun parmi les 50 personnes interrogées.
1. Déterminer en justifiant la loi de X et préciser ses paramètres.
On choisit 50 personnes de manière indépendante. Deux issues sont possibles " la personne prend ces transports " ou" la personne ne prend pas ces transports".
On répète 50 fois une épreuve de Bernoulli.
X suit une loi binomiale de paramètre n =50 ; p = 0,17.
2. Calculer P(X=5) et interpréter.
P(X=5) =0,0687.
 Parmi 50 personnes interrogées, la probabilité que 5 personnes prennent les transports en commun est 0,0687.
3. Le recenseur indique qu'il y a plus de 95 % de chance pour que parmi les 50 personnes interrogées, moins  de 13 d'entre elles utilisent régulièrement les transports en commun. Cette affirmation est-elle vraie ? Justifier.
P(X < 13) = 0,964.
Cette valeur étant supérieure à 0,95,l'affirmation est vraie.
 4. Quel est le nombre moyen de personnes utilisant régulièrement les transports en commun parmi les 50 personnes interrogées ?
E(X) = n p = 50 x 0,17 =8,5. ( ~ 9 personnes).

...
....

 Exercice 3. (5 points)
Une entreprise de 5000 personnes propose le télétravail. En mai 2020, seuls 200 d'entre eux ont choisi le télétravail. Chaque moins, depuis la mise en place de cette mesure, 85 % des personnes qui avaient choisi le télétravail le mois précédent décident de continuer. Chaque mois 450 personnes supplémentaires choisissent le télétravail.
On modélise le nombre de personnes en télétravail par la suite (an). Ainsi a0 = 200.
Partie A.
1. Calculer a1.
a1 = 0,85 a0 +450 = 0,85 x200 +450 =620.
2. Justifier que an+1 = 0,85 an+450.
85 % des personnes qui avaient choisi le télétravail le mois précédent décident de continuer, c'est à dire 0,85 an.
. De plus chaque mois 450 personnes supplémentaires choisissent le télétravail.
3. On considère la suite (vn) définie par : vn = an-3000.
a. Montrer qu'il s'agit d'une suite géométrique de raison0,85.
vn+1 = an+1 -3000.
 an+1 = 0,85 an+450.
vn+1 =0,85 an+450-3000 = 0,85 an -2550 =0,85(an-3000) = 0,85 vn.
b. Exprimer vn en fonction de n.
vn = v0 0,85n.
v0 = a0-3000 = 200-3000 = -2800.
vn = -2800 x 0,85n
c En déduire que an = -2800 x 0,85n +3000.
an =vn+3000 =-2800 x 0,85n +3000.
4. Déterminer le nombre de mois au bout duquel le nombre de télétravailleurs sera  strictement supérieur à 2500.
-2800 x 0,85n +3000 > 2500.
2800 x 0,85n < 500.
0,85n < 5 /28 ; n ln(0,85) < ln(5 /28) ;
-0,1625 n < -1,723 ; n > 10,6 ( soit 11 mois).

 Partie B.
 Le nombre de personnes satisfaites par ce dispositif est modélisé par la suite (un) telle que : u0 = 1 et un+1=(5un+4) / (un+2)
un : nombre de milliers de personnes satisfaites de cette mesure au bout de n mois.
1. Démontrer que la fonction f définie sur [0 ; +oo[ par f(x) = (5x+4) /(x+2) est strictement croissante.
Calcul de f '(x) en posant u = 5x+4 et v = x+2 ; u' = 5 ; v' = 1.
(u'v-v'u) / v2 =( (5(x+2)-(5x+4)) / (x+2)2=6 / (x+2)2.
f '(x) étant strictement positive, f(x) est strictement croissante.
 2.a. Démontrer par récurrence que 0 <  un < un+1 < 4.
Initialisation : 0 <  1 < u1 < 3 est vraie.
Hérédité : la propriété est supposée vraie au rang n, c'est à dire : 0 <  un < un+1 < 4.
La fonction f étant strictement croissante et positive sur  [0 ; +oo[ et de plus la fonction tend vers f(4) = 5 quand x tend vers plus l'infini.
f(0) <  f(un )< f(un+1 )< f(5).
f(0) < un+1 < un+2 <  f(5).
2 < un+1 < un+2 <  4.
0 < un+1 < un+2 <  4.
La propriété est donc vraie au rang n+1.
Conclusion : la propriété est vraie au rang 1 et héréditaire, elle est vraie pour tout entier naturel n.
b. Justifier que cette suite converge.
La suite est croissante et majorée, donc elle converge.
3. On admet que 0 < 4-un < 3 x0,5n.
En déduire la limite de (un) et interpréter.
Quand n tend vers plus l'infini, 0,5n tend vers 0.
 0 < 4-un < 0.
D'après le théorème des gendarmes, un tend vers 4.
Au bout d'un temps suffisamment long, 4000 personnes sont satisfaites.

 Exercice 4.
Dans un repère orthonormé de l'espace, on considère les points :
A(2 ; -1 ; 0) ; B(3 ; -1 ; 2) ; C(0 ; 4 ; 1) et S(0 ; 1 ; 4).
1. Montrer que le  triangle ABC est rectangle en A.
AB2 = (3-2)2 +(-1+1)2 +(2-0)2) = 5.
AC2 =(0-2)2 +(4+1)2 +(1-0)2) = 30.
BC2 =(0-3)2 +(4+1)2 +(1-2)2) = 35.
BC2 = AB2 + AC2.
D'après la réciproque du théorème de Pythagore, le triangle ABC est rectangle en A.
 2.a. Montrer que le vecteur de coordonnées (2 ; 1 ; -1) est orthogonal au plan (ABC).

 b. En déduire une équation cartésienne de ce plan.
2x+y-z+d=0.
A appartient à ce plan : 2*2-1+0+d=0 soit d = -3.
2x+y-z-3=0.
c. Montrer que les points A, B, C et S ne sont pas coplanaires.
Si S appartient au plan (ABC) : 2xS+yS-zS-3 = 0.
2*0+1-4-3 = -6, différent de zéro.
Donc S n'appartient pas au plan (ABC).
 3. Soit (d) la droite orthogonale au plan(ABC) passant par S. Elle coupe le plan(ABC) en H.
a. Déterminer une représentation paramétrique de cette droite (d).
Le vecteur de coordonnées (2 ; 1 ; -1) est un vecteur directeur de (d) et de plus S appartient à cette droite :
x =2t+xS ; y = t+yS ; z = -t+zS avec t réel.
x = 2t ; y =t+1 ; z = -t+4.
b. Montrer que les coordonnées du point H sont H(2 ; 2 ; 3).
H appartient au plan (ABC) : 2xH+yH-zH-3=0.
H appartient à la droite (d) : xH = 2t ; yH =t+1 ; zH = -t+4.
4t+t+1+t-4-3 = 0 ; t = 1.
H(2 ; 2 ; 3).
4. Calculer le volume du tétraèdre SABC.
Aire du triangle ABC : AB x AC / 2 = (5 x30)½ / 2 = 2,5 x 6½.
Hauteur du tétraèdre SH =((2-0)2+(2-1)2+(3-4)2)½ =6½.
Volume du tétraédre SABC ; aire de base x hauteur / 3 =2,5 x 6½x6½/3 = 5 unités de volume.
5.a Calculer SA.
SA2 =(2-0)2+(-1-1)2 +(0-4)2 =24 ; SA = 2 x 6½.
b. On indique que SB = 17 ½.
En déduire une mesure de l'angle ASB approchée au dixième de degré.

  
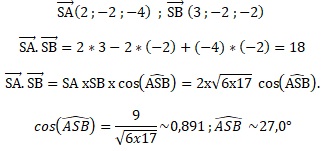
menu