Math�matiques,
fonction, probabilit�s, bac S M�tropole- La R�union 2020.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicit�s adapt�es � vos centres
d’int�r�ts.
..
..
|
.
.
|
..
..
......
...
|
Fonction.
On consid�re la fonction f d�finie sur R
par : f(x) = 2ex /(ex+1). On donne sa courbe repr�sentative.
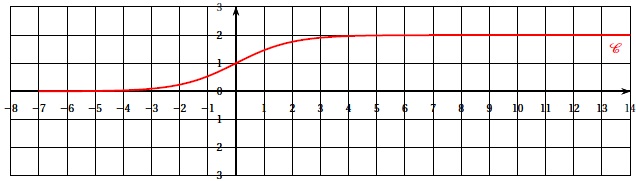1. Calculer la limite de f en moins l'infini
et interpr�ter le r�sultat.
Le terme ex
tend vers z�ro quand x tend vers moins l'infini.
f(x) tend donc vers z�ro
quand x tend vers moins l'infini.
L'axe des abscisses y = 0
est asymptote � la courbe.
2. Montrer que la droite d'�quation y = 2
est asymptote � la courbe.
f(x ) =2 / [ 1 +e-x]
.
Le terme e-x
tend vers z�ro quand x tend vers plus l'infini. f(x) tend vers 2 quand
x tend vers plus l'infini.
3. Calculer f '(x).
On pose u = ex,
v = 1+ex ; u' = ex
; v' = ex.
(u'v-v' u) / v2
= (ex( 1+ex)-e2x)
/ (1+ex)2 =ex /(1+ex)2
.
f '(x) = 2ex /(1+ex)2
.= f(x) / (1+ex).
4. Montrer que f
est croissante sur R.
ex et (1+ex)2
sont positifs sur R.
f '(x) �tant strictement positive, la fonction f(x) est strictement
croissante sur R.
5. Montrer que la
courbe passe par le point I (0 ; 1) et que la tangente � la courbe en I
a pour coefficient directeur 0,5.
Si le
point I appartient � la courbe, ces coordonn�es v�rifient :
f(0) =2 e0 /(1+e0) = 2 / 2 = 1 = yI.
Coefficient directeur de la tangente en ce point I : f '(0) = f(0) / (1+e0)= 1 /(1+1) = 0,5.
Une entreprise souhaite fabriquer des fl�tes ( verre � pied ) de forme
allong�e de contenance 12,5 cL.
A l'aide de la fonction f, le fabricant mod�lise le profil du contenant
de la fl�te.
Soit A un point de la courbe d'abscisse a > 0. La
rotation autour de l'axe des abscisses appliqu�e � la partie de
la courbe limit�e par les points A et i engendre une surface mod�kisant
le contenant de la fl�te en prenant pour unit� 1 cm. L'objectif est de
d�terminer a pour que le volume soit de 12,5 cL.
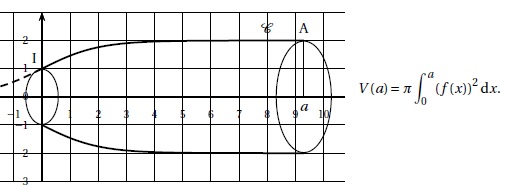
1. V�rifier, pour
tout r�el x > 0, l'�galit� : (f(x))2 =4 [ ex/(1+ex)
+(-ex) / (1+ex)2].
[ ex/(1+ex)
+(-ex) / (1+ex)2] = [ ex
(1+ex) / (1+ex)2 +(-ex)
/ (1+ex)2] = [ ex
(1+ex) +(-ex)]
/ (1+ex)2.
(e2x+ex-ex) / (1+ex)2=
e2x
/ (1+ex)2=
f(x)2 / 4.
2. D�terminer une
primitive de chacune des fonctions : g(x) =ex
/ (1+ex) et h(x) = -ex
/(1+ex)2.
On pose u = ex +1 ; u' = ex ; g(u) = u' / u.
Primitive de g(x) :G(x) = ln(u) = ln(1+ex).
On pose w =( ex +1) ; w ' = ex
; h(w) = - w' / w2 .
Primitive de h(x) : H(x) = 1 / ( ex +1).
3. En d�duire que
pour tout r�el a >
0 : V(a) = 4 p[ ln(1+ea) / 2 + 1 /(ea+1)
-0,5]
V(a) =4 p [G(a) -G(0) -0,5(
H(a)-H(0)]
V(a) =4 p
[ln(1+ea) -ln(2) + 1/ (1+ea)-0,5)].
V(a) =4 p ([ln(1+ea)/2)+
1/ (1+ea)-0,5)].
4. D�terminer a �
l'aide de la calculatrice. 12,5 cL = 125 cm3.
V(11,1) = 124,4 ; v(11,2) = 125,6) ; a ~11,1 cm.
Un client commande un lot de 400 fl�tes. et constate que 13
d'entre elles ne sont pas conformes aux caract�ristiques annonc�es. Le
responsable commerciale affirme que 98 % des fl�tes sont conformes.
Le lot du client permet-il au risque de 5 % de mettre en doute
l'affirmation du commercial ?
n =400 ; p = 0,98 ; n >
30 ; np =400 x0,98 =392 >
5 ; n(1-p) = 400 x0,02 = 8 >
5.
[p(1-p) / n ]� =[0,98 x0,02
/ 400 ]� =7 10-3.
1,96 x7 10-3 ~0,0137.
Intervalle de fluctuation asymptotique au seuil de 95 % :
[0,98 -0,0137 ; 0,98 +0,0137) soit : [ 0,966 ;0,994 ].
Fr�quence observ�e : (400-13) / 400 =0,9675.
Cette valeur appartient � l'intervalle de confiance. L'affirmation ne
peut pas �tre remise en cause.
|
...
|
....
|
Probabilit�s.
Une
machine fabrique des boules destin� � un jeu de hasard. La masse d'une
boule peut �tre mod�lis�e par une variable al�atoire M suivant une loi
normale d'esp�rance 52 et d'�cart type s. Les boules dont la masse est comprise entre 51 et 53 g sont dites conformes.
1. Avec
les r�glages initiaux de la machine, on a s = 0,437. Calculer la
probabilit� qu'une boule soit conforme. Donner une valeur approch�e � 10-1 pr�s.
Partie A.
La calculatrice ou les tables donnent : P(M <51)=0,01106 ; P(M <53)=0,99894 ;
P ( 51 < M < 53)= 0,99894 -0,01106 =0,988 ~1.
2. On consid�re que
la machine est correctement r�gl�e si au moins 99 % des boules qu'elle
fabrique sont conformes. D�terminer une valeur approch�e de s qui permette d'affirmer que la machine est correctement r�gl�e.
On pose Z =(M-52) / s ; Z suit la loi normale centr�e r�duite N(0 ; 1).
P ( 51 < M < 53) =0,99 ; P ( 51-52 < M -52< 53-52) > 0,99 ;
P ( -1 < M -52< 1) > 0,99 ; P ( -1/ s < Z < 1/ s) > 0,99 ;
2 P(Z < 1/ s)-1 > 0,99 ; 2 P(Z < 1/ s) > 1,99 ; P(Z < 1/ s) > 0,995.
La calculatrice donne : 1 / s > 2,576 ; s < 0,388.
Partie B.
La pes�e de boules se fait sur une balance �lectronique pr�cise. Chaque
jour on v�rifie que la balance n'est pas d�r�gl�e. La dur�e, un jour,
de l'utilisation de ces balances avant des r�glements est mod�lis�e par
une variable al�atoitre T qui suit une loi exponentielle de param�tre l. La courbe repr�sentative de la fonction densit� de cette variable T est repr�sent�e ci-dessous.
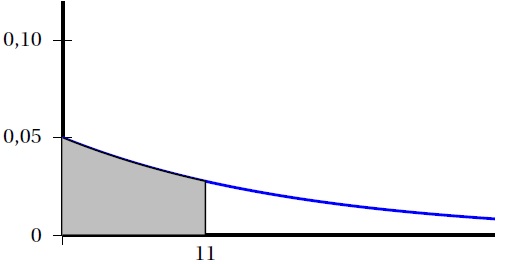
1.a Par lecture graphique, donner un encadement de l d'amplitude 0,01.
Fonction de densit� de cette variable T : f(x) = l exp(-lt). f(0) = l ;
Le graphique indique : 0,04 < l < 0,06.
1.b. L'aire du domaine gris� est �gal � 0,45. D�terminer la valeur exacte de l.
P(X < 11 ) = 1-exp(-11 l) = 0,45 ; exp(-11 l) = 0,55.
-11 l= ln(0,55) ; l= -ln(0,55) / 11~0,054.
2. D�terminer, � un jour pr�s, la dur�e d'utilisation d'une balance sans qu'elle ne se d�r�gle.
Esp�rance de la variable T : 1 / l = 1 / 0,054 ~18,51 ( 19 jours).
3. Une balance est mise en service le 1er janvier 2020. Elle fonctionne sans se d�r�gler du 1er au 20 janvier inclus.
D�terminer la probabilit� qu'elle fonctionne jusqu'au 31 janvier inclus.
Cette loi exponentielle est � dur�e de vie sans vieillissement.
P T > 20 ( T > 31) =P (T > 11) = 1 -T < 11) =1 -0,45 = 0,55.
Partie C.
On dispose de deux urnes U et V contenant des boules fabriqu�es comme
pr�c�demment. Sur chaque boule est inscrit un nombre -1, 1 ou 2.
L'urne U contient une boule portant le nombre 1 et trois boules portant le nombre -1.
L'urne V contient une boule portant le nombre 1 et trois boules portant le nombre 2.
On consid�re un jeu dans lequel chaque partie se d�roule de la mani�re suivante :
on tire au hasard une boule dans l'urne U, on note x le nombre inscrit sur cette boule puis on la remet dans l'urne V.
Dans un deuxi�me temps, on tire au hasard une boule dans l'urne V et on note y le nombre inscrit sur cette boule.
On consid�re les �v�nements suivants :
U1 : on tire une boule dans l'urne U portant le nombre 1 ( x = 1).
U-1 : on tire une boule dans l'urne U portant le nombre -1 ( x = -1).
V1 : on tire une boule dans l'urne V portant le nombre 1 ( y = 1).
V2 : on tire une boule dans l'urne V portant le nombre 2 ( y = 2).
V-1 : on tire une boule dans l'urne V portant le nombre -1 ( y = -1).
1. Compl�ter l'arbre pond�r� repr�sent� ci-dessous.
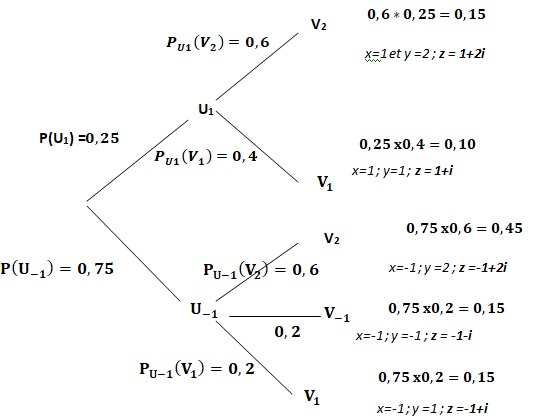
2. Dans ce jeu, on associe � chaque partie le nombre complexe z = x +iy. Calculer les probabilit�s des �v�nements suivants :
A : z = -1-i ; P(A) =0,15.
B : z est solution de l'�quation t2 +2t+5=0.
Discriminant D = 22-4*5 = -16 = 16 i2 =(4i)2.
Solutions : (-2 +4i) / 2 = -1+2i et (-2-4i) / 2 = -1-2i.
z = -1+2i et z =-1-2i ; P(B) =0,45.
C : Dans le plan complexe, le point M d'affixe z appartient au disque de centre O et de rayon 2.
Equation du cercle x2 +y2 = 4.
Si x = �1 et y = �1; 1 +1 diff�re de 4.
Si x = �1 et y = 2; 1 +4 diff�re de 4.
P(C) = 0.
3. Lors d'une
partie, on obtient le nombre 1 sur chacune des boules tir�es. Montrer
que le nombre complexe z associ� � cette partie v�rifie :
z2020 = -21010.
z = 1+i ; |z| = (12 +12)� = 2�.
z = 1 /2� +i /2� = cos ( p/4) + i sin (p/4) ; z = 2� exp ( i p/4).
z2020 =21010 exp ( i p/4*2020) =21010 exp ( i p * 505) =21010 exp ( i p * (2*252+1)) =21010 exp ( i p )= -21010.
|
|
