Spécialité
mathématiques,
bac général 2021.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
..
..
|
|
Exercice 1. 5 points.
Dans une école, après étude des dossiers des candidats, le recrutement se fait de deux façons :
10 % des candidats sont sélectionner sur dossier. Ils doivent ensuite
passer un oral à l'issue duquel 60 % sont finalement admis.
Les autres candidats passent une épreuve écrite à l'issue de laquelle 20 % d'entre eux sont admis à l'école.
Partie 1.
On choisit au hasard un candidat à ce concours de recrutement. On note les événements :
D: candidat sélectionné sur dossier ;
A : candidat admis à l'école.
1. Traduire la situation sur un arbre pondéré.
2. Calculer la probabilité que le candidat soit sélectionné sur dossier et admis.
3. Montrer que P(A) = 0,24.
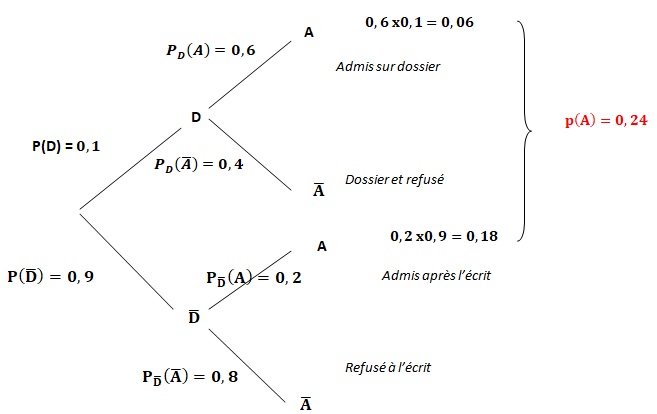
4. On choisit au hasard un candidat admis à l'école. Quelle est la probabilité que son dossier n'ait pas été sélectionné ?
P A non D =P(A n non D) / P(A) = 0,18 / 0,24 =0,75.
Partie 2.
1. on
admet que la probabilité pour un candidat d'être admis à l'école est
égale à 0,24. On considère un échantillon de 7 candidats choisis au
hasard, en assimilant ce choix à un tirage au sort avec remise. On
désigne par X la variable aléatoire dénombrant les candidats admis à
l'école parmi les 7 tirés au sort.
a. On admet que X suit une loi binomiale. Quels sont les paramètres de cette loi ?
n = 7 ; p = 0,24.
b. Calculer la probabilité qu'un seul des sept candidats tirés au sort soit admis à l'école.
P(X = 1) =0,32.
c. Calculer la probabilité qu'au moins deux des sept candidats tirés au sort soient admis à cette école.
P(X > 2) = 1-P(X=0) -P(X=1) = 1-0,146-0,324 ~0,53.
2. Un lycée présente n candidats au recrutement dans cette école, où n est un entier non nul.
a. Donner l'expression, en fonction de n, de la probabilité qu'aucun candidat issu de ce lycée ne soit admis à l'acole.
P(X=0)= Cn0 p0 qn avec C200 = 1 ; P(X=0)= (1-0,24)n =0,76n.
b.
A partir de quelle valeur de l'entier n la probabilité qu'au moins un
élève de ce lycée soit admis à l'école est-elle supérieure ou égale à
0,99 ?
P(X >1)=1-P(X=0) =0,99 ; 1-0,76n = 0,99 ; 0,01 =0,76n ; ln(0,01) = n ln(0,76) ; n = ln(0,01) / ln(0,76) ~17.
Exercice 2. 5 points.
Soit f la fonction définie sur ]0 ; +oo[ par f(x) = ex / x. On note C la courbe représentative de f.
1.a. Préciser la limite de f en +oo.
Par croissance comparée f(x) tend vers +oo quand x tend vers +oo.
b. Justifier que l'axe des ordonnées est asymptote à la courbe C.
Quand x tend vers zéro f(x) tend vers plus l'infini ; l'axe des ordonnées est asymptote à la courbe C.
2. Montrer que f '(x) =ex(x-1) / x2.
on pose u = ex et v = x ; u' = ex et v' = 1.
(u'v-v'u) / v2 =(xex-ex) / x2 = ex(x-1) /x2.
3. Déterminer les variations de la fonction f.
ex et x2 étant positifs, f '(x) a le signe de x-1.
Si x < 1, f '(x) < 0 et f(x) est décroissante.
Si x > 1, f '(x) >0 et f (x) est croissante.
Si x = 1 f '(x) =0 et f(x) présente un minimum égal à e.
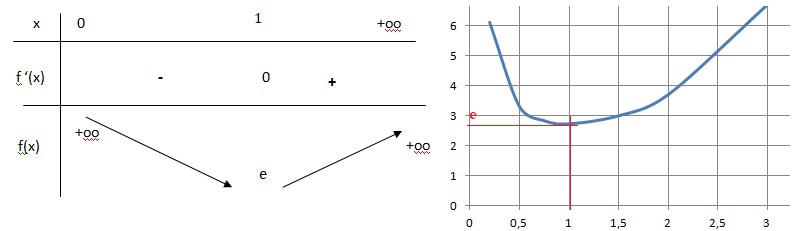
4. Soit m un nombre réel. Préciser, en fonction des valeurs de m, le nombre de solutions de l'équation f(x) = m.
Si m < e, aucune solution.
Si m = e, une solution unique.
Si m > e, deux solutions.
5.
On note D la droite d'équation y = -x. On note A un éventuel point de C
d'abscisse a en lequel la tangente à la courbe C est parallèle à la
droite D.
a. Montrer que a est solution de l'équation ex(x-1)+x2=0.
Coefficient directeur de la tangente à C au point A : -1 = f '(a) =ea(a-1) / a2.
ea(a-1) = -a2 ; ea(a-1) +a2 =0.
On note g la fonction définie sur ]0 ; +oo[ par g (x) = ex(x-1)+x2.
b. Calculer g'(x) puis dresser le tableau de variations de g.
On pose u = ex et v = x+1 ; u' = ex ; v' = 1 ; u'v+v'u =ex(x-1)+ex=xex.
g'(x) = xex+2x = x(ex+2) strictement positive sur ]0 ; +oo[.

c. Montrer que le point A est unique.
La courbe représentative de g(x) coupe l'axe des abscisses en un seul point. L'équation ex(x-1)+x2=0 admet une seule solution.
Exercice 3 QCM. 5 points.
Aucune justification n'est demandée ; une seule réponse est vraie.
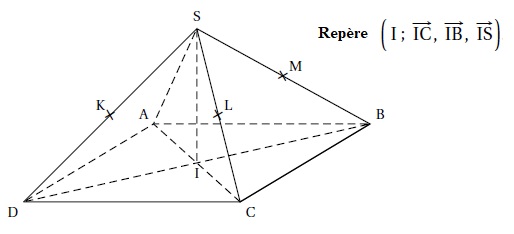
SABCD
est une pyramide à base carrée ABCD dont toutes les arètes ont la même
longueur. I est le centre du carré ABCD. IC=IB=IS=1. Les points K, L et
M sont les milieux des arêtes respectives [SD], [SC] et [SB].
1. Les droites suivantes ne sont pas coplanaires :
(DK et (SK) faux, elles ont le point K en commun.
(AS) et (IC) faux, elles ont le point A en commun.
(AC) et (SB). Vrai. Les points A, C et B appartiennent au plan (ABC) et S est en dehors de ce plan.
(LM) et (AD), faux, elles sont parallèles et appartiennent au plan ADLM.
On donne les coordonnées des points I(0 ; 0 ; 0) ; A(-1 ; 0 ; 0) ; B(0 ; 1 ; 0) ; C(1 ; 0 ; 0) ; D(0 ; -1 ; 0) ; S(0 ; 0 ; 1).
2. Les coordonnées du milieu N de [KL] sont :
K milieu de [SD] ; K(0 ; -0,5 ; 0,5) ; L milieu de [SC] ; L(0,5 ; 0 ; 0,5) ;
N( 0,25 ; -0,25 ; 0,5) ; réponse B.
3. Les coordonnées du vecteur 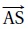 sont : sont :
xS-xA =1 ; yS-yA =0 ; zS-zA =1 ; réponse B.
4. Une représentation paramétrique de la droite (AS) est :
x = t+xS ; y = yS et z = t+zS avec t réel ;
x = t ; y = 0 ; z = t+1 ; réponse C.
5. Une équation cartéienne du plan (SCB) est :
ax+by+cz+d=0
S appartient à ce plan : c+d = 0 ;
C appartient à ce plan : a+d = 0 ; soit a = c = -d ;
B appartient à ce plan : b+d = 0 ; b = -d.
Par suite : a = b = c = -d ; équation de ce plan : x+y+z-1=0 ; réponse B.
|
|
4. A. Au choix. 5 points.
La suite (un) est définie par u0 = 1 et pour tout entier n, un+1 = 0,75 un +0,25n+1.
1. Calculer en détaillant u1 et u2.
u1 =0,75 +0,25 x0+1 = 1,75 = 7 /4.
u2 =3 /4 x 7 / 4 +0,25 x1+1 = 21 / 16 +1 / 4 +1 =(21+4+16) / 16 =41 / 16.
Le tableau suivant est extrait d'une feuille de calcul
|
A
|
B
|
1
|
n
|
un
|
2
|
0
|
1
|
3
|
1
|
1,75
|
4
|
2
|
2,5625
|
5
|
3
|
3,421 875
|
6
|
4
|
4,316 406 25
|
2.a Quelle formule, étirée ensuite vers le bas, peut-on écrire en B3 pour obtenir les termes successifs de (un) ?
=0,75*B2+0,25*A2+1
b. Conjecturer du sens de variation de la suite.
La suite est croissante.
3.a Démontrer par récurence : n < un < n+1.
Initialisation : 0 < u0 < 1 est vraie.
Hérédité : n < un < n+1 est supposée vraie.
0,75 n < 0,75 un < 0,75(n+1).
0,75 n+0,25 n < 0,75 un +0,25n < 0,75(n+1)+0,25 n ; n < 0,75 un +0,25n < n+0,75 ;
n+1 < 0,75 un +0,25n +1< n+0,75 +1 ; n+1 < un+1 < n+1,75.
n+1 < un+1 < n+2. La propriété est vraie au rang n+1.
La propriété est vraie au rang 1 et héréditaire, elle est vraie pour tout entier naturelle n.
b. En déduire en justifiant le sens de variation et la limite de cette suite.
un+1 -un = 0,75 un -un+0,25n+1 = -0,25 un +0,25 n+1 ;
0,25un < 0,25n+0,25 ; 0,25un < 0,25n+1 ; un+1 -un >0, la suite est croissante. La suite (un) tend vers plus l'infini.
c. Démontrer que la limite en plus l'infini de un / n = 1.
n < un < n+1 ; 1 < un / n < 1+1 / n ; la limite en plus l'infini de un / n = 1.
4. On désigne par (vn) la suite définie sur N par vn = un-n.
a. Démontrer que la suite (vn) est géométrique de raison 0,75.
vn+1 = un+1 -(n+1)=0,75 un +0,25n+1-n-1 =0,75 un-0,75 n = 0,75(un-n) = 0,75 vn.
Suite géométrique de raison 0,75 et de premier terme v0 =u0=1.
b. En déduire que un = 0,75n+n.
vn = 0,75n =un-n ; un = 0,75n+n.
Exercice B. Au choix.
On considère la fonction f définie sur ]0 ; +oo[ par f(x) =x+4-4ln(x)-3 /x. On note C sa courbe représentative.
1. Déterminer la limite de f en plus l'infini.
f(x / x =1+4/ x-4ln(x) / x -3 /x2. 4 / x tend vers zéro ; 4ln(x) / x tend vers zéro ; 3 /x2 tend vers zéro ; f(x / x tend vers 1 ; f(x) tend vers plus l'infini.
2. Montrer que f '(x) =(x2-4x+3) / x2.
f '(x) =1-4 /x+3 /x2 =(x2-4x+3) / x2.
3. a. Donner le tableau de variation de f.
f '(x) a le signe de x2-4x+3.
On cherche les solutions de x2-4x+3 = 0 ; discriminant D =42-3*4 = 4 = 22.
x1 = (4+2) / 2 = 3 ; x2 = (4-2) / 2=1.
x2-4x+3 < 0 sur ]1 ; 3[ et la fonction est strictement décroissante.
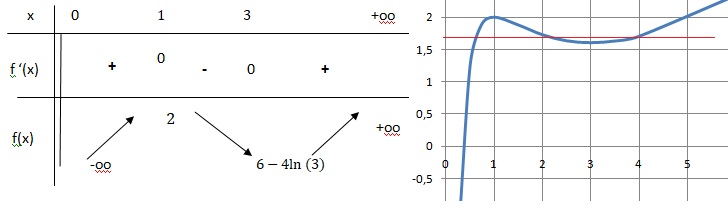
b. Par simple lecture du tableau de variations, préciser le nombre de solutions de l'équation f(x) = 5 /3.
6-4ln(3) ~1,605 ; 5 / 3 ~1,66; doncf(x) = 5 /3 admet 3 solutions.
4. Etudier la
convexité de la fonction f. Justifier que la courbe C admet un unique
point d'inflexion dont on précisera les coordonnées.
f '(x) =(x2-4x+3) / x2.
Calcul de la dérivée seconde f "(x) en posant :
u = x2-4x+3 , v = x2. u' = 2x-4 ; v' = 2x.
(u'v-v'u) / v2 =((2x-4)x2 -2x(x2-4x+3)) / x4 = (4x2-6x) / x4 =2x(2x-3) /x4 .
Sur ]0 ; +oo[, f "(x) s'annule et change de signe pour x = 1,5 ; f(1,5) =3,5 - 4 ln(1,5) ~1,88.
f "(x) >0 pour x > 1,5, f(x) convexe.
f "(x) < 0 pour x < 1,5, f(x) concave.
|
|




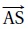 sont :
sont :