Math�matiques, fonction, g�om�trie, probabilit�s, bac septembre 2021.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicit�s adapt�es � vos centres d’int�r�ts.

.. ..


.
.
.. ..
......


...
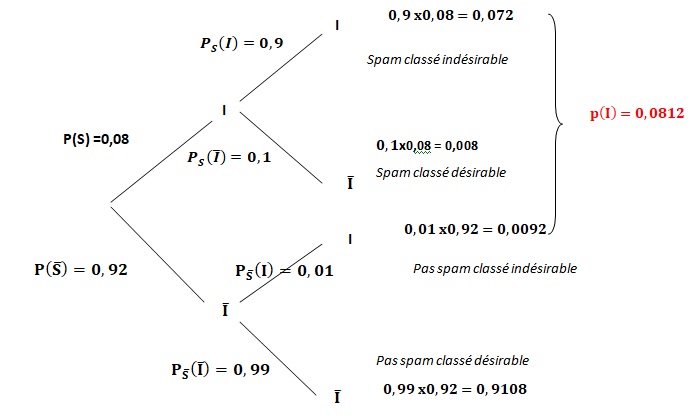
Probabilit�s. 4 points
Une entreprise re�oit quotidiennement de nombreux courriels (courriers �lectroniques).
Parmi ces courriels, 8% sont du � spam�, c’est-�-dire des courriers � intention publicitaire, voire malveillante, qu’il est souhaitable de ne pas ouvrir.
On choisit au hasard un courriel re�u par l’entreprise.
Les propri�t�s du logiciel de messagerie utilis� dans l’entreprise permettent d’affirmer que :
• La probabilit� que le courriel choisi soit class� comme � ind�sirable � sachant que c’est un spam est �gale � 0,9.
• La probabilit� que le courriel choisi soit class� comme � ind�sirable � sachant que ce n’est pas un spam est �gale � 0,01.
On note :
• S l’�v�nement � le courriel choisi est un spam�;
• I l’�v�nement � le courriel choisi est class� comme ind�sirable par le logiciel de messagerie �.
1. Mod�liser la situation �tudi�e par un arbre pond�r�, sur lequel on fera appara�tre les probabilit�s associ�es � chaque branche.
2. a. D�montrer que la probabilit� que le courriel choisi soit un messagede spam et qu’il soit class� ind�sirable est �gale � 0,072.
b. Calculer la probabilit� que le message choisi soit class� ind�sirable.

c. Le message choisi est class� comme ind�sirable. Quelle est la probabilit� que ce soit effectivement un message de spam ? On donnera un r�sultat arrondi au centi�me.
PI(S) = P(I n S) / P(I) =0,072 / 0,0812 ~0,89.
3. On choisit au hasard 50 courriels parmi ceux re�us par l’entreprise. On admet que ce choix se ram�ne � un tirage au hasard avec remise de 50 courriels parmi l’ensemble des courriels re�us par l’entreprise.
On appelle Z la variable al�atoire d�nombrant les courriels de spam parmi les 50 choisis.
a. Quelle est la loi de probabilit� suivie par la variable al�atoire Z, et quels sont ses param�tres ?
On choisit 50 courriels de mani�re ind�pendante. Deux issues sont possibles " le courriel n'est pas un spam " ou" le courriel est un spam".
On r�p�te 50 fois une �preuve de Bernoulli.
Z suit une loi binomiale de param�tre n =50 ; p = 0,08.
b. Quelle est la probabilit� que, parmi les 50 courriels choisis, deux au moins soient du spam ? On donnera un r�sultat arrondi au centi�me.
P(Z >2) = 1 -P(Z < 1) =1-0,083 ~0,92.
QCM. 5 points.
Dans l’espace rapport� � un rep�re orthonorm� on consid�re les points A(1; 0; 2), B(2; 1; 0), C(0; 1; 2) et la droite D dont une repr�sentation param�trique est :
 x = 1+2t
y = −2+t
z = 4−t
avec t r�el.
1. Parmi les points suivants, lequel appartient � la droite D ?
R�ponse A  :M(2 ; 1 ; −1) ; R�ponse B : N(−3 ; −4 ; 6) ; vrai.
R�ponse C : P(−3 ; −4 ; 2) ; R�ponse D : Q(−5 ; −5 ; 1).
Si M appartient � la droite D : 2 = 1+2t ; t = 0,5.
alors yM =-2 +0,5 = -1,5 diff�rent de 1.( M n'appartient pas � D).
Si N appartient � la droite D : -3 = 1+2t ; t = -2.
alors yN =-2 -2 = -4 et zN =4 +2 = 6.( N appartient � D).

2. Le vecteur AB a pour coordonn�s :
R�ponse A : (1,5 ; 0,5 ; 1). R�ponse B : (-1 ; -1 ; 2).
R�ponse C : (1 ; 1 ; -2). R�ponse D : (3 ; 1 ; 2).
xB-xA = 2-1 = 1 ; yB-yA = 1-0 = 1 ; zB-zA = 0-2 = -2 ; R�ponse C.

3. Une repr�sentation param�trique de la droite (AB) est :
R�ponse A : (x = 1+2t ; y =t ; z=2 ). R�ponse B : (x=2-t ; y=1-t ; z=2t).
R�ponse C : (x=2+t ; y=1+t ; z=2t). R�ponse D : (x =1+t ; y=1+t ; z=2-2t) avec t r�el.
Le vecteur BA de coordonn�es (-1 ; -1 ; 2) est un vecteur directeur de cette droite :
B(2 ; 1 ; 0) appartient � cette droite : x = -t+xB ; y = -t+yB ; z = 2t+zB ; x = -t+2 ; y =- t+1 ; z =2t. R�ponse B.

4. Une �quation cart�sienne du plan passant par le point C et orthogonal � la droite D est :
R�ponse A : x −2y +4z −6 = 0; R�ponse B : 2x + y −z +1 = 0;
R�ponse C : 2x + y −z −1 = 0; R�ponse D : y +2z −5 = 0.
Coordonn�s d'un vecteur ortogonal � ce plan  ( vecteur directeur de la droite D) : 2  1 ; -1.
Equation cart�sienne de ce plan :2x+y-z+d=0.
C(0 ; 1 ; 2) appartient � ce plan : 0 +1-2+d=0 soit d = 1. R�ponse B.

5. On consid�re le point D d�fini par la relation vectorielle suivante :


...
....

 Fonction (6 points).
Partie I.
On consid�re la fonction f d�finie sur R par f (x) = x −e−2x .
On appelle G la courbe repr�sentative de la fonction f dans un rep�re orthonorm�.
1. D�terminer les limites de la fonction f en −∞et en +∞.
En plus l'infini : e-2x tend vers z�ro et f(x) tend vers plus l'infini.
En moins l'infini, e-2x tend vers plus l'infini ;  -e-2x tend vers moins l'infini et f(x) tend vers moins l'infini.
2. �tudier le sens de variation de la fonction f sur R et dresser son tableau de variation.
 f '(x) = 1 +2e-2x > 0 ; f(x) est strictement croissante.

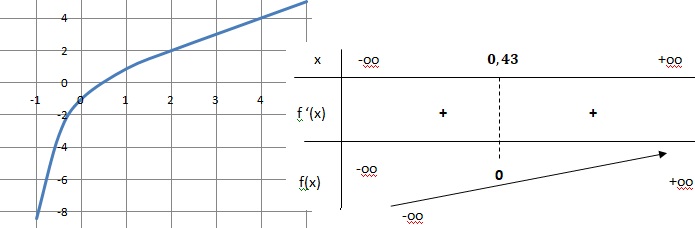
3. Montrer que l’�quation f (x) = 0 admet une unique solution α sur R, dont on donnera une valeur approch�e � 10−2 pr�s.
Dapr�s le tableau de variation pr�c�dent ( ou d'apr�s le th�or�me de la bijection), f (x) = 0 admet une unique solution α sur R
4. D�duire des questions pr�c�dentes le signe de f (x) suivant les valeurs de x.
f(x) < 0 si x appartient � ]-oo ; a[ ;
f(x) > 0 si x appartient ] a ; +oo[ ;
f(a) = 0.

 Partie II
Dans le rep�re orthonorm�, on appelle C la courbe repr�sentative de la fonction
g d�finie sur R par : g(x) = e−x .
La courbes C et la courbe G (qui repr�sente la fonction f de la Partie I) sont trac�es
Le but de cette partie est de d�terminer le point de la courbe C le plus proche de l’origine O du rep�re et d’�tudier la tangente � C en ce point.
1. Pour tout nombre r�el t , on note M le point de coordonn�es (t ; e−t ) de la courbe C .
On consid�re la fonction h qui, au nombre r�el t , associe la distance OM.
On a donc : h(t )=OM, c’est-�-dire : h(t )=(t 2+e−2t)�.
a. Montrer que, pour tout nombre r�el t ,
h′(t ) =f(t) / (t2+e−2t)�
o� f d�signe la fonction �tudi�e dans la Partie I.
On pose u = t2+e−2t ; u' = 2t-2e-2t.
h(u) = u� ; h'(u) = �u' u-�.
h'(t) =( t-e-2t) / (t2+e−2t)� = f(t) / (t2+e−2t)� .
 b. D�montrer que le point A de coordonn�es (α ; e−α) est le point de la courbe C pour lequel la longueur OM est minimale.
Placer ce point sur le graphique donn�.
h'(t) < 0 si t appartient � ]-oo ; a[ et h(t) est d�croissante.
h'(t) >0 si t appartient � ] a ; +oo[ et h(t) est croissante.
h'(t) = 0 si t = a et h(t) est minimale.

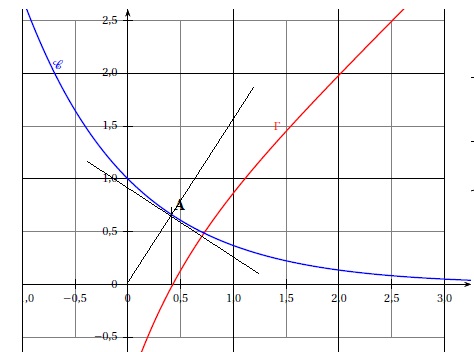
2. On appelle T la tangente en A � la courbe C .
a. Exprimer en fonction de α le coefficient directeur de la tangente T .
g'(a)= -e-a.
On rappelle que le coefficient directeur de la droite (OA) est �gal � e−α / α.
On rappelle �galement le r�sultat suivant qui pourra �tre utilis� sans d�monstration.:
Dans un rep�re orthonorm� du plan, deux droites D et D′ de coefficients directeurs
respectifs m et m′ sont perpendiculaires si, et seulement si le produit mm′ est �gal � −1.
b. D�montrer que la droite (OA) et la tangente T sont perpendiculaires.
Tracer ces droites sur le graphique donn�.
g'(a) e−α / α = -e−2α / α ;
or f (a) = a −e−2a  = 0 ; e−2a  =a ;
g'(a) e−α / α =-1. La droite (OA) et la tangente T sont donc perpendiculaires.

  
menu