CESTA
PUNTA, mouvement dans un champ de pesanteur uniforme, �nergie, bac
septembre 2021.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicit�s adapt�es � vos centres
d’int�r�ts.
..
..
|
.
.
|
..
..
......
...
|
La
pelote basque est un sport de balle se pratiquant � main nue, avec une
raquette en bois ou avec un chistera (gant en osier). La
cesta punta est une des sp�cialit�s de la pelote basque. Le jeu
consiste � renvoyer la balle servie par l’adversaire avec un chistera
sur le mur appel� le fronton.
Le service s’effectue sur un terrain rectangulaire sur lequel des
lignes de r�f�rence sont trac�es. Le service s’effectue � 36 m�tres du
mur, il est r�ussi lorsque la balle, apr�s avoir rebondi contre le mur,
retombe entre les lignes 4 et 7.
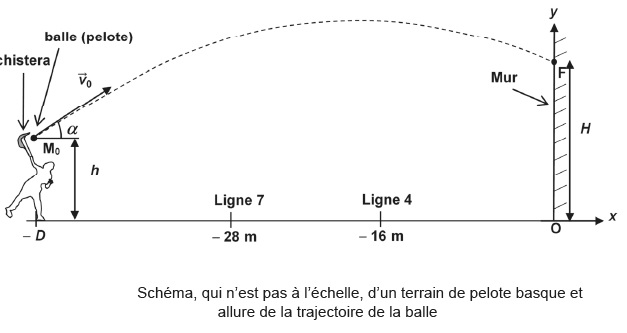
Dans le r�f�rentiel terrestre suppos� galil�en muni du rep�re (Ox ;
Oy), une balle suppos�e ponctuelle est envoy�e par un joueur depuis un
point M0 de coordonn�es x0 = -D et y0 = h. Gr�ce � son chistera, le joueur lance la balle � une vitesse initiale de norme v0 dont le vecteur v0
forme un angle α avec l’horizontale. Le mouvement de la balle
s’effectue dans le champ de pesanteur ; on n�glige l’influence de l’air.
Le moment o� la balle quitte le chistera est choisi comme origine des dates : t0 = 0 s.
Le but de cet exercice est d’�tudier, � l’aide du mod�le de la chute
libre, le mouvement de la balle afin de pr�voir si le service est
r�ussi. Le mouvement est d�compos� en deux phases : avant puis apr�s le
rebond sur le mur.
Donn�es :
D = 36 m ;
masse de la balle : m = 126 g ;
valeur mesur�e � l’aide d’un radar de la vitesse initiale de la balle : v0 = 36,2 m�s-1 ;
α = 12� ;
intensit� de la pesanteur : g = 9,81 m�s-2.
1. Mouvement de la balle avant le rebond sur le mur.
1.1. Indiquer
l’information de l’�nonc� permettant de formuler l’hypoth�se que le
mouvement de la balle s’effectue dans le cadre du mod�le de la chute
libre.
" on n�glige l’influence de l’air".
En absence de frottements, la balle n'est soumise qu'� son poids.
1.2. En appliquant la deuxi�me loi de Newton, montrer que l’�quation horaire du mouvement de la balle selon l’axe Ox est :
x(t) = v0 � cos(α) t - D.
Coordonn�es du vecteur acc�l�ration : 0 ; -g.
Vecteur vitesse initiale : v0 � cos(α) ; v0 � sin(α)
Le vecteur vitesse est une primitive du vecteur acc�l�ration : vx = v0 � cos(α) ; vy = v0 � sin(α) -gt.
Vecteur position initiale : -D ; h.
Le vecteur position est une primitive du vecteur vitesse : x = v0 � cos(α) t - D.
1.3. Montrer que la balle frappe le mur � la date tF = 1,0 s.
0=36,2 x cos(12) tF-36 ; 0 = 35,4 tF-36 ; tF = 36 /35,4 =1,0 s.
2. �tude �nerg�tique de la balle avant le rebond sur le mur.
2.1. Rappeler les expressions litt�rales de l’�nergie cin�tique Ec, de l’�nergie potentielle de pesanteur Epp et de l’�nergie m�canique Em
de la balle. L’�nergie potentielle de pesanteur est choisie nulle �
l’ordonn�e y = 0 m. On note v la norme du vecteur vitesse de la balle.
Ec = �mv2 ; Epp = mgy ; Em = �mv2 +mgy.
2.2. Calculer la valeur de l’�nergie cin�tique Ec � la date t = 0 s.
�mv02 = 0,5 x0,126 x36,22~82,6 J.
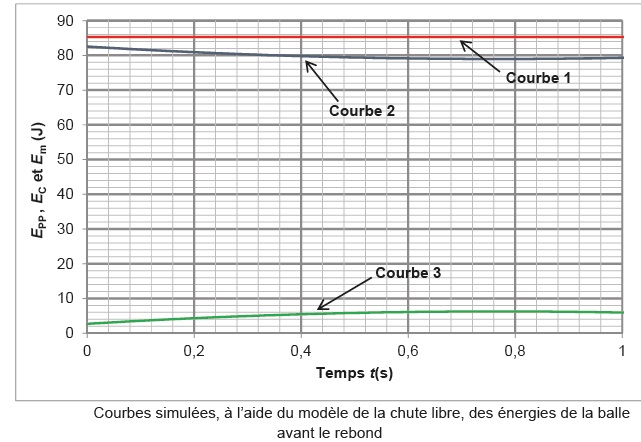
2.3. En explicitant votre raisonnement, identifier pour chaque courbe de la figure 2 la forme d’�nergie correspondante.
Courbe 3 : l'�nergie pottentielle de pesanteur cro�t, passe par un maximum, puis d�cro�t.
Courbe 2 : l'�nergie cin�tique ( 52,6 J initialement ) d�cro�t, passe par un minimum, puis cro�t.
Courbe 1 : �nergie m�canique constante ( absence de frottements) , somme des �nergies cin�tique et potentielle.
2.4. � l’aide de la figure 2, �valuer la valeur de la hauteur H de la balle lorsqu’elle touche le mur au point F.
Epp = 6 J.
6 = mgy ; 6 = 0,126 x9,81 y ; y =6 / 1,236 = 4,9 m.
|
...
|
....
|
3. Mouvement de la balle apr�s le rebond sur le mur.
La balle rebondit sur le mur en F. On fait l’hypoth�se que la balle repart � la vitesse vF = 35 m�s–1.
L’instant du rebond est choisi comme nouvelle origine des dates dans cette partie.
La balle, apr�s avoir rebondi contre le mur, doit retomber entre les
lignes 4 et 7 pour que le service soit r�ussi. Si la ligne 4 n’est pas
d�pass�e, le point est acquis � l’adversaire. Si la ligne 7 est
d�pass�e, le joueur a droit � un second et dernier service.
Le mouvement de la balle est �tudi� dans le r�f�rentiel terrestre
suppos� galil�en muni du rep�re (Ox ; Oy) d�fini sur la figure 1.
L’�tude de ce mouvement permet d’�tablir les �quations horaires de la
balle :
x(t) = – 34,9 t et y(t) = – 4,9 t 2 – 2,4 t + 4,9
avec x et y exprim�s en m�tre et t en seconde.
3.1. �valuer la valeur de la vitesse vF � partir des �quations horaires de la balle. Comparer avec la valeur donn�e ci-dessus.
vx(t)= -34,9 ; vy(t) =-9,8t-2,4.
vx(t=0)= -34,9 ; vy(t=0) =-2,4.
v= (vx2 + vy2)� =((-34,9)2 + (-2,4)2)� ~35 m /s, en accord avec la valeur donn�e.
3.2. Interpr�ter la valeur du coefficient du terme en t2 dans l’expression de y(t). Pr�ciser son unit�.
Acc�l�ration de la pesanteur / 2, exprim�e en m s-2.
� l’aide des �quations horaires, on �tablit que l’�quation cart�sienne de la trajectoire de la balle est :
y = – 4,0.10–3 x 2 + 6,9.10–2 x + 4,9 avec x et y exprim�s en m�tre.
3.3. Le service effectu� est-il r�ussi ?
0= – 4,0.10–3 x 2 + 6,9.10–2 x + 4,9.
x2-17,25x- 1225=0.
Discriminant D =17,252+4 *1225=5197,56 =72,12.
Solution n�gative retenue : x = (17,25-72,1)/2= -27,4.
Cette valeur �tant comprise entre -28 et -16 m, le service est r�ussi.
|
|
