Saut
en parachute, bac S Nlle Calédonie 12 / 2020.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
..
..
|
.
.
|
..
..
......
...
|
1. Etude expérimenntale du saut.
A l'altitude du saut, le pilote met l'avion à l'horizontale, réduit sa
vitesse à 120 km / h. 50 seconde de chute précède l'ouverture du
parachute. Très vite, la vitesse maximale est atteinte, environ 200 km
/ h. Le parachute s'ouvre à 1500 m d'altitude. La descente "sous voile"
dure de 5 à 10 minutes.
Le parachutiste a enregistré lors de son saut, à l'aide de sa montre
connectée, l'altitude z au cours du temps t. L'enregistrement des
données a débuté dès son entrée dans l'avion, sur la piste de
décollage. A son retour, il réalise le graphique suivant en prenant
comme origine des temps le début du saut.
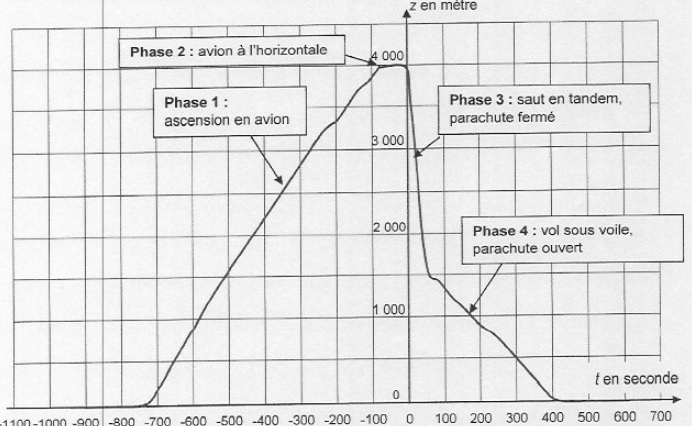
1.1. Justifier l'affectation des équations horaires aux différentes phases.
za(t) = -50 t +4,0 103 ; zb(t) = -4,2 t +1,75 103 ; zc(t) = 6,1 t+4,6 103 ; zd(t) =4,0 103.
t est en seconde, z est en mètre et l'origine z=0 e st prise au niveau du sol.
Phase 1 : l'altitude initiale est nulle ; cette phase débute à t = -750 s d'après le graphe.
zc(-750) =6,1 *(-750) +4,6 103 ~0.
zc(t) = 6,1 t+4,6 103 .
Phase 2 : l'altitude est constante, 4000 m ; zd(t) =4,0 103.
Phase 3 : l'altitude décroît rapidement de 4000 à 1500 m en 50 s d'après le graphe.
za(50) = -50 * 50 +4,0 103 ~1500 m.
za(t) = -50 t +4,0 103 .
Phase 4 : l'altitude décroît jusqu'à zéro, altitude atteinte à t = 410 s d'après le graphe.
zb(410) = -4,2 *410 +1,75 103 ~ 0.
zb(t) = -4,2 t +1,75 103 .
1.2. Montrer que la valeur de la vitesse maximale verticale citée dans l'introduction est compatible avec les données enregistrées.
D'après l'introduction : 200 km / h soit 200 / 3,6 ~55 m / s.
D'après le graphe, lors de la phase 3, la pente du segment de droite est en valeur absolue : (4000-1500) / 50 ~ 50 m/s.
Ces données sont donc compatibles.
2. Etude de la phase 3 du saut.
On
souhaite étudier l'influence de l'altitude z sur la valeur du champ de
pesanteur g. On considère le critère suivant : la valeur g(z) reste
constante si elle diffère de moins de 1 % de sa valeur au niveau du sol.
g(z) = g0(1-2z / RT) si z << RT.
2.1. Peut-on considéré la valeur du champ de pesanteur comme constante et égale à g0 tout au long du saut ? Justifier.
g(z) / g0=1-2z / RT ; 1-g(z) / g0=2z / RT ; (g0-g(z) ) / g0 =2z / RT =8000 / (6,37 106) ~1,3 10-3 ( 0,13 %).
g(z) diffère de moins de 1 % de sa valeur au niveau du sol : g(z) ~g0.
On étudie dans le référentiel terrestre supposé galiléen, le mouvement
du système {tandem} de masse m au cours de sa chute dans le cadre du
modèle de chute libre. Schéma du mouvement juste après le saut.
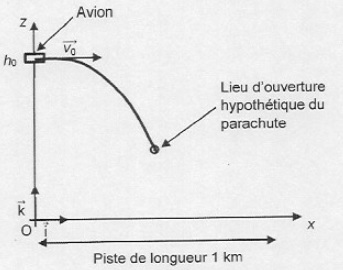
2.2. Montrer que les coordonnées du vecteur accélération du système sont : ax(t) = 0 et ay(t) = -g0.
La chute étant libre, le système n'est soumis qu'à son poids, verticale, vers le bas, valeur mg.
La seconde loi de Newton conduite à : ax(t) = 0 et ay(t) = -g0.
2.3. Etablir que les équations horaires du mouvement du système s'écrivent :
x(t) = v0t; z(t) = -½g0t2+h0.
Le vecteur vitesse est une primitive du vecteur accélération ; de plus
la vitesse initiale est horizontale, de valeur v0.
vx(t) = v0 ; vz(t) = -g0t.
Le vecteur position est une primitive du vecteur vitesse ; de plus la position initiale est : (0 ; h0).
x(t) = v0t; z(t) = -½g0t2+h0.
2.4. En déduire que l'équation de la trajectoire s'écrit : z(x) = -g0x2 / (2v02) +h0.
t = x / v0 ; repport dans z(t), d'où : z(x) = -g0x2 / (2v02) +h0.
2.5. Le tandem ouvre son parachute à l'altitude z = 1500 m. Montrer que cette ouverture s'effectue au dessus de la piste.
v0 = 33 m/s ; h0 = 4000 m.
1500 = -9,8 x2 /(2 * 332) +4000 ; x2 =2500 x 2 *332 / 9,8 =5,56 105 ; x ~7,5 102 m.
Cette valeur étant inférieure à 1 km, l'ouverture s'effectue au dessus de la piste.
2.6. Calculer la durée de la phase 3 et la comparer à celle déduite du graphique. Conclure.
x(t) = v0 t ; t = 7,5 102 / 33 ~23 s.
Le graphe indique une durée voisine de 50 s, soit le double.
Le modèle de la chute libre n'est pas valide.
|
...
|
....
|
3. Etude de la phase 4.
Lors
de la descente parachute ouvert, le moniteur guide le parachute de
manière à maintenir une trajectoire verticale. La force Ff , verticale, vers le haut, modélise l'action de l'air sur le système {tandem}.:
3.1. Associer chacun des schéma à un instant de la chute :
- juste après l'ouverture ;
- quelques secondes avant l'ouverture.
Justifier à partir des données expérimentales.
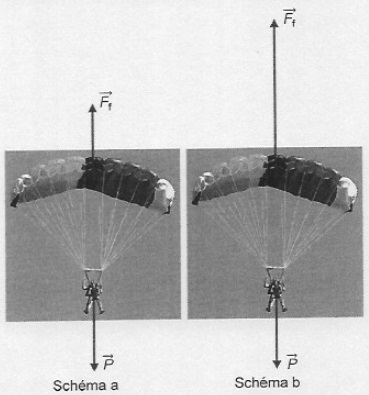
Avant l'ouverture ( schéma a), la vitesse maximale est atteinte, le poids est opposé à la force Ff.
Après l'ouverture, (schéma b), la vitesse diminue, Ff > P.
Quelques secondes après l'ouverture du parachute, la chute du tandem se
fait à vitesse constante. On étudie le mouvement dans ces conditions.
3.2 Estimer la valeur de la vitesse verticale du tandem à partir des données expérimentales.
Phase 4, coefficient directeur ( en valeur absolue) du segment de droite : 1500 / (410-50) ~4,2 m /s ( 4,2 x 3,6 ~ 15 km / h ).
3.3. Déterminer la valeur de Ff.
La chute étant uniforme, le poids du tandem est opposé à la force qui modélise l'action de l'air.
m = 200 kg , g = 9,8 m s-2 ; Ff =200 x9,8 ~2,0 103 N.
3.4 L'expression de Ff est donnée par Ff = kv2z où k est une constante et vz la vitesse verticale de chute. Montrer que k = 1,1 102 S.I. préciser l'unité de k.
k = Ff / v2z =2,0 103 / 4,22 ~1,1 102 N s2 m-2.
3.5 Calculer l'énergie cinétique du tandem avant l'arrivée au sol.
½m v2z =0,5 x200 x4,22 ~1,8 103 J.
3.6 Le tandem possède un parachute de secours plus petit que le parachute principal. On admet que la valeur de la constante ks de la force de frottement exercée par ce parachute vérifie la relation ks = ½k. Dans le cas où le parachute de secours est utilisé, déterminer la valeur de la vitesse verticale vzs ainsi que celle de l'énergie cinétique du tandem avant l'arrivée au sol. Commenter.
v2zs =Ff / ks =2Ff / k = 4,0 103 / (1,1 102)=36,4 ; vzs ~6,0 m /s.
Energie cinétique du tandem : 0,5 x 200 x36 ~3,6 103 J.
L'arrivée au sol est un peu plus brutale, mais sans casse.
|
|