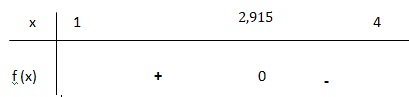Mathématiques,
fonctions exponentielle et logatithme, bac Polynésie 2021.
Convexité, équation différentielle.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
..
..
|
.
.
|
..
..
......
...
|
Fonction exponentielle.
On
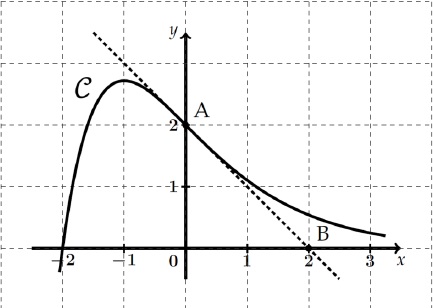
a représenté ci-dessous, dans un repère orthonormé, une portion de la
courbe représentative 𝒞 d’une fonction 𝑓 définie sur 𝐑 :
On considère les points A(0 ;2) et B(2 ;0).
Partie 1.
Sachant que la courbe 𝒞 passe par A et que la droite (AB) est la
tangente à la courbe 𝒞 au point A, donner par lecture graphique :
1. La valeur de f(0) et celle de f ′(0).
f(0) = 2.
f '(0) = coefficient directeur de la tangente en x =0 soit -1.
2. Un intervalle sur lequel la fonction 𝑓 semble convexe.
Intervalle [0 ; +3].
Partie 2.
On note (E) l’équation différentielle y′=−y+e−x.
On admet que g: x↦xe−x est une solution particulière de (E).
1. Donner toutes les solutions sur 𝐑 de l’équation différentielle (H)∶ y′=−y.
y'+y = 0 ; solution générale : y = A e-x avec A une constante.
2. En déduire toutes les solutions sur 𝐑 de l’équation différentielle (E).
Solution générale de (H) + solution particulière de (E) soit :
f(x) = A e-x +xe−x = (A+x)e-x.
3. Sachant que la fonction f est la solution particulière de (E) qui
vérifie f(0)=2, déterminer une expression de f(𝑥) en fonction de x.
(A+0)e-0=2.
A = 2.
f(x) = (2+x)e-x.
Partie 3.
On admet que pour tout nombre réel 𝑥, f(x)=(x+2) e−x.
1. On rappelle que f ′ désigne la fonction dérivée de la fonction f.
a. Montrer que pour tout x∈𝐑, f ′(x)=(−x−1) e−x.
On pose u = x+2 et v = e-x.
u' = 1 ; v' = -e-x.
u'v+v'u = e-x-(x+2)e-x =(−x−1) e−x.
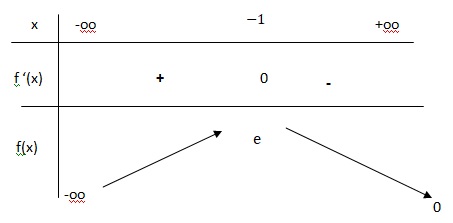
b. Étudier le signe de f ′(x) pour tout x∈𝐑 et dresser le tableau des variations de f sur 𝐑.
On ne précisera ni la limite de 𝑓 en −∞ ni la limite de 𝑓 en +∞.
On calculera la valeur exacte de l’extremum de 𝑓 sur 𝐑.
e-x
f ' a le signe de -1-x.
Si x < -1, f '(x) > 0 et f(x) est strictement croissante.
Si x > -1, f '(x) < 0 et f(x) est strictement décroissante.
Si x = -1, f '(x) =0 et f(x) présente un maximum.
2. On rappelle que f ″ désigne la fonction dérivée seconde de la fonction f .
a. Calculer pour tout x∈𝐑, f ″(𝑥).
On pose u = -x-1 et v = e-x.
u' = -1 ; v' = -e-x.
u'v+v'u = -e-x+(x+1)e-x =x e−x.
b. Peut-on affirmer que f est convexe sur l’intervalle [0 ;+∞[ ?
f " est poositive sur [0 ;+∞[ : f est convexe sur cet intervale.
|
...
|
....
|
Logarithme népérien.
Cet exercice est composé de deux parties.
Certains résultats de la première partie seront utilisés dans la deuxième.
Partie 1 : Étude d’une fonction auxiliaire.
Soit la fonction f définie sur l’intervalle [1 ;4] par : f(x)=−30x+50+35ln(x).
1. On rappelle que f ′ désigne la fonction dérivée de la fonction f.
a. Pour tout nombre réel x de l’intervalle [1 ;4], montrer que :
f ′(x)=(35−30x)/x .
f '(x) = -30 +35 /x = (-30x +35) / x.
b. Dresser le tableau de signe de f ′(𝑥) sur l’intervalle [1 ;4].
f ' a le signe de -30x+35.
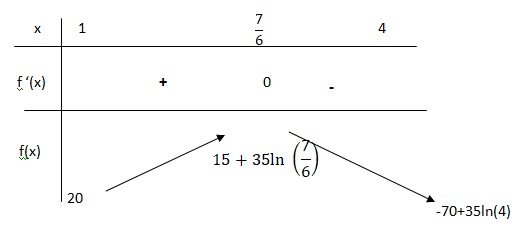
c. En déduire les variations de f sur ce même intervalle.
2. Justifier que l’équation f(x)=0 admet une unique solution, notée a, sur l’intervalle [1 ;4] puis donner une valeur approchée de a à
10−3 près.
Sur [1 ; 7 /6], f(x) > 20 : f(x)=0 ne possède pas de solution sur cet intervalle.
Sur [7 /6 ; 4] f(x) est continue ( car dérivable) et décroissante.
de plus f(7 /6 ) ~20,4 et f(4) ~-21,5.
D'après le théorème de la bijection, f(x) = 0 admet une solution unique sur [7 /6 ; 4].
a ~2,915 d'après la calculatrice.
3. Dresser le tableau de signe de f(x) pour x∈[1 ;4].
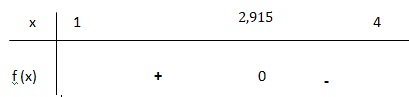
Partie 2 : Optimisation
Une entreprise vend du jus de fruits. Pour x milliers de litres
vendus, avec x nombre réel de l’intervalle [1 ;4], l’analyse des
ventes conduit à modéliser le bénéfice B(x) par l’expression donnée
en milliers d’euros par :
B(x)=−15x2+15x+35x ln x.
1. D’après le modèle, calculer le bénéfice réalisé par l’entreprise
lorsqu’elle vend 2 500 litres de jus de fruits. On donnera une valeur
approchée à l’euro près de ce bénéfice.
B(2,5) = -15 *2,52 +15 *2,5 +35*2,5 ln(2,5) ~-93,75+37,5 +80,17 ~23,925 milliers d'euros.
2. Pour tout x de l’intervalle [1 ;4], montrer que B′(x)=f(x) où B′ désigne la fonction dérivée de B.
B'(x) = -15*2x +15 +35(ln (x)+1)= -30 x+50+35 ln(x) = f(x).
3.a. À l’aide des résultats de la partie 1, donner les variations de la fonction B sur l’intervalle [1 ;4].
B est strictement croissante sur [1 ; a[ et strictement décroissante sur ]a ; 4].
b. En déduire la quantité de jus de fruits, au litre près, que l’entreprise doit vendre afin de réaliser un bénéfice maximal.
B est maximum pour x = a soit environ 2915 litres.
|
|