Mathématiques,
bac S polynésie 2020.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
..
..
|
.
.
|
..
..
......
...
|
Exercice 1. ( 5 points ).
Une urne contient 5 boules rouges et 3 boules blanches indiscernables
au toucher. On extrait une boule de l'urne et on note sa couleur. On
répète 4 fois l'expérience, de manière indépendante, en remettant la
boule à chaque fois dans l'urne. La probabilité d'obtnir au moins une
boule blanche est :
0,15 ; 0,63 ; 0,5 ; 0,85. Vrai.
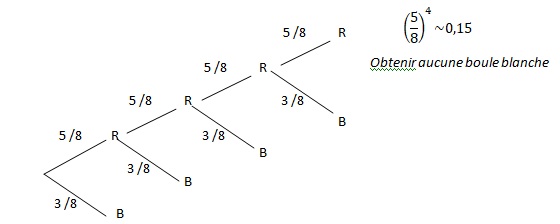
P( obtenir au moins une blanche) = 1 -P( obtenir aucune boule blanche) = 1 - P( obtenir une rouge à chaque tirage)
Il y a 5 boules rouges sur un total de 8.
P( tirer une rouge) = 5 /8.
P( obtenir au moins une blanche) = 1-(5/8)4 ~0,85.
ou bien : soit X la variable aléatoire qui donne le nombre de boule
blanche. X suit une loi binomiale de paramètre n = 4 et p = 3 /8.
P(X > 1) = 1 -P(X=0)=1-(5/8)4 ~0,85.
2. Soitn
un entier naturel supérieur ou égal à 2. Un sac contient n pièces
indiscernables au toucher. Ces pièces comportent toutes un côté " PILE"
et un côté "FACE" sauf une qui contient deux côtés "FACE".
On choisit au hasard une pièce et on la lance. La probabilité d'obtenir le côté "FACE" est :
(n-1) / n ; (n+1) / (2n) , vrai ; 0,5 ; (n-1) / (2n).
Nombre de cas favorables : n+1.
Nombre de cas possibles : 2 n.
Probabilité d'obtenir le côté "FACE" : (n+1) / (2n).
3. On considère T la variable aléatoire suivant le loi normale d'espérance µ =60 et d'écart type s = 6. P(T > 60) (T >72) est :
0,954 ; 1 ; 0,023 ; 0,046. Vrai.
P(T > 60) (T >72)= P((T > 60) n P(T>72)) / P(T > 60) =P(T>72) / P(T > 60) =0,02275 / 0,5 ~0,046.
4.
La durée de fonctionnement ( en années) d'un moteur jusqu'à ce que
survienne la première panne est modèlisée par une variable aléatoire
suivant une loi exponentielle de paramètre l, réel positif.
La probabilité que le moteur fonctionne sans panne plus de trois ans est :
e-3l , vrai ; 1- e-3l ; e-3l ; -1 ; e3l .
D'après le cours :P(X > t) =e-3l.
5. On note X une variable aléatoire suivant la loi uniforme sur [0 ; p /2]. La probabilité qu'une valeur prise par la variable aléatoire soit solution de l'inéquation cos x > 0,5 est égale à :
2 /3 vrai ; 1 /3 ; 1 /2 ; 1 /p.
cos x > 0,5 ; x appartient à :] 0 ; p / 3 ]
Exercice 2. (4 points)
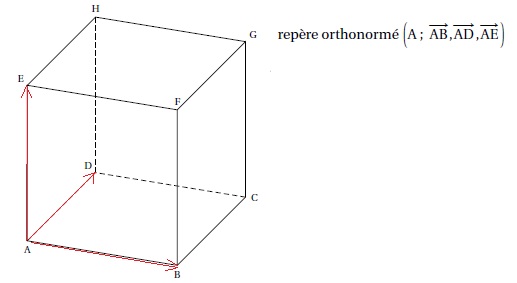
Pour tout réel t, on considère le point M(1-t ; t ; t).
1. Montrer que pour tout réel t, le point M appartient à la droite (BH).
Montrer que trois points M, B et H sont alignés revient à montrer que les deux vecteurs suivants sont colinéaires.
Coordonnées des points : B(1 ; 0 ; 0) ; H (0; 1 ; 1) ; M(1-t ; t ; t)
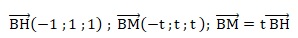
On admet que les droites (BH) et (FC) ont respectivement pour représentation paramétrique :
x=1-t ; y =t ; z = t avec t réel.
x=1 ; y=t' ; z = 1-t' avec t' réel.
2. Montrer que ces droites sont orthogonales et non coplanaires.
Coordonnées du vecteur directeur de la droite (BH) : (-1 ; 1 ; 1).
Coordonnées du vecteur directeur de la droite (FC) : (0 ; 1 ; -1).
Le produit scalaire de ces deux vecteurs directeurs [ 0*(-1) +1*1+1*(-1)) =0) étant nul, ces deux droites sont perpendiculaires.
Si deux droites perpendiculaires sont sécantes alors elles se coupent en un point de coordonnées (x ; y ; z) telles que :
1-t = 1 soit t = 0 ; t = t' =0 ; t = 1-t' est impossible..
Donc les deux droites ne sont pas coplanaires.
3. Pour tout réel t', on considère le point M' (1 ; t' ; 1-t').
a. Montrer que pour tous réels t et t' : MM'2 = 3(t-1 /3)2 +2(t'-0,5)2 +1 /6.
Coordonnées du vecteur MM' : [1-(1-t) ; t'-t ; 1-t'-t].
MM'2 = t2+(t'-t)2+(1-t'-t)2.
MM'2 = t2+t'2+t2-2tt' +1+t'2+t2+2tt'-2t-2t'.
MM'2 =3t2+2t'2-2t'-2t +1.
MM'2 =3t2+1/3-2t +2t'2-2t'+1/2 +1/6.
MM'2 =3(t2+1/9-2t/3) +2(t'2-t'+1/4)+1/6.
MM'2 = 3(t-1 /3)2 +2(t'-0,5)2 +1 /6.
b. Pour quelles valeurs de t et t' la distance MM' est-elle minimale ? Justifier.
MM'2 est la somme de trois termes positifs.
MM'2 est minimale lorsque les deux premiers termes sont nuls soit t = 1 /3 et t' = 0,5.
4. On nomme P le point de coordonnées (2 /3 ; 2 /3 ; 1 /3) et Q le point de coordonnées (1 ; 0,5 ; 0,5).
Justifier que la droite (PQ) est perpendiculaires aux deux droites (BH) et (FC).
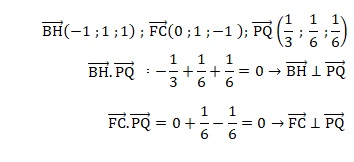
|
...
|
....
|
Exercice 3. ( 6 points).
On considère la fonction f définie sur R par f(x) =x exp(-x2+1). On note C sa courbe représentative dans un repère orthonormé.
1. a Montrer que pour tout réel f(x) = e / x * x2 /exp(x2).
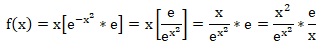
b. En déduire la limite de f(x) quand x tend vers plus l'infini.
Quand x tend vers plus l'infini :
1 /x tend vers zéro ; e / x tend donc vers zéro.
ex / x tend vers plus l'infini et en conséquence x / ex tend vers zéro.
On pose X = x2 ;
eX / X tend vers plus l'infini et en conséquence X / eX tend vers zéro.
Par produit des limites, la limite de f(x) quand x tend vers plus l'infini est égale à zéro.
2. Pour tout réel x, on considère les points M et N de la courbe C d'abscisses respectives x et -x.
a. Montrer que le point O est le milieu du segment [MN].
Coordonnées du milieu du segment [MN] :
(xM + xN) / 2 = (x-x) / 2 = 0.
(yM + yN) / 2 =[ x exp(-x2+1)-x exp(-x2+1)] / 2 = 0.
b. Que peut-on en déduire pour la courbe C ?
La courbe C est symétrique par rapport au point O.
3. Etudier les variations de f sur l'intervalle [0 ; +oo[.
On pose u = x et v = exp(-x2+1) ; u' = 1 ; v' = -2x exp(-x2+1).
u'v+v'u = exp(-x2+1) -2x2 exp(-x2+1).
f '(x) = (1-2x2)exp(-x2+1).
exp(-x2+1). est toujours positif.
1-2x2= 0 si x =1 /2½. f(x) admet un maximum de valeur 1 /2½ exp(0,5)~1,16.
1-2x2> 0 si 0 < x <1 /2½ et f(x) est strictement croissante.
1-2x2 < 0 si 1 /2½ < x et f(x) est strictement décroissante.
4.a Montrer que l'équation f(x) = 0,5 admet sur [0 ; +oo[ exactement deux solutions notées a et ß. ( a < ß).
Le maximum de la fonction f(x) est supérieur à 0,5.
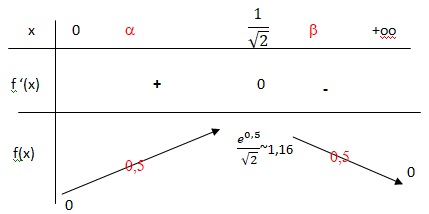
b. En déduire les solutions sur [0 ; +oo[ de l'inéquation f(x) > 0,5.
D'après le tableau de variations, les solutions appartiennent à [a ; ß].
c. Donner une valeur approchée à 10-2 près de a et ß.
La calculatrice donne a ~0,19 et ß ~1,43.
5. Soit A un réel strictement positif. On pose 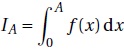
a. Justifier que IA = 0,5(e-exp(-A2+1)).
Soit F une primitive de f(x). IA = F(A)-F(0).
La primitive de la fonction u' exp(u) est F =exp(u).
Si u = -x2+1, alors u' = -2x.
F = -0,5 exp(-x2+1).
IA = F(A)-F(0) = -0,5 exp(-A2+1)+0,5e =0,5(e-exp(-A2+1)).
b. Calculer la limite de IA en + oo.
En plus l'infini : exp(-A2+1) = 0 ; la limite de IA en +oo est donc 0,5e.
On admet que cette limite est l'aire en unités d'aire située entre la courbe C sur [0 ; +oo[ et l'axe des abscisses.
6. On s'intéresse à la partie grisée du plan limitée par :
La courbe C sur R et la courbe C' symétrique de C par rapport à l'axe des abscisses ;
le cercle de centre W ( 1 /2½ ; 0) et de rayon 0,5 et son symétrique par rapport à l'axe des ordonnées.
On admet que le disque de centre W et de rayon 0,5 et son symétrique par rapport à l'axe des ordonnées sont situés entièrement entre la courbe C et la courbe C'.
Déterminer une valeur approchée en unité d'aire au centième près de l'aire de cette partie grisée du plan.
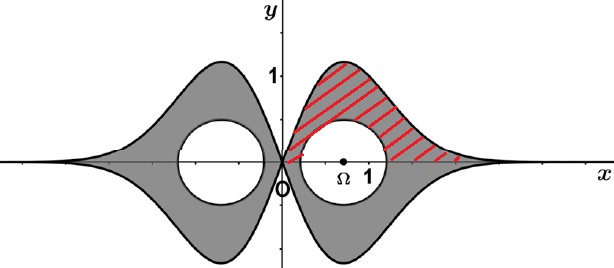
L'aire cherchée est égale à 4 fois l'aire hachurée.
Aire du demi disque de rayon 0,5 : pR2/2 = 3,14 x0,52 /2~0,3927.
Aire cherchée = 4(0,5 e-0,3927) ~3,87 unités d'aire.
Exercice 4. ( 5 points).
Le plan complexe est muni d'un repère orthonormé direct.
On considère la suite de nombres complexes (zn) définie par :
z0 =0 et pour tout entier n, zn+1=(1+i)zn-i.
On note An le point d'affixe zn. On note B le point d'affixe 1.
1.a. Montrer que z1 = -i et que z2 = 1-2i.
z1=(1+i)z0-i = -i.
z2=(1+i)z1-i = =-(1+i)i-i =-2i-i2=1-2i.
b. Calculer z3.
z3=(1+i)z2-i = =(1+i)(1-2i)-i =1-2i+i-2i2-i= 3-2i.
c. Placer les points B, A1, A2 et A3.
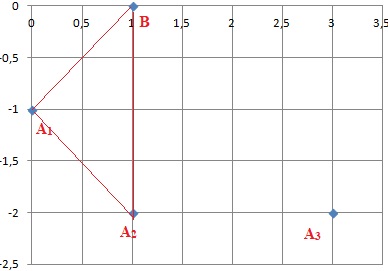
d. Démontrer que le triangle BA1A2 est rectangle isocèle.
A1B2=12+12=2.
A1A22=12+(-2-(-1))2=2.
A1B=A1A2 : le triangle BA1A2 est isocèle.
A2B2=(1-1)2+(-2-0)2=22= A1B2 +A1A22.
D'après la réciproque du théorème de Pythagore, le triangle BA1A2 est rectangle est A1.
2. Pour tout entier naturel n, on pose un = |zn-1|.
a. Démontrer que un+1 = 2½un.
|zn+1-1|=|(1+i)zn-i-1|= |(1+i)zn-(i+1)|=|(1+i) (zn-1)|.
|zn+1-1|=(12+12)½ |zn-1| =2½|zn-1| ; un+1 = 2½un.
b. Déterminer à partir de quel entier naturel n, la distance BAn est strictement supérieure à 1000.
BAn =|zn-1| =un.
La suite (un) est géométrique de raison 2½ et de premier terme u0 =|0-1| =1.
un = (2½)n > 1000 ; n ln(2½) > 1000 ; 0,5n ln(2) > ln(1000 );
n > 2 ln(1000) / ln(2) ; n >20.
3. a. Déterminer la forme exponentielle du nombre complexe z=1+i.
Module de z : |z| = (12+12)½ = 2 ½.
z / |z| = 1 / 2 ½+ i/ 2 ½ = cos (p/4) + i sin (p /4).
z = 2½exp(ip/4).
b. Démontrer par récurence que pour tout entier naturel zn = 1-20,5n exp(i n p/4).
Initialisation : z0 = 0= 1-20 exp(0)1-1=0.
La propriété est vraie au rang zéro.
Hérédité : la propriété est supposée vraie au rang n.
zn = 1-20,5n exp(i n p/4).
zn+1=(1+i)zn-i.
1+i =2½exp(ip/4) ;
zn+1=2½exp(ip/4) [1-20,5n exp(i n p/4)] -i.
zn+1=2½exp(ip/4) -20,5(n+1) exp(i (n+1) p/4)] -i.
zn+1=1+i -20,5(n+1) exp(i (n+1) p/4)] -i.
zn+1=1 -20,5(n+1) exp(i (n+1) p/4)].
La propriété est vraie au rang n+1.
Conclusion : la propriété est vraie au rang zéro et héréditaire ; elle est vraie pour tout entier n.
c. Le point A2020 appartient-il à l'axe des abscisses ? Justifier.
z2020 = 1-21010 exp(i 505 p).
505 p = 252 x 2p+p.
z2020 = 1-21010 exp(i p) = 1+21010, nombre réel.
Le point A2020 appartient à l'axe des abscisses.
|
|