Mathématiques,
bac ST2S Antilles 2020.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
..
..
|
.
.
|
..
..
......
...
|
Exercice 1. ( 5 points ).
Un groupe hospitalier possède deux maisons de retraite nommées
"Mésange" et "Rossignol". Ces deux maisons comptent 120 résidents
au total dont 80 à la résidence "Mésange". Les soignants de ce groupe
hospitalier évaluent la capacité des résidents à s'habiller en
autonomie suivant une grille à trois niveaux A, B et C.
45 résidents de la maison "Mésange" sont évalués au niveau A.
50 % des résidents de la maison "Rossignol" sont évalués au niveau B.
20 résidents au total sont évalués au niveau C, dont la moitié à la maison "Mésange".
On choisit au hasard un des résidents de ces maisons et on considère les événements suivants :
M : " la personne est un résident de la maison Mésange".
A : " la personne est évaluée au niveau A".
B : " la personne est évaluée au niveau B".
C : " la personne est évaluée au niveau C".
1. Compléter le tableau suivant.
|
A
|
B
|
C
|
Total
|
Résidents " Mésange"
|
45
|
25
|
10
|
80
|
Résidents " Rossignol"
|
10
|
20
|
10
|
40
|
Total
|
55
|
45
|
20
|
120
|
2.a. Déterminer la probabilité de l'événement M et la probabilité de l'événement C.
P(M) =80 / 120 = 2 / 3 ~0,667.
P(C) = 20 / 120 = 1 / 6 ~0,167.
2.b. Décrire par une phrase l'événement M n A et calculer sa probabilité.
Le résident habite la résidence "Mésange" et est évalué au niveau A.
P(M n A) = 45 / 120 = 3 / 8 =0,375.
2.c. Calculer la
probabilité que la personne choisie au hasard réside dans la maison
"Mésange" sachant qu'elle est évaluée au niveau A.
PA(M) =45 / 55 =9 / 11 ~0,818.
2.d. Calculer la probabilité P non M (C) et interpréter cette probabilité dans le contexte de l'exercice.
P non M (C)= 10 / 120 = 1 / 12 ~0,083.
La probabilité que le résident habite la résidence "Rossignol" et soit classé au niveau C est égale à 0,083.
Exercice 2. 8 points.
Partie A.
Le tableau ci-dessous présente l'évolution, en milliers, du nombre de
femmes médecins généralistes en France entre les années 2013 et
2018.
Année
|
2013
|
2014
|
2015
|
2016
|
2017
|
2018
|
Rang de l'année xi
|
0
|
1
|
2
|
3
|
4
|
5
|
Nombre de femmes médecins généralistes ( en milliers)
|
42,4
|
43,5
|
44,6
|
45,4
|
46,4
|
47,7
|
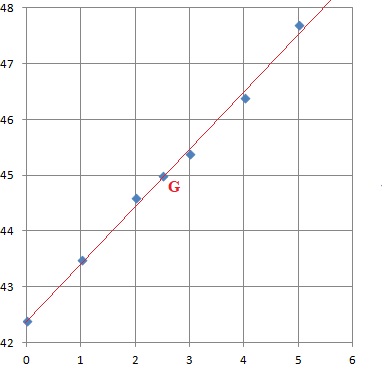
On donne le nuage de points Mi(xi, yi).
1. Déterminer les coordonnées (xG, yG) du point moyen G de ce nuage. Placer ce point sur le graphique.
xG=(0 +1 +2 +3 +4 +5) / 6=15 / 6 =2,5.
yG =(42,4 +43,5+44,6 +45,4 +46,4 +47,7) / 6 =45.
2. D'après la forme du nuage, on peut envisager un ajustement affine. On admet que la droite D d'équation y = 1,03 x +42,4 réalise cet ajustement. Ce modèle est valable jusqu'en 2025.
a. Construire la droite D en précisant les coordonnées des points utilisés.
La droite passe par le point G et par le point de coordonnées ( 0 ; 42,4).
b. Selon ce modèle, estimer le nombre de femmes médecins généralistes en 2021.
x = 8 ; y = 1,03 * 8 +42,4 =50,64 milliers.
Partie B.
Le nombre de médecins généralistes devrait baisser de 0,9 % chaque année de 2018 à 2025.
1.
En 2018, le nombre de médecins généralistes en France est d'environ
102,5 milliers. Si on admet que ce nombre a diminué de 0,9 % entre 2018
et 2019, montrer que le nombre de médecins généralistes en France en
2019 était d'environ 101,6 milliers.
1-0,9 / 100 = 0,991.
0,991 x 102,5 ~101,6 milliers.
2. On note v0=102,5, le nombre de médecins généralistes pour l'année 2018 et vn
l'estimation du nombre de médecins généralistes en milliers, selon ce
modèle, pour l'année 2018 +n, où n est un entier positif ou nul.
a. On veut utiliser la feuille de calcul ci-dessous afin d'obtenir les valeurs successives de la suite (vn).
|
A
|
B
|
1
|
n
|
vn
|
2
|
0
|
102,5
|
3
|
1
|
101,6
|
4
|
2
|
|
5
|
3
|
|
Parmi
les formules suivantes, laquelle a-t-on entrée dans la cellule B3 de
sorte que, recopiée vers le bas, elle permette d'afficher les valeurs
de la suite (vn) ?
= B2*0,009 ; =B$2*0,009 . =B2*0,991 . =B$2*0,991.
b. Indiquer la nature de la suite (vn) et donner sa raison.
Suite géométrique de raison 0,991.
c. Exprimer vn en fonction de n.
vn = v0 x0,991n = 102,5 x0,991n.
d. Déterminer une estimation du nombre de médecins généralistes en France en 2023 selon ce modèle.
n = 5 ; v5 = 102,5 x0,9915 ~97,97 ~98 milliers.
Partie C.
Déterminer, selon les modèles d'évolution pproposés dans les parties A
et B, à partir de quelle année on peut estimer qu'il n'y aura
plus de médecins généralistes femmes que de médecins généralistes
hommes parmi les médecins généralistes.
Médecins généralistes femmes : 1,03 n +42,4.
Médecins généralistes hommes et femmes :102,5 x 0,991n.
Médecins généralistes hommes : 102,5 x 0,991n-1,03 n +42,4.
année
|
2018
|
2019
|
2020
|
2021
|
Hommes
|
54,8
|
53,0
|
51,05
|
49,11
|
Femmes
|
47,7
|
48,58
|
49,61
|
50,64
|
.
|
...
|
....
|
Exercice 3. ( 7 points).
On s'intéresse au taux de glycémie après un repas d'un patient.
Partie A.
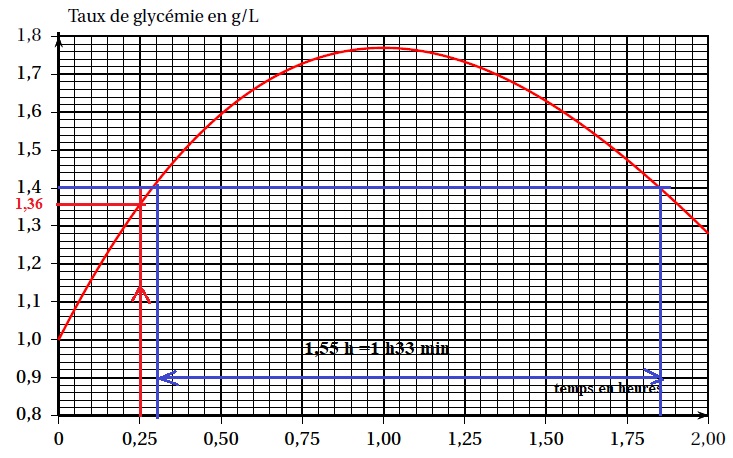
Le graphique suivant repprésente le taux de glycémie de ce patient,
exprimé en g / L, en fonction du temps écoulé depuis son repas, exprimé
en heures. Répondre aux questions suivantes par lecture graphique.
1. Déterminer le taux de glycémie en g / L un quart d'heure après le repas.
2.a. Déterminer à quels moments le taux de glycémie a été égal à 1,4 g / L.
b. Chez une personne en bonne santé, la glycémie après un repas doit rester inférieure à 1,4 g / L.
Estimer la durée en minutes pendant laquelle le taux de glycémie de ce patient a dépassé cette valeur.
Partie B.
Chez ce patient, l'évolution du taux de glycémie ( en g / L) en
fonction du temps t ( en heure) peut être modélisée par la fonction f
définie sur l'intervalle [0 ; 2 ] par :
f(t) = 0,14 t3-1,05t2 +1,68 t +1.
1. Déterminer f '(t).
f '(t) = 0,14 *3 t2 -1,05 *2t +1,68 =0,42 t2 -2,1 t +1,68.
2. Vérifier que f '(t) = 0,42 (t-1)(t-4).
0,42 (t-1)(t-4) = 0,42 (t2-4t-t+4) =0,42 t2 -2,1 t +1,68.
3. Compléter le tableau suivant.
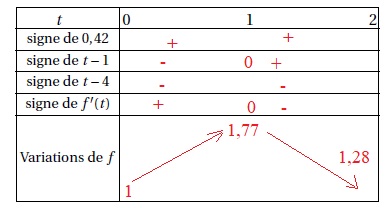
4. En déduire la valeur maximale, selon ce modèle, du taux de glycémie de ce patient.
|
|