Mathématiques,
bac ST2S Métropole, La Réunion 2020.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
..
..
|
.
.
|
..
..
......
...
|
Exercice 1.
( 5 points ).
Sur une feuille de calcul, le tableau suivant donne le nombre de licences prises à la FFH de 2008 à 2012.
|
A
|
B
|
C
|
D
|
E
|
F
|
1
|
Année
|
2008
|
2009
|
2010
|
2011
|
2012
|
2
|
Nombre de licences
|
24 456
|
25 775 |
26 534
|
27 657
|
31 900
|
3
|
Taux d'évolution entre deux années consécutives (%)
|
X
|
5,4
|
|
|
|
1. Calculer le taux d'évolution de licences de 2008 à 2012.
(31 900-24 456) / 24 456 x 100 ~30,4 %.
2.
La ligne 3 est au format pourcentage. Quelle formule doit-on saisir en
C3 pour obtenir, par recopie vers la droite, les taux d'évolution entre
deux années consécutives ?
=(C2-B2)/B2
Suite
à une nouvelle offre sportive attractive, on considère qu'à partir de
2012, le nombre de licences augmente chaque année de 6 %. Avec ce
modèle, on note un le nombre de licences, en milliers, l'année 2012 +n. On a donc u0 = 31,9.
3.a. Donner la nature de cette suite en précisant sa raison.
Suite géométrique de raison 1,06.
3.b. Exprimer un en fonction de n.
un = u0 x1,06n = 31,9 x 1,06n.
3.c Calculer u4 et interpréter.
u4 = 31,9 x 1,064 ~40,3.
En 2016, il y a environ 40300 licences.
4.a Montrer qu'avec ce modèle l'objectif "Cap 2024" ( 75 000 licences) ne serait pas atteint.
u12 = 31,9 x 1,0612 ~64,2, valeur inférieure à 75.
4.b. Déterminer en quelle années le nombre de licences dépasserait 75 000.
un = 31,9 x1,06n > 75 ; 1,06n > 75 / 31,9 ; 1,06n > 2,35 ; n ln(1,06 ) > ln(2,35) ; n > 14,67 soit 15 ( année 2027).
u14= 31,9 x 1,0614 ~72,1 ; u15= 31,9 x 1,0615 ~76,5.
Exercice 2. 8 points.
Partie A.
Le
tableau ci-dessous donne le taux moyen d'abandon scolaire des jeunes
âgés de 18 à 24 ans dans l'Union Européenne de 2006 à 2013.
Année
|
2006
|
2007
|
2008
|
2009
|
2010
|
2011
| 2012
|
2013
|
Rang
de l'année xi
|
0
|
1
|
2
|
3
|
4
|
5
| 6
|
7
|
taux moyen d'abandon scolaire yi ( %)
|
15,3
|
14,9
|
14,7
|
14,2
|
13,9
|
13,4
| 12,7
|
11,9
|
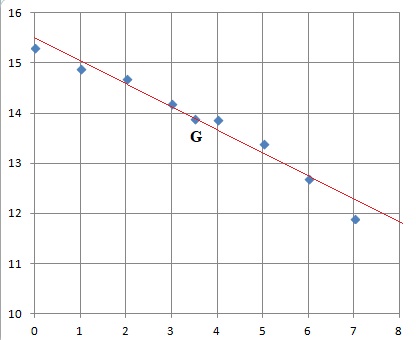
On donne le nuage de
points Mi(xi, yi).
1. Déterminer les
coordonnées (xG, yG) du point moyen G de ce
nuage. Placer ce point sur le graphique.
xG=(0 +1 +2 +3 +4 +5+6+7) / 8=15 / 6 =3,5.
yG =(15,3 +14,9+14,7 +14,2 +13,9 +13,4+12,7+11,9) / 8 =13,88.
2. D'après la forme du nuage, on
peut envisager un ajustement affine. On admet que la droite D d'équation y = -0,45
x +15,5 réalise cet ajustement.
Construire la
droite D en
précisant les coordonnées des points utilisés.
La droite passe par le point G et par le point de coordonnées ( 0 ; 15,5).
3. Selon ce modèle, estimer le
nombre de taux moyen d'abandons en 2017.
x = 11 ; y = -0,45*11 +15,5 =10,55 %.
4. Déterminer au cours de quelle année le taux moyen d'abandon passera en dessous de 9 %.
-0,45 x+15,5 < 9 ; 0,45 x > 15,5-9 ; x > 6,5 / 0,45 ; x > 14,4.
Au cours de l'année 2019, ce taux passera en dessous de 9 %.
Partie B.
Le tableau suivant donne les résultats d'une enquète concernant un
échantillon de jeunes de 18 à 25 ans selon la catégorie professionnelle
du père.
|
Jeunes sortis sans diplôme
|
Jeunes sortis avec diplôme
|
Total
|
Père ouvrier
|
40
|
140
|
180
|
Père non ouvrier ( employés )
|
40
|
280
|
320
|
Total
|
80
|
420
|
500
|
En
utilisant les données de ce tableau, pour chacune des affirmations
suivantes, indiquer si elle est vraie ou fausse en justifiant par un
calcul.
1. Parmi les jeunes sortis sans diplôme, près de la moitié ont un père ouvrier. Vrai.
40 / 80 = 0,5.
2. Près de 85 % des enfants d'employés sortent avec un diplôme. Faux.
280 / 320 =0,875.
Partie C.
On considère un échantillon de jeunes de 18 à 25 ans selon la catégorie
socio-professionnelle du père. On choisit au hasard la fiche d'un jeune
dans cette population et on considère les événements suivants :
D : le jeune est sorti avec diplôme.
O : le jeune a un père ouvrier.
84 % des jeunes interrogés sont sortis avec un diplôme, et parmi ces 84 %, 32 % ont un père ouvrier.
Parmi les jeunes sortis sans diplôme, la moitié ont un père ouvrier.
1. Compléter l'arbre de probabilités suivant.
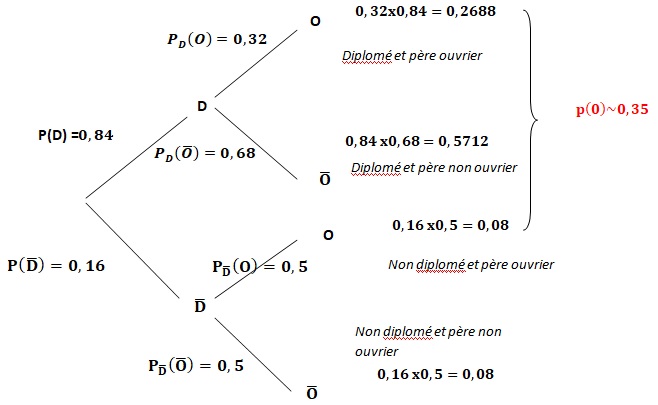
2. Préciser Pnon D (O) et interpréter.
Pnon D (O)=0,08.
La probabilité d'être non diplomé en ayant un père ouvrier est égale à 0,08.
3. Interpréter l'événement D n O et calculer sa probabilité.
Le jeune diplomé a un père ouvrier. Sa probabilité est égale à 0,32 x0,84 = 0,2688.
4. a. Montrer que P(O) ~0,35.
Formule des probabilités totales : 0,32 x 0,84 + 0,16 x0,5 ~0,35.
4.b. Les événements O et D sont-ils indépendants ? Justifier.
P(O) = 0,35 ; P(D) = 0,84 ; P(O) xP(D) =0,35 x0,84 =0,294.
P(O n D) =0,2688, différe de 0,294.
Les événements O et D ne sont pas indépendants.
|
...
|
....
|
Exercice 3.
( 7 points).
Un
médecin donne une dose de médicament à 2 patients en utilisant deux
voies d'administration différentes : par voie orale ou par voie
intraveineuse.
Partie A.
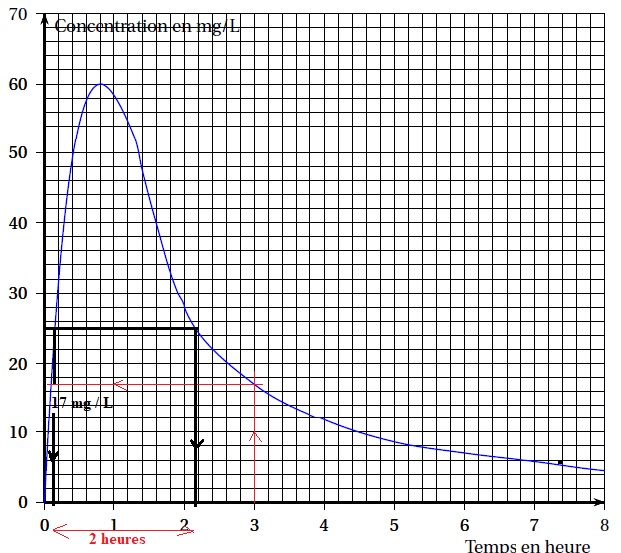
Une dose de 60 mg / L de ce médicament est administrée par voie oral au
premier patient à l'instant t =0. La courbe suivante représente la
concentration en mg / L du médicament dans le sang du patient en
fonction du temps par heure. Répondre aux questions suivantes en
utilisant le graphe.
1. Déterminer la concentration du médicament à t = 3 heures. 17 mg / L
2. Au bout de combien de temps la concentration est-elle maximale ? 0,8 h ou 48 minutes.
3. Déterminer la durée pendant laquelle la concentration du médicament reste à l'intérieur de l'intervalle thérapeutique ( C > 25 mg / L).
Environ 2 heures.
Partie B.
Le second patient reçoit une dose de 60 mg / L de ce médicament par
voie intraveineuse. On admet que la concentration ( en mg / L) du
médicament dans le sang du patient, en fonction du temps écoulé ( en
heure) depuis l'injection, est donnée par la fonction g définie sur
l'intervalle [0 ; 7] par : g(t) = 60 x 0,75t.
1. Déterminer le sens de variation de la fonction f(t) = 0,75t.
0 < 0,75 < 1 donc 0,75t est décroissante sur [0 ; 7].
2. a. Compléter le tableau suivant :
t
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
g(t)
|
60
|
45
|
33,8
|
25,3
|
19,0
|
14,2
|
10,7
|
8,0
|
2.b. Compléter la courbe représentative de la fonction g.
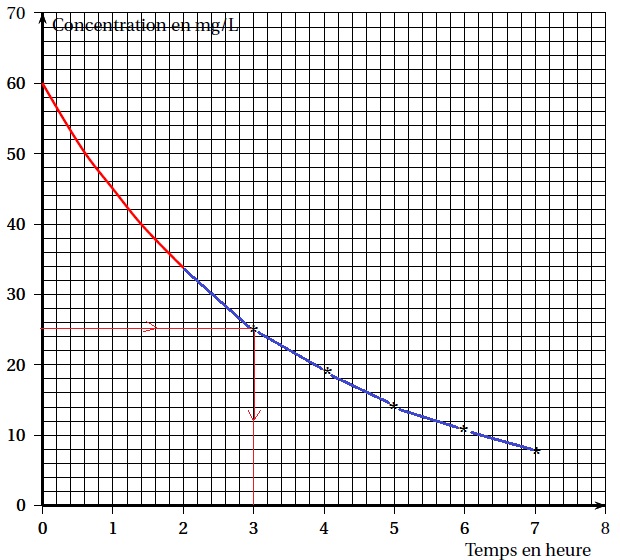
3. Résoudre dans l'intervalle [0 ; 7 ] l'inéquation g(t) < 25.
60 x 0,75t < 25 ; 0,75t < 25 /60 ; 0,75t < 0,417 ;
t ln(0,75) < ln(0,417) ; -0,288 t < -0,875 ; t > 0,875 / 0,288 ; t > 3 heures.
Partie C.
Déterminer le mode d'administration à privilégier pour que la durée d'efficacité du médicament soit la plus longue.
Par voie orale, l'intervalle thérapeutique est de 2 heures.
Par voie intraveineuse, l'intervalle thérapeutique est de 3 heures. Ce mode d'administration est à privilégier.
|
|