Mathématiques, bac Sti2d
2021.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
..
..
|
|
Le candidat choisit 4 questions parmi les 6 proposées.
Question 1.
On considère le nombre complexe z= (2-6i) / (2-i). Déterminer sa forme algébrique.
Multiplier numérateur et dénominateur par 2+i.
z = (2-6i)(2+i) / [(2-i)(2+i)] = (4+2i-12i-6i2) / (4-i2) =(10-10i)/ 5 =2-2i.
Question 2. On considère le nombre complexe z = -2-2i.
a. Déterminer sa forme exponentielle.
Module de z : |z| =[(-2)2+(-2)2]½ =(4+4)½ =8½ = 2 . 2½.
z / |z| =-1 /2½ -i / 2½ = cos ( 5 p/4) + i sin(5 p/4)
z = 2 . 2½ exp (i 5 p/4).
b. Montrer que z4 est un nombre réel à déterminer.
z4 =(2 . 2½)4 exp (i 5 p / 4 x 4) =64 exp(i 5 p).
5 p = 2 x(2p) + p ; exp(i 5 p) = exp(i p) = -1
z4 =64 exp(i p) = - 64.
Question 3.
On considère A, B, C les points du plan d'affixes respectives :
zA = 2-2i ; zB = -2-2i ; zC = -4i.
a. Placer ces points dans le plan complexe.
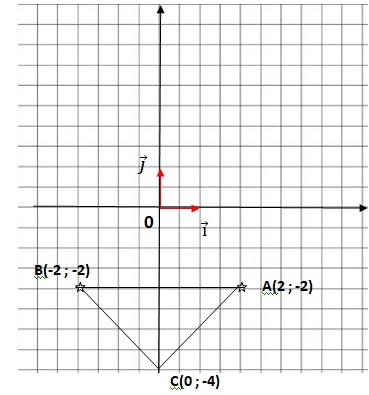
b. Montrer que le triangle ABC est rectangle et isocèle.
BC2=[(0-(-2))2+(-4-(-2))2]=(4+4=8 ; BC = 2 . 2½.
AC2=[(0-(-2))2+(-4-(-2))2]=(4+4=8 ; AC = 2 . 2½.
Le triangle ABC est isocèle.
AB2=[(-2-2)2+(-2-(-2))2]=16.
AB2=BC2 +AC2.
D'après la réciproque du théorème de Pythagore, le traingle ABC est rectangle en C.
Question 4.
On considère l'équation différentielle y' +5y = 7 où y est une fonction de la variable t, définie et dérivable sur R.
a. Résoudre cette équation.
Solution générale de y' + 5y =0 : y = k e-5t avec k une constante.
Solution particulière de y' +5y=7 : y = 7 /5 = 1,4.
Solution générale de y' +5y = 7 : y = k e-5t +1,4.
b. Préciser l'expression de la solution f vérifiant f(0)=4.
f(0) = 4 = k e0 +1,4 = k +1,4 ; k = 2,6.
f(t) = 2,6 e-5t +1,4.
Question 5.
Soit g la fonction définie et dérivable sur ]0 ; + oo[ par g(x) =x ln(x) -x+4.
a. Montrer que sa dérivée g '(x) = ln(x).
On pose u = x et v = ln(x) ; u' = 1 ; v' = 1 /x ;
u'v+v'u =ln(x) +x / x = ln(x) +1.
Dérivée de -x+4 : -1.
g'(x) = ln(x)+1-1 = ln(x).
b. En déduire le sens de variation de g.
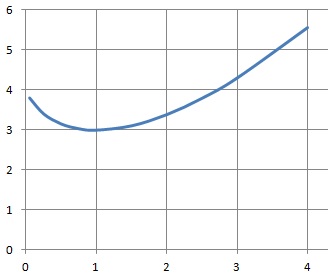
Sur ]0 ; 1[, ln(x) < 0 et g(x) est strictement décroissante.
Sur ]1 ; + oo[, g'(x) est positive et g(x) est strictement croissante.
Si x = 1, g'(x) est nulle et g(x) présente un minimum.
Question 6.
On considère la fonction h définie sur R par h(x) = x2e-x.
a. Calculer la limite en -oo.
x2 tend vers +oo et e-x tend vers +oo ; h(x) tend vers +oo.
b. Calculer la limite en +oo.
x2 tend vers +oo et e-x tend vers zéro ; h(x) tend vers zéro.
On admet que h est strictement décroissante sur [2 ; +oo[ et que
l'équation h(x) = 0,5 addmet une unique solution dans cet intervalle
que l'on note a. Compléter le programme ci-dessous pour que la fonction sol_bal détermine une valeur approchée de a à 10-n près.
def sol_ bal(n) :
x=2
while x2e-x > 0,5 :
x = 2+10-n
return x.
|

