Mathématiques,
bac STI2D biotechnologies Antilles 2020.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
..
..
|
.
.
|
..
..
......
...
|
Exercice
1.
Dans un centre avicole, les oeufs sont pesés suivant 4 catégories avant expédition.
XL : très gros oeufs d'un poids supérieur ou égal à 73 g ;
L : très gros oeufs d'un poids supérieur ou égal à 63 g et strictement inférieur à 73 g ;
M : pour des oeufs moyens d'un poids supérieur ou égal à 53 g et strictement inférieur à 63 g ;
S : pour les petits oeufs dont le poids est strictement inférieur à 53 g.
On note G la variable aléatoire qui prend pour valeur la masse ( en gramme ) d'un oeuf.
On admet que G suit la loi normale de moyenne µ= 60 et d'écart type s.
1. Sachant que P(52,8 < G < 67,2 =0,95, déterminer s.
On pose Z =( G-µ) / s.
P(52,8 -60 < G-60 < 67,2 -60=0,95.
P( -7,2 < G-60 < 7,2) = 0,95.
P( -7,2 / s < Z < 7,2) / s = 0,95.
2P(Z < 7,2 / s)-1 = 0,95 ; P(Z < 0,9 / s) =0,975 ;
s = 3,7.
Pour la suite de l'exercice, on prend s =4.
2. On prélève au hasard un oeuf dans ce centre.
a. Déterminer la probabilité que cet oeuf soit moyen
P (53 < G < 63) ; P (53 < G) =0,00406 ; P (63 < G) =0,7734 ;
P (53 < G < 63) =0,7734 -0,00406 =0,7333.
b. Déterminer la probabilité que cet oeuf soit un très gros oeuf.
P (G > 73)=1- P(73 < G)=1- 0,9994 ~0,0006.
3. Ce centre affirme que le nombre d'oeufs de catégorie L correspond à 37 % du nombre total d'oeufs.
Sur un lot choisi au hasard de 35 douzaines d'oeufs non triés, on
comptabilise 168 oeufs de catégorie L. Avec un risque d'erreur de 5 %,
l'affirmation du centre avicole est-elle remise en cause ?
n = 35 x12=420 ; p = 0,37 ; [ p(1-p) / n ]½= (0,37 x0,63 / 420)½
=0,0236.
1,96 x[ p(1-p) / n ]½=1,96
x0,0236 ~0,0462.
0,37 -0,0462 ~0,324 ; 0,37 +0,0462 ~0,416.
Intervalle de fluctuation asymptotique à 95 % : [0,324 ; 0,416 ].
Fréquence observée 168 / 420 = 0,40.
La fréquence observée appartient à l'intervalle de fluctuation.
On ne peut pas mettre en doute l'affirmation du centre.
Exercice 2.
Une
infection est traitée en injectant un médicament par voie
intraveineuse. A l'instant t=0, on injecte au patient une dose de 3 UI
du médicament qui se diffuse instantanément dans le sang. Le médicament
est progressivement éliminé. La quantité de médicament diminue de 20 %
par heure. Pour conserver son efficacité thérapeutique, on injecte
toute les heures une dose de 2 UI au patient, en évitant un surdosage.
On modélise cette situation à l'aide d'une suite u. On a u0 = 3.
Partie A.
1. Montyrer que u1 = 4,4.
u1 = 0,8 u0 +2 = 0,8 x3 +2 = 4,4.
2.
On réalise une feuille de tableur. Parmi les formules proposées,
reporter sur votre copie celle entrée en B3, qui, recopiée vers le bas,
donne les valeurs successives de un.
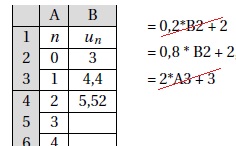
3. La suite u est-elle géométrique ? Justifier.
un+1 = 0,8 un +2 ; un+1 / un n'est pas constant ; la suite n'est pas géométrique.
Partie B.
On considère la suite v définie pour tout n entier naturel par vn = un -10. v0 = -7.
On admet que la suite vn est géométrique de raison 0,8.
1. Démontrer que un = -7 x 0,8n +10.
vn = -7 x 0,8n ; un = vn +10 =10-7 x 0,8n .
2. Déterminer la limite de la suite u et interpréter.
-1 < 0,8 < 1, alors 0,8n tend vers zéro quand n tend vers plus l'infini.
Au bout d'un temps suffisamment long, la quantité de médicament dans le sang est égale à 10 UI.
3. Un laboratoire recommande de ne pas dépasser 8 UI. Déterminer le nombre maximal d'injections possibles.
10-7 x 0,8n < 8 ; 2 < 7 x 0,8n ; 2 / 7 < 0,8n ;
ln(2 /7) < n ln(0,8) ; n < ln(2 /7) / ln(0,8) ; n < 5,6 soit n < 5.
|
...
|
....
|
Exercice 3.
On
se propose d'étudier le refroidissement du café. On dispose d'une tasse
de café à 100°C que l'on place dans une salle où règne une température
constante de 20°C.
Partie A.
On mesure la température q du café à différents instants t. Afin de réaliser un ajustement affine, on pose z = ln q.
temps (min)
|
0
|
1
|
2
|
5
|
12
|
15
|
20
|
35
|
60
|
température q (°C)
|
100
|
90
|
85
|
70
|
50
|
42
|
35
|
27
|
20
|
ln(q)
|
4,605
|
4,500
|
4,443
|
4,248
|
3,912
|
3,738
|
3,555
|
3,296
|
2,996
|
1. Donner une équation de la droite d'ajustement de z en t.
z = -0,027t +4,37.
2. Justifier que la température du café au bout de 10 minutes est d'environ 60°C.
z = -0,027 x10 +4,37 =4,10 ; q = e4,10 ~60.
3. Ce modèle est-il pertinent pour estimer la température du café au bout de 2 heures ?
z = -0,027 x120 +4,37 =1,13 ; q = e1,13 ~3,1 °C.
Ce modèle ne convient pas pour estimer la température du café au
bout de 2 heures.. Au bout de 2 heures, le café est à la température de
la salle..
Partie B.
D'après
la loi de Newton, l'équation différentielle (E) : y'(t) +0,1 y(t) = 2
permet de modèliser la température du café en fonction du temps (
minute).
1. Résoudre cette équation.
Solution générale de y'(t) +0,1 y(t) =0 : y(t) = A e-0,1t avec A une constante.
Solution particulière de (E) : y= 2 /0,1 = 20.
Solution générale de (E) : y(t) = A e-0,1t +20.
2. Déterminer la solution vérifiant f(0) = 100.
100 = A +20 ; A = 80.
f(t) = 80e-0,1t +20.
3. Déterminer la température de la tasse au bout de 10 minutes.
y(10) = 80 e-1 +20 ~49 °C.
4. Résoudre 80e-0,1t +20 < 35. Interpréter.
80e-0,1t < 35 -20 ; 80e-0,1t < 15 ;
e-0,1t < 15 / 80 ; -0,1t < ln(15 /80) ; 0,1t > ln(15 /80).
t > ln(15 /80) /0,1 ; t >16,7 minutes.
Au bout d'environ 17 minutes, la température du café est inférieure à 35°C.
5. On admet que la limite de e-0,1t en plus l'infini est égale à zéro. Déterminer la limite de f et interpréter.
f(t) = 80e-0,1t +20.
f(t) tend vers 20°C au bout d'un temps suffisamment long, température de la salle.
Exercice 4.
On considère la fonction f définie sur ]0 ; 1] par : f(x) = 5 ln(x) -10x +10.
On donne la représentation de la courbe correspondant à f.
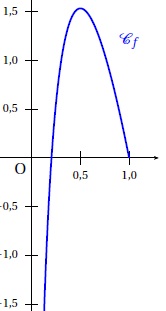
1.a Quelle conjecture peut-on faire quant aux variations de f ?
La fonction est strictement croissante puis strictement décroissante. Le maximum correspond à x = 0,5.
1.b. Quelle conjecture peut-on faire sur la limite de f en 0 ?
f tend vers moins l'infini quand x tend vers zéro.
2. Démontrer que f '(x)= 5(1-2x) / x.
f '(x) = 5 / x -10 = (5-10x) / x = 5(1-2x) / x.
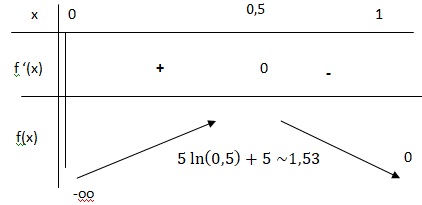
3. Démontrer les conjectures précédentes.
f '(x) est du signe de 1-2x.
4. On considère l'algorithme suivant :
x = 0,4
M=f(0,4)
Pour i allant de 1 à 12
x = x+0,05
y = f(x)
Si y > M
alors M=y
Fin Si
Fin Pour
a. Comléter le tableau suivant.
i
|
|
1
|
2
|
3
|
4
|
x
|
0,4
|
0,45
|
0,50
|
0,55
|
0,60
|
y
|
|
1,507
|
1,534
|
1,511
|
1,446
|
M
|
1,419
|
1,507
|
1,534
|
1,534
|
1,534
|
b. Quelle est la valeur de M à la fin de l'exécution de l'algorithme ? Que représente-t-elle pour la fonction f ?
M contient l'ordonnée du maximum de la fonction f(x), soit environ 1,534.
|
|