Mathématiques,
bac STI2D et STL Métropole 09 / 2020.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
..
..
|
.
.
|
..
..
......
...
|
Exercice
1. QCM
1. Le plan complexe est muni d'un repère orthonormé direct.
Le point A d'affixe zA = -1 +i 3½ et le point B a pour affixe zB = 2 exp(-i 2p / 3).
a. Les points A et B sont confondus.
b. Les points A et B sont symétriques par rapport à l'origine du repère.
c. Les points A et B sont symétriques par rapport à l'axe des abscisses du repère. Vrai.
d. Les points A et B sont symétriques par rapport à l'axe des ordonnées du repère.
Module de zA : |zA| =( (-1)2 +3)½ = 2.
zA / |zA| = -0,5 + i 3½ / 2 =cos (2p/3) + i sin (2p/3) ;
zA = 2 exp(i 2p / 3).
2. Une forme exponentielle de 2 exp(ip/6) x 2i est :
a. 4 exp(i 2p/ 3). Vrai.
b. 4 exp(i p/ 12) .
c. 4 exp(i 5p/ 12) .
d. 4 exp(-i 2p/ 3) .
i = exp(i p /2) ; exp(ip/6) x i = exp(ip/6) xexp(i p /2).
p/6 +p / 2 = p/6 +3p / 6 =4p / 6 =2p / 3.
2 exp(ip/6) x 2i = 4 exp(i 2p/ 3).
3. La valeur exacte de l'intégrale 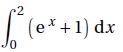 est : est :
2 ; e2-1 ; e2+1 Vrai ; e2+2.
Primitive de f(x)=ex+1 : F(x) = ex+x.
F(2)-F(0)=e2+2-1 = e2+1.
4. Soit g la fonction définie sur R par g(x) =e-2x+10. Cette fonction g est une solution de l'équation différentielle :
y' = y ; y'+2y =0 ; y'-2y = 10 ; y'+2y = 20 Vrai.
g'(x) = -2e-2x ; y' = y est faux.
-2e-2x +2(e-2x+10) = 20 ; y'+2y =0 est faux.
-2e-2x -2(e-2x+10) = -4e-2x-20 ; y'-2y = 10 est faux.
-2e-2x +2(e-2x+10) =20
Exercice 2. 6 points.
Léo envisage l'achat d'un téléphone portable dont la capacité de
stockage est de 32 Go. Selon la notice, la configuration initiale du
téléphone nécessite 20% de cette capacité pour le système
d'exploitation.
1. Calculer le nombre de gigaoctets utilisés par le sysème d'exploitation après la configuration initiale du téléphone.
32 x0,20 = 6,4 Go.
En raison des différentes mises à jour, Léo estime que le nombre de
gigaoctets utilisés par le système d'exploitation augmente de 0,5 % par
mois.
2. On note u0 le nombre de Go utilisés par le système d'exploitation après la configuration initiale. Ainsi u0 = 6,4.
Pour tout entier naturel n > 1, on note un le nombre de Go utilisés par le système d'exploitation, n mois après la configuration initiale.
a. Montrer que u1 = 6,432 et interpréter.
u1 = u0 x(1 +0,005) =6,4 x1,005 =6,432.
Un mois après la configuration initiale, le système d'exploitation utilise 6,432 Go.
b. Montrer que la suite (un) est géométrique dont on précisera la raison.
un+1 / un = 1,005 , suite géométrique de raison 1,005.
c. Exprimer un en fonction de n.
un = 6,4 x1,005n.
d. Calculer le nombre de gigaoctets utilisés par le système 2 ans après la configuration initiale.
u24 = 6,4 x1,00524 ~7,2 Go.
Léo estime que pour utiliser son téléphone dans de bonnes conditions,
celui-ci doit disposer d'une capacité de stockage disponible d'au moins
4 Go.
e. Déterminer le plus petit entier n vérifiant l'inéquation 6,4 x1,005n > 28 et interpréter.
1,005n > 28 / 6,4 ; n ln(1,005) > ln(28 / 6,4) ; n > ln(28 / 6,4) / ln(1,005) ; n >296.
296 /12=24 ans et 8 mois.
Au bout de 296 mois, le téléphone ne sera plus utilisé dans de bonnes conditions.
Léo estime que, chaque mois, les nouvelles photos et les nouveaux
messages occuperont 450 Mo supplémentaires. Il décide de ne rien
supprimer.
3. Pour tout entier naturel n, on note vn
le nombre de Go utilisés par le système d'exploitation, les photos et
les messages au bout de n mois après la configuration initiale. Ainsi v0 = 6,4.
a. Justifier que vn = 6,4 x1,005n +0,45 n.
Au mois n, le système nécessite 6,4 x1,005n et les photos et messages occupent 0,45n Go supplémentaires.
b. Calculer le nombre de Go utilisés deux ans après la configuration initiale.
v24 = 6,4 x1,00524 +0,45 x24 ~7,214 +10,8 ~ 18,0 Go.
c. Léo écrit l'algorithme suivant :
n <-- 0
v <-- 6,4
Tant que v < 28
n <-- n+1
v <-- 6,4 x1,005n+0,45n
Fin Tant que
Que représente le contenu de la variable n à la fin de l'exécution de l'algorithme ?
Au bout du n-ième mois, le téléphone ne sera plus utilisé dans de bonnes conditions.
d. Au bout de combien de mois le téléphone de Léo n'aura-t-il plus suffisamment de capacité de stockage ?
v45 = 28,26 ; v44 =27,77.
Au bout de 45 mois le téléphone ne sera plus utilisé correctement.
4. Pour un téléphone d'une capacité de stockage de 64 Go, on admet que la configuration initiale nécessite 10 Go.
Avec une telle capacité de stockage, Léo pourrat-il utiliser ce
téléphone dans de bonnes conditions deux fois plus longtemps que le
modèle de 32 Go ?
v90=10 x1,00590 +0,45 x 90 =15,67 +40,5 ~56,2 Go.
Léo estime que pour utiliser son téléphone dans de bonnes conditions,
celui-ci doit disposer d'une capacité de stockage disponible d'au moins
4 Go.
56,2 +4 = 60,2 Go, valeur inférieure à 64 Go. Réponse : oui.
|
...
|
....
|
Exercice 3. 5 points.
Les résultats seront arrondis à 10-3 près.
Une voie de chemin de fer relie deux gares A et B sur une distance de 360 km.
La gare A est située au kilomètre 0 et la gare B au kilomètre 360.
Partie A.
Sur
cette voie circule une locomotive destinée au transport des
marchandises. Cette locomotive peut tomber en panne entre A et B.
Lorsque cela se produit, la distance, en km, entre la gare A et le lieu
de la panne est une variable notée D.
On admet que D suit la loi uniforme sur l'intervalle [0 ; 360].
1. Déterminer P(D = 50).
La probabilité d'obtenir une valeur précise est nulle, la loi étant continue. P(D = 50) = 0.
2.
Cette voie passe par un tunnel dont l'entrée est située à 10 km de A et
la sortie à 15 km de A. Calculer la probabilité que la locomotive tombe
en panne dans ce tunnel.
(15-10) / 360 = 0,0139.
3.
La probabilité que la locomotive tombe en panne avant le kilomètre 200
est-elle le double de la probabilité qu'elle tombe en panne avant le
kilomètre 100 ?
P( panne avant le km 100) = 100 / 360 = 5 / 18.
P( panne avant le km 200) = 200 / 360 = 5 / 9 = 2 x 5 / 18. Réponse : oui.
Partie B.
Sur
une période de 4 semaines, on s'intéresse aux trains de voyageurs sur
la même voie, partant de A et arrivant avec un léger retard en B (
retard de moins de 10 min ). Ces retards sont indépendants les uns des
autres. La probabilité qu'un train arrive avec un léger retard
est de 0,02.
Il y a 16 trajets par jour du lundi au vendredi, 12 trajets le samedi et 8 trajets le dimanche.
1. Vérifier que sur ces 4 semaines, 400 trains circulent entre A et B.
4 ( 16 x5+12+8) =400.
Sur cette voie, le nombre de trains en légers retard est une variable aléatoire notée X.
2.a. Préciser ces paramètres.
n = 400 ; p = 0,02 ; q = 1-p = 0,98.
2.b. Déterminer la probabilité qu'exactement 5 trains arrivent en léger retard sur cette période.
P(X =5) =0,091.
3. On décide d'approcher la loi binomiale précédente par la loi normale d'espérance µ=8 et d'écart type s = 2,8.
a. Justifier ces choix.
µ = n p = 400 x0,02 = 8 ; s = (npq)½ = (400 x0,02 x0,98)½ =2,8.
b. Calculer P(4 < X <12).
P(X < 4) =0,07656 ; P(X < 12) =0,9234 ; P(4 < X <12) = 0,9234 -0,07656 ~0,847.
c. Déterminer la probabilité qu'il y ait au moins 4 trains en léger retard.
1-P(X < 4) =1-0,07656 ~0,923.
4. Durant ces 4 semaines, 11 trains sont en léger retard. Cette
observation remet-elle en cause le pourcentage de trains ayant un léger
retard estimé à 2 % ?
On recherche un intervalle de fluctuation asymptotique au seuil de 95 %.
1,96 [(p(1-p) / n ]½ =1,96 [0,02 x0,98 / 400]½ =0,0137.
[0,02-0,0137 ; 0,02 +0,0137] soit [0,0063 ; 0,0337] ou [0,6 % ; 3,4 %].
Fréquence observée : 11 / 400 =0,0275 ou 2,7 %.
Cette valeur appartient à l'intervalle de fluctuation ; cette
observation ne remet pas en cause le pourcentage de trains en léger
retard.
Exercice 4.
Un signal Wi-Fi est émis avec une puissance de 20 décibels-milliwatt ( dBm). L'atténaution du signal dépend :
de la fréquence F du signal ( GHz); de la distance D en mètre parcourue par le signal et des matériaux traversés.
Pour une distance D > 1 m et en l'absence d'obstacle, cette atténuation est donnée par : 32,35+8,7 ln( Fx D).
F =2,4 GHz.
1. Montrer qu'une approximation de l'atténuation de la puissance du signal peut être donnée par A = 40 +8,7 ln(D).
A =32,35+8,7 ln( 2,4 D) =32,35 +8,7 ln(2,4) +8,7 ln(D) ~40 +8,7 ln(D).
2.a. Déterminer A pour une distance D = 10 m.
A = 40 +8,7 ln(10) ~60 dBm.
2.b Pour quelle valeur de D la valeur de A est-elle de 80 dBm ?
40 +8,7 ln(D) = 80 ; ln(D) = 40 / 8,7 =4,598 ; D ~99 m.
3.
Une valeur approchée P de la puissance du signal, en dBm, à une
distance D de l'émetteur est donnée par P = 20 -A. Justifier que P =
-20-8,7 ln(D).
P = 20 -(40+8,7ln(D) = -20-8,7 ln(D).
Dans la suite, la puissance du signal, en dBm, est modélisée par la
fonction f définie sur [1 ; 400] par : f(x) = -20-8,7 ln(x), où x est
la distance en mètre, parcourue par le signal.
4.a. Déterminer f '(x).
f '(x) = -8,7 / x.
4.b. Etudier le signe de f '(x) et en déduire le sens de variation de f.
x étant positif sur [1 ; 400], f '(x) est négative et f(x) est strictement décroissante.
5.a Montrer que f(2x) = f(x) -8,7 ln(2).
f(2x) = -20-8,7 ln(2x) = -20 -8,7 ln(2) -8,7 ln(x) =f(x) -8,7 ln(2).
5.b. Lorsque la distance parcourue par le signal est doublée, de combien de dBm la puissance du signal diminue-t-elle ?.
f(2x)-f(x) = -8,7 ln(2) ~ -6,0 dBm.
6. Le tableau suivant indique la qualité du signal en fonction de sa puissance.
Puissance du signal
|
Qualité du signal
|
Supérieure à -50 dBm
|
excellente
|
Comprise entre -60 et -50 dBm
|
bonne
|
Comprise entre -70 et -60 dBm
|
moyenne
|
inférieure à -70 dBm
|
faible
|
a. Quelle est la qualité du signal lorsqu'il a parcouru 10 m ?
f(x) = -20-8,7 ln(10) ~ -40 dBm, valeur supérieure à -50 dBm, donc qualité excellente.
b. Résoudre f(x) = -60.
-60 = -20-8,7 ln(x) ; -40 = -8,7 ln(x) ; ln(x) = 40 / 8,7 ~4,60 ; x ~99 m.
c. En déduire la distance maximale pour laquelle la qualité du signal est bonne.
La qualité du signal est bonne jusqu'à une distance de 99 m.
|
|