Mathématiques,
bac STI2D biotechnologies Métropole 09 / 2020.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
..
..
|
.
.
|
..
..
......
...
|
Exercice
1. QCM. 4 points.
On considère la fonction f définie sur [-1 ; 3 ] dont la courbe représentative C est donnée. On note f ' sa dérivée.
La tangente à C au point A(1 ; 0) passe par le point de coordonnées (0 ; 3).
F désigne une primitive de f.
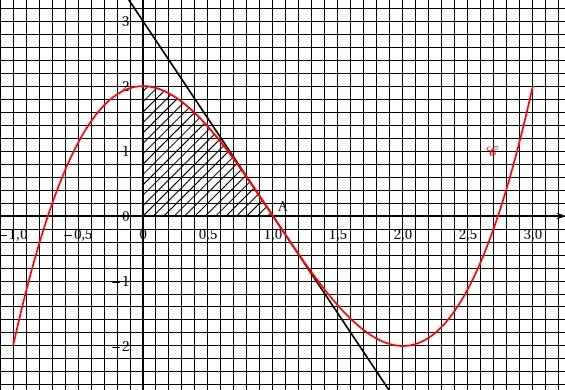
Affirmation 1. L'équation f(x) =0 admet trois solutions dans [-1 ; 3]. Vrai.
La courbe C coupe en trois endroits l'axe des abscisses.
Affirmation 2. L'équation f '(x) =0 admet trois solutions dans [-1 ; 3]. Faux.
La courbe présente seulement deux extrémums.
b. Les points A et
B sont symétriques par rapport à l'origine du repère.
Affirmation 3.  Vrai. Vrai.
L'aire hachurée est comprise entre 1 et 2 unités d'aire.
Affirmation 4. La fonction F est décroissante sur [0 ; 1]. Faux.
f(x) est la dérivée de F(x) ; f(x) est positive sur [0 ; 1], donc F(x) est croissante sur cet intervalle.
Exercice 2. 6 points.
Une
agence de sondage s'est vu confier une enquète sur la proportion de
personnes consommant du café quotidiennement selon leur âge.
Partie A.
Tranche d'âge
|
[20 ; 30 [
|
[30 ; 40[
|
[40 ; 50[
|
[50 ; 60[
|
[60 ; 70[
|
xi
|
25
|
35
|
45
|
55
|
65
|
yi ( pourcentage de consommateurs de café)
|
42
|
50
|
65
|
72
|
84
|
1. Représenter le nuage de points (xi, yi).
2. Déterminer une équation de la droite D d'ajustement de y en x et la tracer sur le graphique.
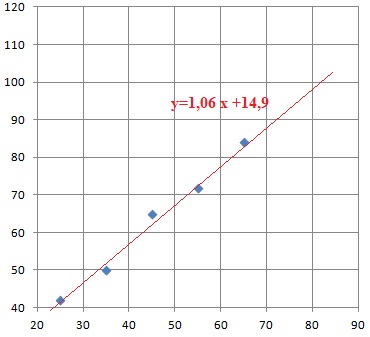
3. Ce modèle est-il adapté pour la tranche d'âge [80 ; 90[. Justifier.
y =1,06 x 85+14,9 =105 %.
Non, un pourcentage ne peut pas dépasser 100.
Partie B.
La consommation annuelle de café dans le monde était de 9,564 millions
de tonnes en 2018. Entre 2012 et 2018, cette consommation a augmenté
d'environ 1,3 % en moyenne par an.
Pour tout entier naturel n, on note cn la consommation mondiale de café en millions de tonnes pour l'année 2018 +n. Donc c0 = 9,564.
On suppose que cette consommation continue d'augmenter de 1,3 % tous les ans.
1. Calculer c1 et interpréter.
c1 = 1,013 x9,564 =9,688.
La consommation annuelle de café dans le monde sera de 9,688 millions de tonnes en 2019.
2. Justifier que la suite est géométrique et donner ces caractéristiques.
cn+1 / cn = 1,013 ; suite géométrique de raison 1,013 et de premier terme c0 = 9,564.
3.a. Exprimer cn en fonction de n.
cn = 9,564 x1,013n.
b. En déduire la consommation annuelle de café en 2032.
n =14 ; c14 = 9,564 x1,01314~11,460.
4.
On souhaite savoir à partir de quelle année la consommation annuelle de
café dépassera 16 millions de tonnes. Compléter l'algorithme suivant et
donner le résultat.
N désigne l'année et C la consommation de café.
N <--0
C <--9,564
Tant que C < 16
N<--N+1
C<--C*1,013
Fin Tant que
N =2018+N
9,564 x1,013n > 16 ; 1,013n > 16 / 9,564.
n ln(1,013) > ln(16 / 9,564) ;
n > ln(16 / 9,564) / ln(1,013) ; n >39,84 soit 40 (année 2018+40 soit 2058).
|
...
|
....
|
Exercice 3. 5 points.
Partie A.
Dans
une fabrique de bonbons, les bonbons TROBONS constituent le produit
phare. Chaque paquet contient 200 bonbons conditionnés en 10 paquets
individuels de 20 bonbons. Le paquet d'emballage pèse 4 g et les paquets
individuels 1 gramme.
On modélise la masse d'un bobon par une variable aléatoire B qui suit
la loi normale de moyenne 5 et d'écart type 0,08. Les bonbons sont
rejetés si leur masse n'est pas comprise entre 4,77 g et 5,23 g.
1. On choisit un bonbon au hasard. Quelle est la probabilité qu'il soit accepté ?
P(B < 4,77) =0,0020 ; P(B < 5,23) =0,998 ; P(4,77 < B < 5,23) =0,998-0,002=0,996.
2. Un responsable qualité affirme qu'au moins 99 % des bonbons pèse plus de 4,8 g. A t-il raison ? Justifier.
P(B > 4,8 ) =1-P(B < 4,8) = 1-0,0062 =0,9938. Il a raison.
3. Quelle est la masse moyenne d'un paquet de bonbons ?
200 x 5 +4 +10 =1014 g.
Partie B.
On s'intéresse à la qualité des bobons avant leur mise en sachets.
On admet que la probabilité qu'un bonbon soit impropre à la vente est
égale à 0,004. On prélève au hasard 200 bonbons en fin de chaîne de
production. On suppose que la production est suffisamment importante
pour assimiler ce prélèvement à un tirage avec remise.
On note X la variable aléatoire qui, à chaque prélèvement de ce type, associe le nombre de bonbons impropre à la vente.
Les paquets de bonbons doivent contenir au plus trois bonbons impropres à la vente. On tire au hasard 200 bonbons.
Déterminer la probabilité que le paquet qui les contient soit accepté par le service qualité.
X suit une loi binomiale de paramètre n = 200 ; p = 0,004 ; q = 1-p =0,996.
P(X=0)= 0,4486 ; P(X=1) =0,3603 ; P(X=2)=0,1440 ; P(X=3) =0,0382.
Probabilité que le paquet soit accepté : 0,4486 +0,3603 +0,1440 +0,0382 ~0,991.
Partie C.
La fabrique de bonbons s'interroge sur la suppression des paquets
individuels. Le service développement durable lance une enquète sur un
échantillon de 800 consommateurs pour estimer l'influence sur les
ventes d'une éventuelle suppression des sachets individuels. Parmi ces
800 consommateurs, le nombre de clients qui achèteraient ce produit
avec les sachets individuels est de 735 et le nombre de clients
qui achèterait le produit sans sachets individuels est de 720.
1. Déterminer un
intervalle de confiance à 95 % de la proportion de clients qui
acheterait le produit avec ou sans sachets individuels.
1/ n½ =1 / 800½=0,0354.
Intervalle de confiance pour les clients qui acheterait les bonbons avec sachets individuels :
Fréquence f = 735 / 800 =0,9188.
[0,9188 -0,0354 ; 0,9188 +0,0354] soit [0,883 ;0,954 ].
Intervalle de confiance pour les clients qui acheterait les bonbons sans sachets individuels :
Fréquence f = 720 / 800 =0,900.
[0,900 -0,0354 ; 0,900 +0,0354] soit [0,865 ;0,935 ].
2. Au niveau de confiance de 95 %, peut-on penser que la suppression des sachets est réalisable ?
Les deux intervalles se recoupent. Il n'y aura pas d'influence sur les ventes.
Exercice 4.
Un bassin d'eau contenant 50 000 m3 a subi une pollution aux nitrates. Des mesures ont permis d'estimer qu'à un instant t0
la concentration en nitrate est de 10 000 mg / L. Un travail de
dépollution est mis en oeuvre et on note f(t) la concentration en
nitrate dans l'eau, en mg / L, à l'instant t exprimé en heure, en
prenant t0=0.
Partie A.
On admet que la fonction f est solution de l'équation différentielle E : y' +0,2y=8.
1. Déterminer les solutions de E.
Solution générale de y'+0,2y=0 : f(t) = A e-0,2t avec A une constante.
Solution particulière de E : f(t) =40.
Solution générale de E : f(t) = 40+Ae-0,2t.
2.a. Expliquer pourquoi f(0) = 10 000.
La concentration initiale en nitrate est 10 000 mg / L.
2.b En déduire l'expression de f.
10 000 = 40 +A. A = 9960.
f(t) = 9960 e-0,2t +40.
Partie B.
On admet que f(t) = 9960 e-0,2t +40.
1.a. Calculer la fonction dérivée f '(t) de la fonction f(t).
f '(t) = -0,2 x 9960e-0,2t = -1992 e-0,2t .
1.b. Vérifier que la concentration de polluant est décroissante dans le temps.
e-0,2t est positif ; f '(t) est négative sur [0 ; +oo[.
f(t) est strictement décroissante sur cet intervalle.
2. Préciser la limite de f(t) en plus l'infini et interpréter.
En plus l'infini, e-0,2t tend vers zéro et f(t) tend vers 40.
Au bout d'un temps suffisamment long, la concentration en nitrate est constante égale à 40 mg / L.
3. Une eau est considérée comme potable lorsque la concentration en nitrate est inférieure à 50 mg / L.
Combien de temps au minimum doit-on attendre pour atteindre cette concentration ?
9960 e-0,2t +40 < 50 ; 9960 e-0,2t < 10 ; e-0,2t < 10/ 9960 ;
-0,2t < ln(10 /9960) ; t > ln(996) / 0,2 ; t >34,519 heures ou 34 heures 31 minutes.
|
|