Mathématiques,
bac STI2D biotechnologies Nlle Calédonie 12 / 2020.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
..
..
|
.
.
|
..
..
......
...
|
Exercice
1. QCM 4 points.
Dans les deux premières questions, on considère la fonction f définie sur R par f(x) =(x+2)e-2x.
La courbe C représentative de f est donnée.
Soit les points A(0 ; 2) et B(1 ; -1). La droite (AB) est tangente à C au point A.
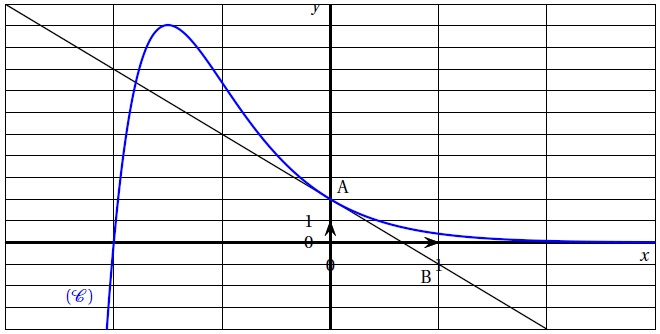
1. f '(0) est égale à : 2 ; -3 vrai ; -1 ; -1,5.
f '(0) est le coefficient directeur de la droite (AB) ; f '(0) = -3.
2.
L'ensemble des solutions de l'équation f '(x) = 0 est : 2 ; 3 ; -2 ; -1,5 vrai.
La courbe présente un maximum ( f '(x) =0 ) pour = -1,5.
Dans les deux questions suivantes, on s'intéresse à la greffe de cornée en France.
47,6 % des inscrits en 2015 en Ile de France ont reçu une greffe de
cornée la même année. On choisit au hasard 100 inscrits en 2015. Ce
choix est assimilable à un tirage avec remise.
On note X la variable aléatoire qui compte le nombre de personnes
greffées dans ce groupe. X suit une loi binomiale de paramètres 100 et
0,476.
3. La probabilité d'avoir au moins 40 personnes greffées est :
0,077 ; 0,651 ; 0,948 ; 1,027.
Au moins 40 personnes greffées signifie 40 et plus de 40.
P(X >40)=1-P(X < 40)= 1-0,077=0,923 ~0,948.
4. Les conditions sont satisfaisantes pour approchées la loi de X par une loi normale d'une variable aléatoire Y.
P(37 < Y < 58 )~ 0,038 ; 0,872 ; 0,853 ; 0,964 vrai.
Paramètres de cette loi normale : µ = 100 x0,476 = 47,6 ; écart type s =(100 x0,476 x(1-0,476))½~5,0.
P(Y < 37) =0,017 ; P(Y < 58) =0,981 ; P(37 < Y < 58 )~ 0981-0,017 ~0,964.
Exercice 2. 5 points.
Suite
à un accident nucléaire, des traces de contaminations ont été
découvertes lors des contrôles réalisés à la sortie des zones
nucléaires grâce au passage sous des portiques d'accès. Le tableau
suivant donne les résultats fournis, heure par heure, par un appareil
de mesure de la radioactivité. Ni représente le nombre de particules recueillies par l'appareil en une seconde.
1. Compléter la troisième ligne du tableau.
ti (heure)
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
Ni
|
170
|
102
|
63
|
39
|
24
|
16
|
9
|
| zi = ln(Ni). |
5,14
|
4,62
|
4,14
|
3,66
|
3,18
|
2,77
|
2,20
|
2 et 3 et 4 Représenter le nuage de points de coordonnées (ti ; zi) ; donner l'équation de la droite de régression linéaire de z en t. La représenter.
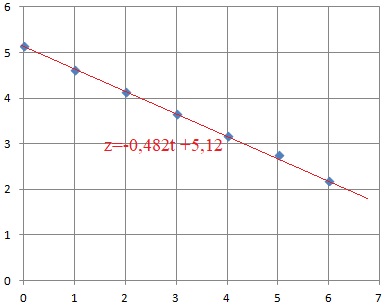
5. En déduire l'expression de N en fonction de t.
N = exp(z) =exp(-0,48t +5,12).
6. L'appareil
possède deux voyants, un rouge et un vert. Tant que le nombre de
particules recueillies est strictement supérieur à 3, le voyant rouge
est allumé. Lorsque le nombre de particules recueillies est inférieur
ou égal à 3, le voyant rouge s'éteinf et le voyant vert s'allume.
Déterminer le nombre d'heure nécessaires pour voir le voyant vert
s'allumer.
exp(-0,48t +5,12) < 3 ; -0,48 t +5,12 < ln(3) :
-0,48 t < ln(3)-5,12 ; t > [-ln(3)+5,12] / 0,48 ; t >8,37 heures.
|
...
|
....
|
Exercice 3. 5 points.
On introduit initialement 200 bactéries dans un milieu clos. On s'intéresse à l'évolution de la population de bactéries.
Partie A. Un premier modèle.
On note un la population de bactériies présentes dans ce milieu, n heures après l'introduction des bactéries. Ainsi u0 = 200.
Selon le modèle proposé par Malthus, la suite (un) vérifie, pour tout entier n : un+1 = un +aun+bun.
a=0,12 taux de natalité et b=0,07 taux de mortalité.
1. a. Déterminer le nombre de bactéries 1 heure après le début de l'expérience.
u1 = 200 +0,12 *200-0,07 *200 =210.
b. Montrer que la suite est géométrique de raison 0,05.
un+1 =un(1+0,12-0,07) =1,05 un.
c. En déduire l'expression de un en fonction de n.
un = u0 *1,05n = 200 *1,05n.
2. Compléter le tableau suivant :
n
|
0
|
1
|
5
|
10
|
20
|
40
|
60
|
100
|
un
|
200
|
210
|
255
|
326
|
531
|
1408
|
3736
|
26301
|
3.a. Déterminer la limite de un. Justifier.
1,05 étant supérieur à1, 1,05n tend vers plus l'infini quand n tend vers l'infini.
un tend donc vers l'infini.
b. Ce modèle paraît-il réaliste J Justifier.
Ce modèle n'est pas réaliste : quand le nombre de bactéries devient
trop grand, la nourriture vient à manquer et les bactéries meurent.
Partie B. Deuxième modèle.
Le taux de natalité et de mortalité dépendent de la population.
On note vn la population de bactéries dans ce milieu n heures après l'introduction de v0 = 200 bactéries et on admet, que pour tout entier naturel n :
vn+1=1,12 vn -0,0001vn2.
1. On considère l'algorithme ci-dessous :
V<--200
N<-- 0
Tant que V < 1100
V<--1,12*V-0,0001*V2
N<--N+1
Fin Tant que
a. Compléter le tableau en exécutant l'algorithme à la main.
N
|
1
|
2
|
3
|
4
|
V
|
220
|
242
|
265
|
289
|
b.
A la fin de l'éxécution, la variable N contient la valeur 34. Quel est
le rôle de cet algorithme ? Comment peut-on interpréter ce résultat ?
Cet algorithme calcule le nombre d'heures au bout desquelles la population de bactéries atteint la valeur 1100.
Au bout de 34 heures la population de bactéries atteint la valeur 1100.
2.
Le graphe ci-dessous donne la représentation des premiers termes de la
suite (vn). Que peut-on conjecturer quant à l'évolution de cette
population à long terme ?
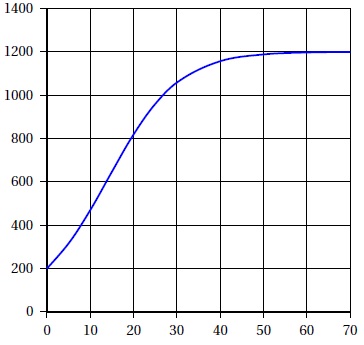
A long terme la population se stabilise vers 1200 bactéries.
Exercice 4. 5
points.
Partie A. Résolution d'une équation différentielle.
On considère l'équation différentielle (E) : 5y'+7,9y=0.
1. Déterminer les solutions de (E).
y'+1,58y = 0.
y = A e-1,58x avec A une constante.
2. Déterminer la solution f de (E) qui vérifie f(0) =0,001.
f(0) = Ae0 = A=0,001.
f(x) = 0,001 e-1,58x.
Partie B. Loi de Beer Lambert.
Un faisceau lumineux incident, d'intensité I0,
traverse une solution contenue dans un tube transparent. A la sortie du
tube, l'intensité I du faisceau lumineux est mesurée par un détecteur.
I(c) = I0 e-edc.
e =1,58 L mol-1 cm-1, coefficient d'extintion molaire du soluté ; c concentration de la substance absorbante ; d= 1 cm épaisseur du milieu traversé.
I0 = 0,001 W sr-1 ( watt par stéradian ).
1. Vérifier que la fonction I(c) est la solution particulière de (E).
I =0,001 e-1,58c = f(x) trouvé ci-dessus.
2. Etudier sur [0 ; +oo[ les variations de la fonction f. Est-ce cohérent dans ce contexte ?.
f '(x) = -0,001x1,58 e-1,58c .
Le terme en exponentielle étant positif, f '(x) est négative et f(c) est strictement décroissante.
Lorsque la concentration de la solution traversée par le faisceau
augmente suffisamment, aucune lumière n'émerge de la solution. C'est
donc cohérent.
3
Déterminer la valeur exacte puis arrondie à 0,01mol/L de la
concentration c permettant de récupérer 75 % de l'intensité du faisceau
incident à la sortie de la cuvette.
I / I0 = 0,75 = e-1,58c ; ln(0,75) = -1,58 c ; c = - ln(0,75) / 1,58 ~ 0,18 mol / L.
4. L'absorbance de la substance est définie par A(c) =ln(I0 / I(c)).
Donner sous forme simplifié, l'expression de l'ansorbance en fonction de c.
I0 / I(c) = e1,58c ; ln(I0 / I(c))=1,58 c ; A = 1,58 c.
Partie C : valeur moyenne.
On admet que l'intensité moyenne du faisceau lumineux lorsque la concentration varie de 0,5 mol /L à 1,3 mol /L est égale à :
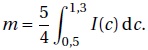
Déterminer la valeur exacte, puis une valeur approchée à 10-4 près, de m.
Primitive de 0,001 e-1,58c : G(c) =-0,001 / 1,58 e-1,58c ;
m =5 /4 ( G(1,3) -G(0,5) = 5 / 4 x(-0,001 / 1,58) (e-1,58*1,3 -e-1,58*0,5).
m = 5 / 4 x0,001 / 1,58 (e-0,79-e-2,054 ).
m ~7,911 10-4 (0,4538 - 0,1282) ~2,6 10-4 W sr-1.
|
|