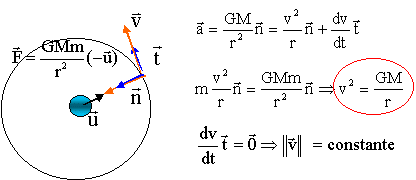La
mission GRACE-FO, Bac Amérique du Nord 2021.
Satellite, champ électrique, interférences, capacité d'un condensateur.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
..
..
|
.
.
|
..
..
......
...
|
A Caractéristiques de l'orbite.
L'orbite des satellites est
quasi-circulaire à l'altitude z = 490 km. L'inclinaison du plan de la
trajectoire sur l'équateur est égale à 89°. On parle d'une orbite
polaire. Les deux satellites jumeaux se déplacent sur la même orbite à
une distance notée L de 220 km l'un de l'autre. Leur altitude leur
permet de parcourir environ 15 fois leur orbite par jour et d'obtenir
une cartographie mensuelle de l'évolution des masses d'eau.
On étudie le mouvement d'un des satellites, de masse m, dans le référentiel géocentrique considéré galiléen.
A.1. Faire un croquis montrant la terre et le satellite sur son orbite.
A.2. Donner l'expression vectorielle de la force exercée par la terre sur le satellite.
A.3. En déduire l'expression du champ de gravitation terrestre.
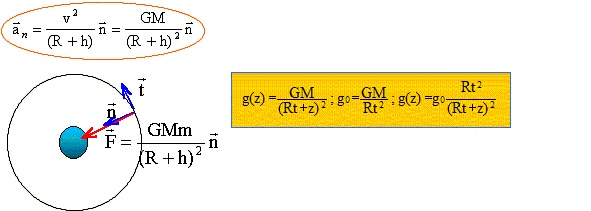
Ce champ est centripète, dirigé vers le centre de la terre et de valeur g= G Mterre / ( Rterre +z)2.
A.4.5.6. Etablir l'exppression vectorielle de l'accélération du satellite.
Montrer que dans le cadre d'un mouvement circulaire, le mouvement du
satellite est uniforme. Donner l'expression de la vitesse du satellite.
On note r = z + Rterre.
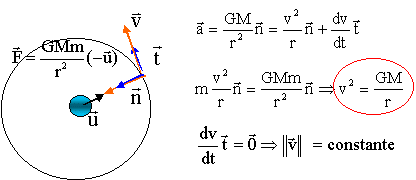
A.7. En
déduire la valeur de la période de révolution du satellite et
vérifier qu'elle est conforme à " leur altitude leur permet de
parcourur environ 15 fois leur orbite par jour".
Circonférence : 2 p(Rterre +z ) = 6,28 (6,371 106 +4,9 105 )=4,31 107 m.
Vitesse : (GM / r)½ = (6,67 10-11 x5,98 1024 /(6,371 106 +4,9 105 ))½ =7,62 103 m /s.
Période T = circonférence / vitesse =4,31 107 / (7,62 103) =5,65 103 s ou environ 1,57 heures.
Nombre de révolutions par jour : 24 / 1,57 ~ 15.
On s'interesse à la situation particulière suivante.
Le satellite de tête passe au-dessus d'une zone où le champ de gravitation g1 n'est pas centripète alors que le 2ème satellite survole une zone où règne un champ de gravitation g2 centripète.
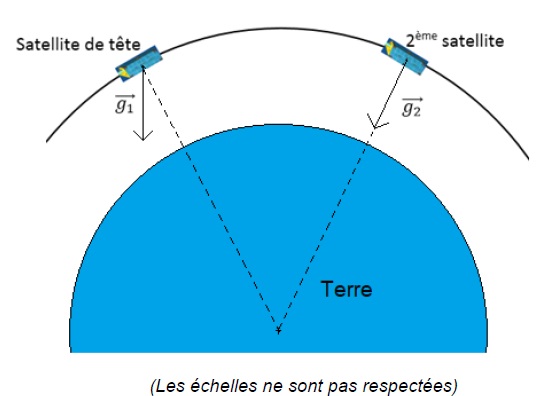
A.8. Dans cette situation, expliquer si la distance L entre les deux satellites reste constante, augmente ou bien diminue.

D'après le dessin, les normes des accélération des deux satellites sont égales.
Vitesse du second satellite : v2, tangente à la trajectoire, valeur : 7,62 103 m /s.
Vitesse du satellite de tête :
- contribution due à l'accélération normale : 0,87½ v2 = 0,93 v2 ;
- contribution due à l'accélération tangentielle : 0,5 g2 t.
v1 = 0,93 v2 +0,5 g2 t.
Si
t est faible, la vitesse du satellite de tête est supérieure à celle du
second satellite : L croît, sinon si t augmente suffisamment, L décroît.
|
....
|
Principe de l'interféromètre embarqué
Le
satellite de tête est affecté en premier par un changement du champ
gravitationnel, cela engendre alors une légère modification de la
distance le séparant du second satellite. La mesure, par
interférométrie, des variations de distance entre les satellites permet
d'accéder à l'évolution du champ gravitationnel dans la région
survolée. Un interféromètre laser, dont une partie est embarquée dans
le satellite de tête et l'autre partie dans le second satellite,
détermine avec une très grande précision la variation de distance,
notée d, entre les deux satellites.
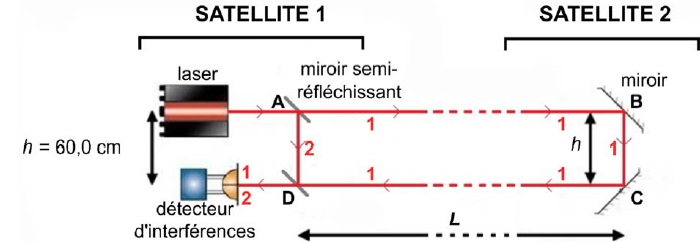
Le faisceau lumineux issu du laser se partage en deux faisceaux au
niveau du miroir semi-réfléchissant A : le faisceau 1 parcourt le
trajet ABCD, et le faisceau 2 parcourt le trajet AD. Les faisceaux
se réunissent en D pour atteindre le détecteur d'interférences.
Longueur du laser dans le vide l = 1064 nm.
1. Justifier que ce dispositif permet d'obtenir des interférences.
Les
interférences à deux ondes sont produites par des dispositifs à
division du front d'onde ( miroir semi-réflichissant dans ce cas).
2. Définir le phénomène d'interférences constructives de deux ondes.
Les interférences sont constructives si elles correspondent à la superposition de deux ondes cohérentes d'amplitude maximale.
La différence de marche entre les deux ondes qui interfèrent doit être égale à un multiple de leur longueur d'onde.
3. Etablir l'expression de la différence de marche d en fonction de L.
d
=AB +BC +CD - AD =AB+CD = 2 L.
Le satellite 1 s'éloigne d'une distance d du satellite 2. Les deux satellites sont maintenant distants de L+d.
4. Montrer que la variation Dd de la différence de marche vaut 2d.
Nouvelle différence de marche d' = 2(L+d).
Dd = d'-d = 2(L+d) -2L = 2d.
Le capteur d'interférennces est capable de repérer au mieux une
variation de différence de marche qui correspond à deux états
immédiatement successifs d'interférennces constructives.
5.
Justifier que la variation de distance d correspondant à deux états
immédiatement successifs d'interférence constructive est égale à ½l.
La
différence de marche entre les deux ondes qui interfèrent de manière
constructive doit être égale à un multiple de leur longueur d'onde.
d = n l ; Pour deux états immédiatement successifs d'interférence constructive, n =1.
Dd =2d = l ; d = ½l.
6. Calculer la plus petite valeur de d détectable.
1064 / 2 =532 nm.
Principe des accéléromètres.
Des
accéléromètres ultrasensibles embarqués à bord des satellites
permettent d'accéder directement aux forces non-gravitationnelles par
la mesure de la variation des capacités de plusieurs condensateurs. Une
masse d'épreuve, maintenue en suspension au centre d'une cage
électrostatique, subit un déplacement lorsqu'elle est soumise à une
force non gravitationnelle. Son déplacement se traduit par la
modification de la capacité de trois paiires de condensateurs.
On étudie le fonctionnement d'un condensateur plan dont la face
de gauche de la masse d'épreuve constitue l'armature mobile, l'autre
armature étant fixée sur la cage électrostatique.
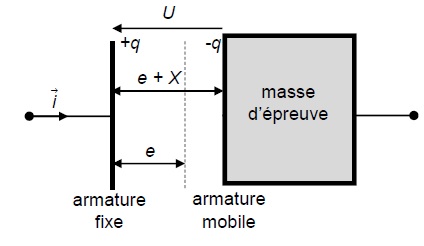
En absennce de forces non gravitationnelles, la distance
entre les deux armatures est notée e. En présennce d'une force
non-gravitationnelle, l'armature mobile subit un déplacement X ( compté
positivement) dans la direction définie par le vecteur unitaire indiqué
sur le schéma.
Capacité d'un condensateur plan : C = e0S / D avec e0 permittivité électrique du vide, S surface des armatures et D distance des armatures.
1. Discuter de l'influence du déplacement X, choisi positif, sur la valeur de la capacité C.
e0S étant constant, si la distance des armatures augmente, la capacité du condensateur diminue.
2. Donner l'expression du champ électrique E créé entre les plaques du condensateur.
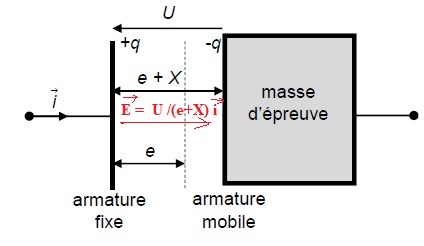
On s'intéresse à la situation où la charge électrique q portée par l'armature fixe est positive.
3.
Identifier le schéma qui, parmi les 4 suivants, représente correctement
le champ E et la force F, action subie par l'armature mobile.
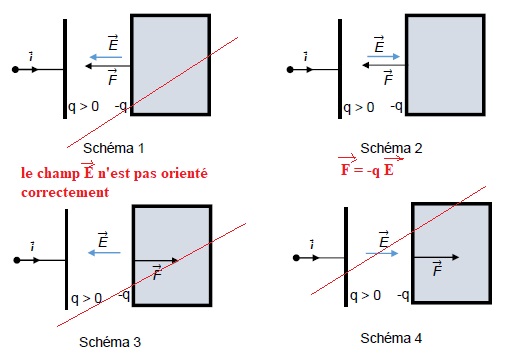
Le condensateur décrit sur le schéma précédent est associé à un second
condensateur. La masse d'épreuve est mobile entre deux armatures fixes,
l'une à gauche, l'autre à droite. Le dispositif est conçu de telle
sorte que la force électrostatique exercée par l'armature fixe de
droite sur la masse d'épreuve est exactement opposée à la force
électrostatique exercée par l'armature fixe de gauche : ces deux forces
se compensent.
4. Etablir la relation existant entre le champ électrique Ed crée par l'armature fixe de droite et le champ électrique Eg crée par l'armature fixe de gauche.
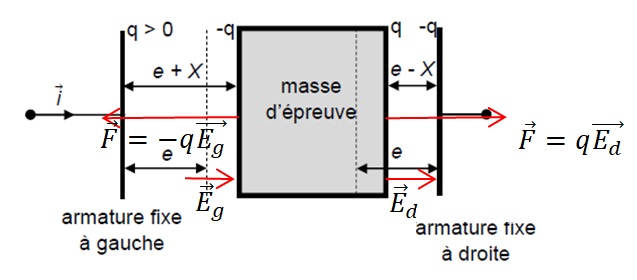
Les deux forces se compensent ; les valeurs absolues des charges q sont
identiques ; les deux champs ont la même direction, le même sens et la
même norme.
|
|