Mathématiques,
DNB Polynésie 2021.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
..
..
|
.
.
|
..
..
......
...
|
Exercice
1. 22 points.
Cet exercice est constitué de 5 questions indépendantes.
1. Sur la figure
ci-dessous, chacun des quadrilatères quad1, quad2 et quad3 est l'image
du quadrilatère TRAP par une transformation.
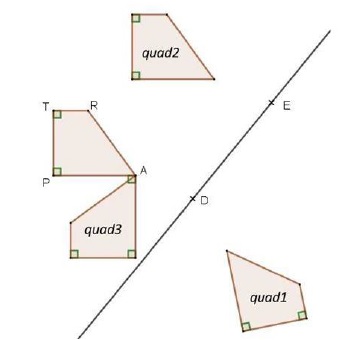
Recopier les trois phrases ci-dessous sur la copie et compléter, sans
justifier, chacune d’elles par le numéro de l’une des transformations
proposées dans le tableau qui suit :
a. Le quadrilatère quad1 est l’image du quadrilatère TRAP par la transformation n° 6.
b. Le quadrilatère quad2 est l’image du quadrilatère TRAP par la transformation n°1.
c. Le quadrilatère quad3 est l’image du quadrilatère TRAP par la transformation n°2.
Transformation n° 1 : translation qui transforme le point D en le point E.
Transformation n° 2 : rotation de centre A et d’angle 90° dans le sens contraire des aiguilles d’une montre.
Transformation n° 3 : symétrie centrale de centre D.
Transformation n+ 4 : translation qui transforme le point E en le point D.
Transformation n° 5 : rotation de centre A et d’angle 120° dans le sens contraire des aiguilles d’une montre.
Transformation n° 6 : symétrie axiale d’axe (DE).
2. Développer et réduire l’expression suivante : (2x−3)(−5+2x)−4+6x.
-10x+4x2+15-6x-4+6x =4x2-10x +11.
3. Résoudre l’équation suivante : (x+6)(5x−2)=0.
x+6 =0 soit x = -6.
et 5x-2=0 soit x = 2 /5.
4. a. Décomposer, sans justifier, en produits de facteurs premiers les nombres 1 386 et 1 716.
1386 =2 x32 x 7 x11.
1716 = 22 x 3 x 11 x13.
b. En déduire la forme irréductible de la fraction : 1 386 / 1 716.
2 x32 x 7 x11 / (22 x 3 x 11 x13) = 3 x7 / (2 x 13) = 21 / 26.
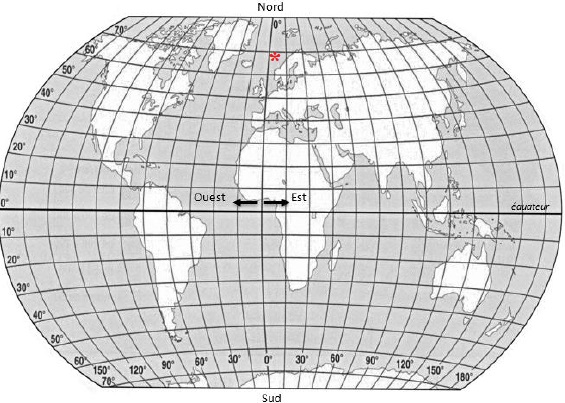
5. Les coordonnées géographiques de la ville appelée Jokkmokk sont environ : 67° Nord et 19° Est.
Placer approximativement la ville de Jokkmokk sur le planisphère.
Exercice 2 (16
points)
Un professeur propose un jeu à ses élèves.
Ils doivent tirer un jeton dans une boîte de leur choix et gagnent
lorsqu'ils tombent sur un jeton noir. Le professeur leur précise que :
- La boîte A contient 10 jetons dont 1 jeton noir.
- La boîte B contient 15% de jetons noirs.
- La boîte C contient exactement 350 jetons blancs et 50 jetons noirs.
Les jetons sont indiscernables au toucher. Une fois que l’élève a choisi sa boîte, le tirage se fait au hasard.
1. Montrer que, dans la boîte C, la probabilité de tirer un jeton noir est 1 / 8.
50 cas favorables sur 400 possibilités soit 50 / 400 = 5 / 40 = 1 /8 = 0,125.
2. C'est le tour de Maxime. Dans quelle boîte a-t-il intérêt à tenter sa chance ? Justifier la réponse.
Probabilité de tirer un jeton noir dans la boîte A : 1 /10 = 0,1.
Probabilité de tirer un jeton noir dans la boîte B : 0,15.
Boîte B.
3. La boîte B contient 18 jetons noirs. Combien y a-t-il de jetons au total dans cette boîte ?
0,15 n = 18 ; n = 18 / 0,15 = 120.
4. On ajoute 10
jetons noirs dans la boîte C. Déterminer le nombre de jetons blancs à
ajouter dans la boîte C pour que la probabilité de tirer un jeton noir
reste égale à 1 / 8 .
60 jetons noirs sur un total de n jetons.
60 / n = 1 /8 ; n = 60 x8 = 480.
On ajoute 480-350 -10= 120 jetons blancs.
Exercice 3 (21
points)
Sur la figure ci-dessous, qui n’est pas en vraie grandeur, le point C est le point d’intersection des droites (BE) et (AD).
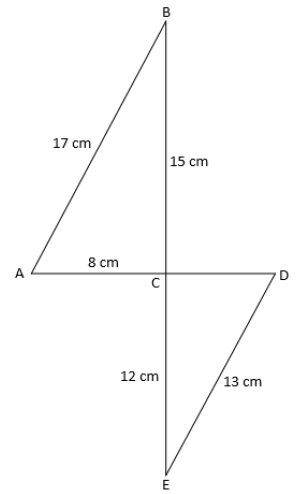
1. Démontrer que le triangle ABC est rectangle en C.
AB2 = 172 =289.
AC2+BC2 = 82+152 =64+225=289.
AB2 =AC2+BC2 .
D'après la réciproque du théorème de Pythagore, le triangle ABC est rectangle en C.
2. Calculer l’aire du triangle ABC.
AC x BC /2 = 8 x15 /2 = 60 cm2.
3. Calculer une valeur approchée au degré près de l’angle BAC.
Tangente de cet angle = BC / AC = 15 / 8 =1,875.
Cet angle mesure environ 62°.
4. Calculer le périmètre du triangle CDE.
CD2 = DE2 -CE2=132-122 =169-144 =25 ; CD = 5 cm.
Périmètre du triangle CDE : 12 +13 +5 = 30 cm.
5. Les droites (AB) et (DE) sont-elles parallèles ?
AC / CD = 8 / 5 =1,6 ; BC / CE = 15 /12 = 1,25.
AC / CD diffère de BC / CE : les droites (AB) et (DE) ne sont pas parallèles.
|
|
....
|
Exercice 4 (19 points)
On donne le programme suivant :
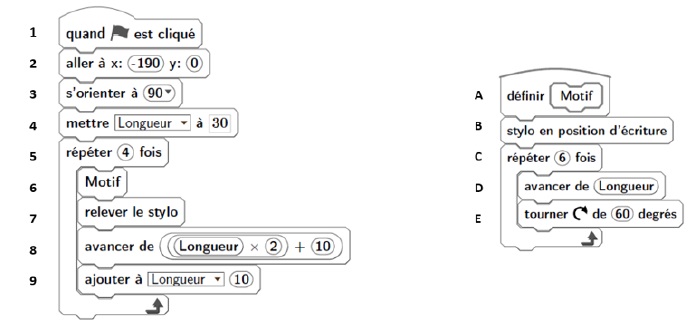
On rappelle que « s’orienter à 90 » signifie que l’on est orienté vers la droite.
1. On prendra dans cette question 1 mm pour un pixel.
Représenter en vraie grandeur sur votre copie la figure que trace le bloc Motif lorsque Longueur vaut 30 pixels.
2. Ce programme utilise une variable, quel est son nom ? À quoi correspond-elle sur la figure réalisée par le bloc Motif ?
La variable " longueur " correspond à la longueur du côté de l'hexagone tracé ci-dessus.
3. Laquelle de ces
trois figures obtient-on lorsqu’on exécute ce programme ? Indiquer sur
la copie le numéro de la bonne proposition parmi les trois suivantes.
On expliquera son choix.

On trace 4 hexagones en se déplaçant à chaque fois de 10 vers le droite et en ajoutant 10 à la variable longueur.
4. Modifier le
programme précédent pour obtenir la figure ci-dessous. Pour cela,
indiquer les numéros des instructions à supprimer ou à modifier, et
préciser les modifications à apporter :

Supprimer la ligne 9.
5. On souhaite
modifier le bloc Motif afin qu’il permette de tracer un carré. Pour
cela, indiquer les lettres des instructions à supprimer ou à modifier,
et préciser les modifications à apporter.
C : répéter 4 fois.
E : tourner de 90° vers la droite.
Exercice 5 (22
points)
Nora
veut ouvrir un magasin de souvenirs à Paris et proposer à la vente des
tours Eiffel miniatures. Elle contacte deux fournisseurs qui lui
envoient chacun sous forme de graphiques le prix à leur payer en
fonction du nombre de tours Eiffel achetées.
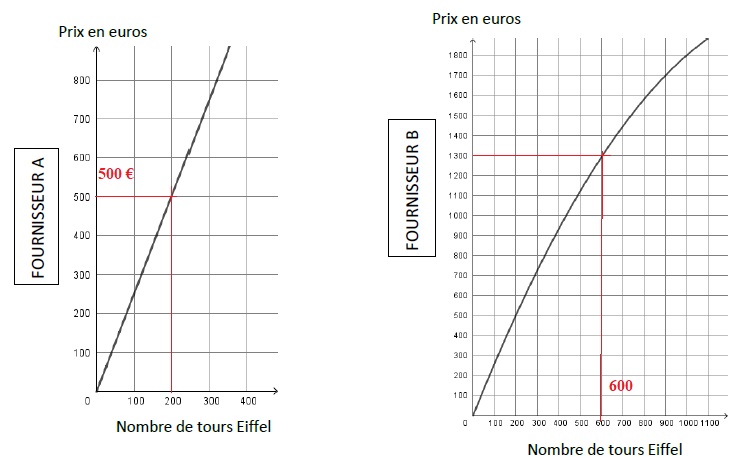
1. Par lecture graphique, avec la précision qu’elle permet, et sans justification,
a. Déterminer le prix à payer pour acheter 200 tours Eiffel chez le fournisseur A.
b. Nora a dépensé 1 300 euros chez le fournisseur B. Combien de tours Eiffel lui a-t-elle achetées ?
2. Ces fournisseurs proposent-ils des prix proportionnels au nombre de tours Eiffel achetées ?
A : le prix est proportionnel au nombre de tours Eiffel acheté, le graphe étant une droite passant par l'origine.
3. a. Pour le
fournisseur A, on admet que le prix des tours Eiffel est donné par la
fonction linéaire 𝑓 représentée ci-dessus. On a en particulier
f(100)=250. Déterminer l’expression de f(x) en fonction de x.
f(x) = a x ; 250 = 100 a ; a = 2,5.
f(x) = 2,5 x.
b. Calculer f(1 000).
f(1000) = 2500.
c. Nora veut acheter 1 000 tours Eiffel. Quel est le fournisseur le moins cher dans ce cas-là ?
B : 1800 . ( le moins cher).
A: 2500 .
4. Nora contacte un
troisième fournisseur, le fournisseur C, qui lui demande un paiement
initial de 150 euros pour avoir accès à ses articles, en plus d’un prix
unitaire de 2 euros par tour Eiffel.
a. Remplir le tableau des tarifs suivant :
nombre de tour Eiffel
|
1
|
100
|
200
|
1000
|
x
|
prix payé fournisseur C
|
152
|
350
|
150 +400 =550
|
2000 +150 = 2150
|
150 +2x
|
.
b. Avec 580 euros, combien de tours Eiffel peut acheter Nora chez le fournisseur C ?
580 = 150 +2x ; 2x = 580-150 =430 ; x = 420/2 = 215.
c. Résoudre l’équation suivante : 2,5 x=150+2x.
2,5 x-2x = 150 ; 0,5 x = 150 ; x = 300.
Expliquer à quoi correspond la solution trouvée.
En achetant 300 tours Eiffel, les fournisseurs A et C proposent le même prix.
|
|