Mathématiques,
Brevet Nouvelle Calédonie 02 /2020.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
..
..
|
|
......
.....
|
Exercice 1 (16
points)
Pour chacune des affirmations suivantes, indiquer sur la copie, si elle
est vraie ou fausse.
On rappelle que chaque réponse doit être justifiée.
La fonction f est définie par f(x)=2(x-3).
• Affirmation n° 1 :
L'image de 5 par la fonction f est 4. Vrai.
f(5) =2(5-3) = 2 * 2 = 4.
Le parc éolien de prony est composé de 84 éoliennes. Chaque éolienne produit en moyenne 256 000 watts.
• Affirmation n° 2 :
Le parc éolien produit au total environ 21,5 mégawatts. Vrai.
256 000 W = 0,256 MW ; 84 x 0,256 ~21,5 MW.
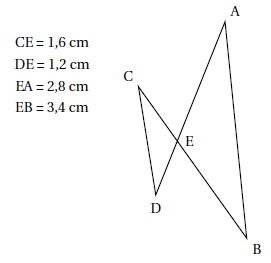
• Affirmation n° 3 : Les droites (AB) et (CD) sont parallèles. Faux.
EB / EC =3,4 / 1,6 =2,125 ; EA / ED =2,8 / 1,2 ~2,333.
EB / EC diffère de EA / ED, les droites (AB) et (CD) ne sont pas parallèles.
Le pentagone ci-dessous est composé de 5 triangles.
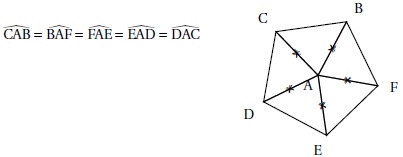
• Affirmation n° 4 : L'angle de rotation de centre A qui transforme C en D dans le sens des aiguilles d'une montre est 60°. Faux.
360 / 5 * 4 =288 °.
Exercice 2. 12 points
Laura a créé trois variables puis a réalisé le script ci-dessous.
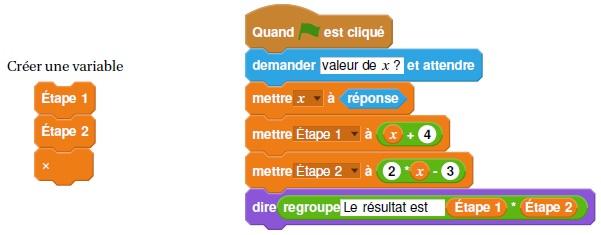
1. Vérifier que si la valeur de x est 5 alors le résultat est 63.
5+4=9 ; 2*5-3=7 ; 9 * 7 =63.
2. Quel résultat obtient-on si la valeur de x est -3 ?
-3+4 = 1 ; 2*(-3)-3= -9 ; 1 *(-9) = -9.
3. Parmi les expressions suivantes, quelle est celle qui correspond au programme de calcul donné par le script ?
(x+4)(2x-3) vrai ; x+4*2x-3 ; x+4*(2x-3).
4. Pour quelle(s) valeur(s) de x obtient-on la valeur zéro ?
x+4=0 ; x = -4 et 2x-3=0 soit x = 1,5.
|
| .
. |
.
.
|
Question 3. (16
points)
Un aquaculteur étudie l'évolution de la masse moyenne de crevettes dans
un bassin. Il dispose de valeurs théoriques. Répondre aux questions à
partir du graphe.
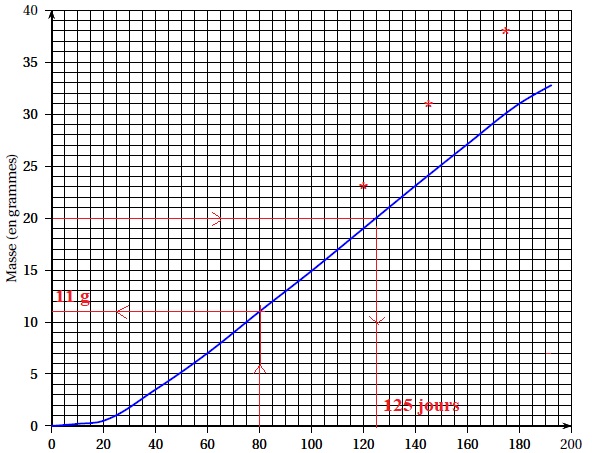
1. a. La masse moyenne théorique des crevettes est-elle proportionnelle au nombre de jours passés dans le bassin ?
Non, le graphe n'est pas une droite passant par l'origine.
1.b. Au bout de 80 jours, quelle est la masse moyenne théorique des crevettes ? 11 g.
1.c.
La pêche dans le bassin pourra être effectuée lorsque la masse moyenne
des crevettes atteint 20 g. Au bout de combien de jours peut-on
envisager la pêche ? 125 jours.
2. L'aquaculteur effectue régulièrement des relevés dans son bassin.
Nombre de jours
|
120
|
145
|
175
|
Masse moyenne relevée ( g)
|
23
|
31
|
38
|
Placer ces points sur le graphique.
Comparer les masse moyennes relevées par rapport aux masses moyennes théoriques.
Les masse moyennes relevées sont supérieures aux masses moyennes théoriques.
Exercice 4.
(12
points).
Les
crevettes mangent des granulés stockés dans des silos. Un silo est
composé d'un cône de révolution surmonté d'un cylindre de même base de
diamètre D=2 RC = 2,8 m. La hauteur du cylindre est h =2,4 m.
1. Calculer le volume du cylindre.
p R2h =3,14 x 1,42 x2,4 =14,778 ~15 m3.
2. Montrer que la hauteur AB du cône est environ de 2,5 m.
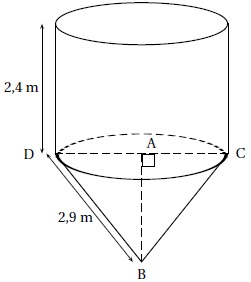
BD2=AD2 +AB2 ; AB2 = BD2-AD2 =2,92-1,42=6,45 ; AB ~2,5 m.
3. Calculer le volume du silo.
Volume du cône : p R2 AB / 3 = 3,14 x 1,42 x 2,5 / 3 ~5 m3.
Volume du silo : 15 +5 = 20 m3.
4. L'aquaculteur commande 16 m3 de granulés de masse volumique 750 kg / m3. Prix du kg : 160 F CFP.
Calculer le montant total de la commande.
Masse : 16 x 750 =12 000 kg.
Montant de la commande : 12 000 x 160 =1 920 000 F CFP.
|
. .
|
Exercice 5.
(12 points)
L'image satellite suivante représente 6 bassins de forme rectangulaire.
1. Estimer la longueur et la largeur d'un bassin.

2. On considère un bassin dont la surface est 4500 m2. Chaque bassin reçoit 2 larves de crevettes par m2. Quelle quantité de larves faut-il prévoir pour 6 bassins.
2 x 4500 x 6 =54 000.
3. Toutes les
larves ne survivent pas lors du transfert en bassin. Il faut prévoir de
commander 10 % de larves supplémentaires pour 6 bassins. Quelle
quantité totale de larves faut-il commander ?
54 000 x 1,1 =59 400.
Question 6. (12
points)
Partie A.
Dans un bassin, l'aquaculteur relève la masse de 100 crevettes.
|
A
|
B
|
C
|
D
|
E
|
F
|
G
|
H
|
I
|
1
|
Masse (g)
|
18
|
19
|
21
|
23
|
25
|
26
|
28
|
|
2
|
Effectif |
7
|
12
|
19
|
25
|
14
|
13
|
10
|
|
1. Dans la cellule I2 on saisit la formule = SOMME(B2:H2). Quelle nombre s'affiche dans cette cellule ?
7+12+19+25+11+14+13+10=100
2. On choisit au hasard une crevette. Toutes les crevettes ont la même probabilité d'être choisie.
a. Quelle est la probabilité que la masse de la crevette soit de 21 g ?
19 / 100=0,19.
b. Quelle est la probabilité que la masse de la crevette soit supérieure ou égale à 25 g ?
(25 +14 +13 +10) / 100 =0,62.
Partie B.
Lors de la pèche on relève la masse (g) de quelques crevettes :
20 ; 18 ; 17 ; 28 ; 28 ; 22 ; 24 ; 24 ; 22 ; 24.
1. Calculer la moyenne de cette série.
(20 +18 +17 +28 +28 +22 +24 +24 +22 +24) / 10 =22,7 g.
2. Calculer la médiane de cette série et interpréter.
Ordonner les valeurs : 17 ; 18 ; 20 ; 22 ; 22 ; 24 ; 24 ; 24 ; 28 ; 28.
La médiane est comprise entre 22 et 24 g, par exemple 23 g.
La moitié des crevettes ont une masse inférieure à 23 g ; la moitié des crevettes ont une masse supérieure à 23 g.
|
Exercice 7. (10 points)
On
a schématisé ci dessous, un bassin d'aquaculture par vue de côté. Le
fond du bassin représenté par le segment [EB] doit être en pente.
Le bassin est bien construit quand l'angle a est compris entre 0,1° et 0,2°.
CE = 2,8 m ; BD=CA=3,2 m et AB = 150 m. Ce bassin est-il bien construit ? Justifier.
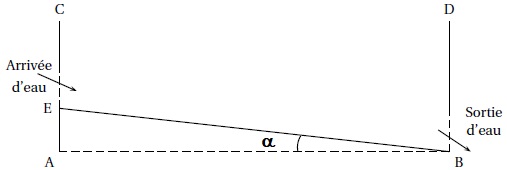
AE = AC-CE = 3,2-2,8 = 0,4 m.
tan a = AE / AB = 0,4 / 150 ~0,00267 ; a = 0,15 °, valeur comprise entre 0,1 et 0,2 °.
Le bassin est bien construit.
Exercice 8. (10 points).
On souhaite représenter 6 bassins rectangulaires à l'aide d'un logiciel de programmation.
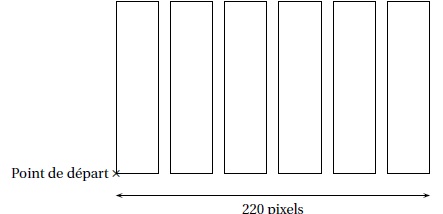
1. Compléter le
script du bloc "bassin" pour qu'il permette de tracer un bassin
rectangulaire de largeur 30 pixels et de longueur 150 pixels.
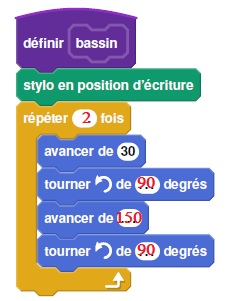
2. Le script ci-dessous permet d'obtenir la figure ci-dessus. Il utilise le bloc "bassin".
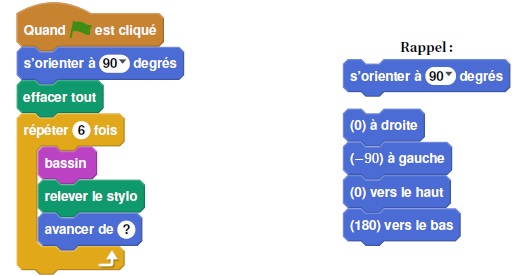
Quelle valeur doit être placée à la dernière ligne dans la consigne "avancer" ? Justifier.
On note y l'intervalle en pixels entre deux ractangles.
220 = 6 x30 + 5 y ; 40 = 5 y ; y =8.
"avancer de 38".
|
|
|









