Mathématiques,
Brevet Nouvelle Calédonie 12 /2020.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
..
..
|
|
......
.....
|
Exercice 1 QCM (18
points)
1. 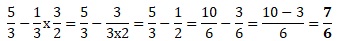 Réponse C. Réponse C.
2. L'écriture scientifique de 245 10-5 est : 245 x5 ; 2,45 10-3 vrai ; 2,45 107.
3.4. On donne les durées en minutes entre les différents arrêts d'une ligne de bus :
3 ; 2 ; 4 ; 3 ; 7 ; 9 ; 7.
La durée moyenne est : 3 min ; 4 min ; 5 min.
(3+2+4+3+7+9+7) / 7=5 min.
La durée médiane est : 3 min ; 4 min ; 5 min.
Ranger par ordre croissant : 2 ; 3 ; 3 ; 4 ; 7 ; 7 ; 9. La médiane est la quatrième valeur.
5. Un jeu de 32 cartes compte 4 rois. On tire au hasard une carte. Quelle est la probabilité d'obtenir un roi ?
1 /8 ; 1 /32 ; 3 / 32.
4 cas favorables sur 32 cas possibles. La probabilité de tirer un roi est 4 / 32 = 1 /8.
6. Une ville située sur l'équateur peut avoir pour coordonnées : (45°N ; 45° E) ; (78°N ; 0° E) ; (0°N ; 78° O).
Exercice 2. 8
points
Un prix TTC s'obtient en ajoutant la taxe TGC au prix HT.
En Nlle Calédonie, il existe 4 taux de TGC selon les cas : 22 % ; 11% ; 6 % et 3 %.
Alexis vient de faire réparer sa voiture chez un carrossier. On donne
un extrait de la facture. Les colonnes B, D et E désignent les prix en
francs.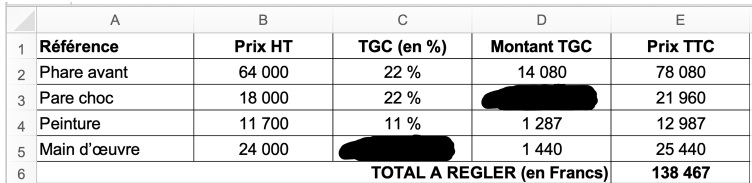
1. Quel est le montant TGC pour le pare choc ?
18 000 x 0,22 =3960 ou 21960-18 000 = 3 960.
2. Quel est le pourcentage de TGC qui s'applique à la main d'oeuvre ?
1440 / 24 000 =0,06 ( 6%).
3. Quelle formule a été saisie dans la cellule E6 pour obtenir le total à payer ?
=SOMME(E2: E5)
Exercice 3. (11
points)
On donne deux programme de calcul suivants :
A : choisir un nombre ;
soustraire 5 à ce nombre ;
multiplier le résultat par le nombre de départ.
B : choisir un nombre ;
mettre ce nombre au carré ;
soustraire 4 au résultat.
1. Alice choisit le nombre 4 et applique le programme A. Montrer qu'elle obtient -4.
4-5 = -1 ; -1 x 4 = -4.
2. Lucie choisit le nombre -3 et applique le programme B. Quel résultat va t-elle obtenir ?
(-3)2-4 = 9-4 = 5.
Tom souhaite trouver un nombre pour lequel les deux programmes donnent le même résultat.Il choisit x.
3. Montrer que le résultat du programme A peut s'écrire : x2-5x.
(x-5) x = x2-5x
4. Exprimer en fonction de s le résultat du programme B.
x2-4.
5. Quel est le nombre que TOM cherche ?
x2-5x = x2-4 ; 5x = 4 ; x = 4 /5 =0,8.
|
| .
. |
.
.
|
Exercice 4.
(16
points).
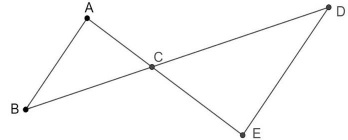
On donne les distances en mètres. AB = 400 ; AC = 300 ; BC = 500 ; CD = 700.
Les droites (AB) et (DE) sont parallèles
1. Calculer la longueur DE.
Les triangles ABC et CDE sont semblables.
DE / AB = CD / BC =700 / 500 = 7 /5 =1,4 ; DE = 1,4 AB = 1,4 *400=560.
2. Montrer que le triangle ABC est rectange.
BC2=5002=250 000.
AC2 +AB2 =3002+4002=250 000.
D'après la réciproque du théorème de Pythagore, le triangle ABC est rectangle en A.
3.
Calculer la mesure de l'angle ABC.
tan (ABC) = AC / AB = 300 / 400 = 0,75 ; l'angle ABC mesure environ 37°.
Lors
d'une course les concurrents doivent effectuer plusieurs tours du
parcours représentés ci-dessus. Ils partent du point A, puis passent
par les points B, C, D et E dans cet ordre puis de nouveau par le point
C pour revenir en A.
Le vainqueur a mis 1 h 48 min pour effectuer 5 tours du parcours. La distance parcourue pour faire un tour est de 2880 m.
4. Calculer la distance totale parcourue.
2880 x 5 = 14 400 m.
5. Calculer la vitesse moyenne du vainqueur.
48 / 60 = 0,8 ; 1 h 48 min = 1,8 heures.
14 400 / 1,8 = 8000 m /h = 8 km / h.
|
. .
|
Exercice 5.
(7 points)
Un triangle ABC rectangle en B est tel que AB = 5 m et AC = 5,25 m.
1. Calculer BC.
AC2 = AB2 +BC2 ; BC2 = AC2 - AB2 =5,252-52=2,5625. BC =1,6 m.
Une corde non élastique de 10,5 m de long est fixée au sol par ses deux extrémités entre deux poteaux distants de 10 m.
2. Melvin qui mesure 1,55 m pourrait-il passer sous cette corde sans se baisser en la soulevant par la milieu ?
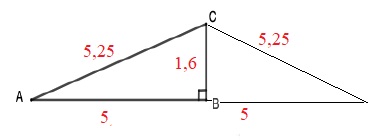
D'après le calcul précédent BC = 1,60 > 1,55. Melvin peut passer.
Question 6. (14
points)
1. Justifier que 102 est divisible par 3.
La somme des chiffres de 102 est égale à 3 ; 102 est donc divisible par 3.
2. On donne la décomposition en facteurs premiers de 85 : 85 = 5 x 17.
Décomposer 102 en facteurs premiers.
102 = 2 x3 x17.
3. Donner 3 diviseurs non premiers de 102.
6 ; 34 ; 51.
Un
libraire dispose d'une feuille cartonnée de 85 cm x 102 cm. Il souhaite
découper dans celle-ci, en utilisant toute la feuille, des étiquettes
carrées. les côtés de ces étiquettes ont toutes la même mesure.
1. Les étiquettes peuvent-elles avoir 34 cm de côtés..
Non, car 34 n'est pas un diviseur de 85.
2. Le libraire découpe des étiquettes de 17 cm de côté. Combien d'étiquettes peut-il découper ?
Il peut découper 5 bandes de 17 cm sur la longueur et 6 bandes de 17 cm sur la largeur soit 6 x 5 = 30 étiquettes.
|
Exercice 7. (15 points)
Nolan souhaite construire une habitation. Il hésite entre une case et une maison.
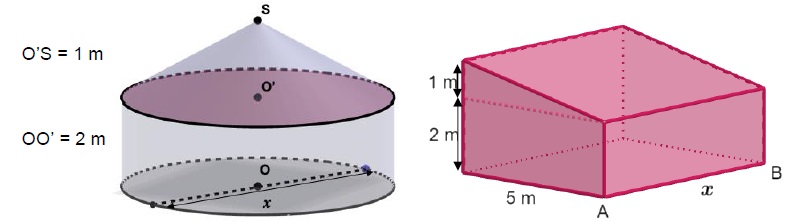
Partie 1. On considère que x = 6 m.
1. Montrer que le volume exact de la partie cylindrique de la case est 18 p m2.
Aire de base fois hauteur = p (0,5x)2 OO' = p x 32x 2 =18 p m2.
2. Calculer le volume de sa partie conique.
aire de base fois hauteur / 3 = p (0,5x)2 O'S / 3 = 3 p ~9,4 m3.
3. En déduire que le volume total est environ 66 m3.
18 x3,14 +9,4 ~ 66 m3.
Partie 2.
On a représenté la fonction qui donne le volume total de la case en fonction de son diamètre x.
1. Par lecture graphique, donner le volume d'une case de 7 m de diamètre.
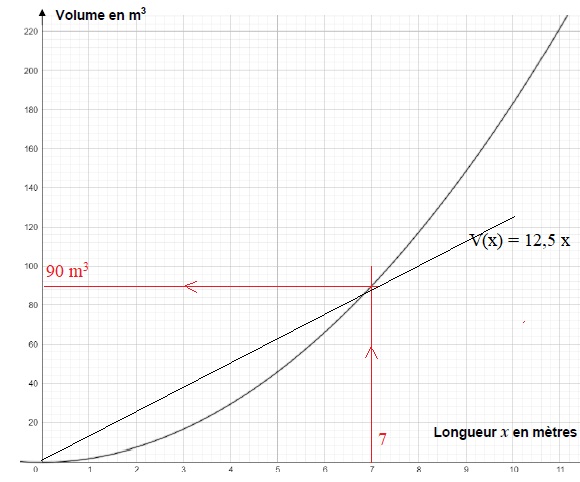
La fonction qui donne le volume de la maison en forme de prisme droit est V(x) = 1,25 x.
2. Calculer l'image de 8 par la fonction V..
V(8) = 12,5 * 8 = 100.
3. Quelle est la nature de la fonction V.
Fonction linéaire.
4. Tracer la représentation graphique de la gonction V.
Pour des raisons pratiques, la valeur maximale de x est de 6 m .
Nolan souhaite choisir la construction qui lui offrira le plus
grand volume.
5. Quelle construction va t-il choisir ? Justifier.
D'après le graphique, pour x compris entre 0 et 6 m, le volume de la
maison en forme de prisme possède un volume supérieur à celui de la
case.
Exercice 8. (11
points).
Le script suivant permet de tracer un carré de côté 50 unités.
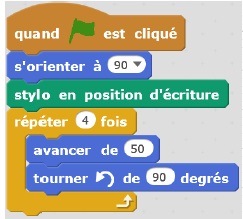
1. Compléter le
script suivant pour obtenir un triangle équilatéral de côté 80 unités.
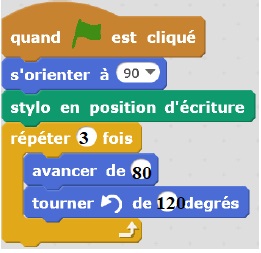
2. On a lancé le script suivant. Entourer la figure obtenue avec ce script.
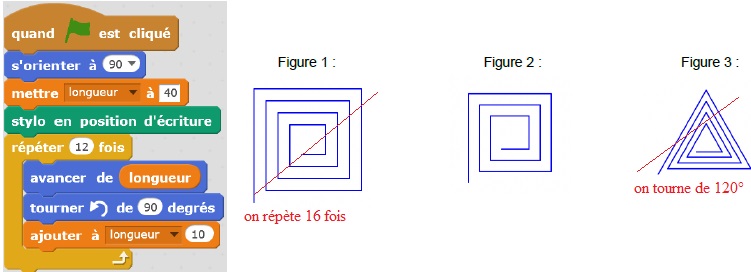
|
|
|