Math�matiques BTS groupe A M�tropole Antilles 05/21. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicit�s adapt�es � vos centres d’int�r�ts. .. .. . . .. .. ...... ... Exercice 1.(11 points). Le principe des CPL consiste � superposer au r�seau �lectrique un signal de haute fr�quence et de basse �nergie. Ce deuxi�me signal se propage sur l'installation �lectrique et peut �tre re�u et d�cod� � distance. A. Etude d'un signal. a. Quelle est la valeur de la p�riode T ? T = 10 �s = 1,0 10-5 s. b. Quelle est la fr�quence de cette tension ? f = 1 / T = 1 / 10-5 = 1,0 105 Hz. 2. On mod�lise l'�volution de U ( en V) � l'aide d'une fonction num�rique f  d�finie sur R . U(t) = f(t). f est paire, p�riodique de p�riode T, d�veloppable en s�rie de Fourier. 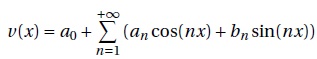a. Justifier que bn=0 pour tout entier n > 1. v est une fonction paire ; sin(nx) est une fonction impaire ; les termes sin(nx) sont donc nuls. b. Justifier que a0 = 9,6. 3. Montrer que Ueff = 10,7 V. 4. Le signal correspondant � la tension U est envoy� sur une ligne moyenne tension transportant une tension efficace  de M = 20 000 V. Le taux de distorsion harmonique par rapport au fondamental, not� TF est donn� par : TF2 = (Ueff2 -a02) / M2. On conssid�re qu'un CPL n'a pas d'incidence sur le r�seau si TF < 0,1 %. Le CPL �tudi� a t-il une incidence sur le r�seau ? TF2 = (10,72 -9,62) / (2 104)2=5,6 10-8 ; TF ~2,4 10-4 ( 2,4 10-2 %). Cette valeur �tant inf�rieure � 0,1 %, le CPL n'a pas d'incidence sur le r�seau. B. Transmission num�rique.  Le signal porteur �tudi� en A peut �tre utilis� pour transmettre des signaux num�riques (bits) durant chaque p�riode. Dans certaines conditions les bits peuvent �tre mal transmis. On se place dans cette partie, dans ces conditions. On transmet, durant chaque p�riode, 80 bits. Chaque bit a une probabilit� �gale � 0,015 d'�tre mal transmis. On note X la variable al�atoire qui associe � chaque p�riode le nombre de bits mal transmis durant cette p�riode. 1. Quelle est la loi de probabilit� suivie par X ? Pr�ciser ces param�tres. Loi binomiale de param�tres n = 80 et p = 0,015. 2. Calculer la probabilit� que tous les bits soient correctement transmis durant cette p�riode. P(X = 0)= 0,298. 3. Calculer la probabilit� que strictement plus de 4 bits soient mal transmis. P(X > 4) = 1-P(X < 4) =1-0,9928 ~7,2 10-3. 4.a. Calculer l'esp�rance de la variable X. E = n p = 80 x0,015=1,2. b. On consid�re que la ligne est de bonne qualit� si, en moyenne, moins de 2 bits sont mal transmis durant une p�riode. La ligne est-elle de bonne qualit� ? E = 1,2 < 2, la ligne est de bonne qualit�. C. Dur�e de vie d'un coupleur CPL. On mod�lise cette dur�e de vie par une variable al�atoire Y suivant une loi normale de moyenne 12 et d'�cart type s = 2. 1. Calculer la probabilit� qu'un coupleur ait une dur�e de vie comprise entre 10 et 12 ans. P(Y < 10) =0,15865 ; P(Y < 12) =0,500 ; P(10 < Y <12)=0,5-0,15865=0,341. 2. Calculer la probabilit� qu'un coupleur ait une dur�e de vie sup�rieure � 10 ans. P(Y > 10) = 1-P(Y <10) = 1-0,15865 ~0,841. 3. Sachant qu'un coupleur est toujours en fonctionnement au bout de 10 ans, calculer la probabilit� qu'il cesse de fonctionner dans les deux ann�es suivantes. PY >10 ( Y <12) = P(10 < Y <12) / P(Y > 10) ~0,341 / 0,841 ~0,406. ... .... Exercice 2. (9 points). Le montage suivant est constitu� d'une bobine d'inductance L = 0,001 H et d'une r�sistance R, assembl�es en s�rie.  Ce montage est utilis� pour extraire un signal CPL haute fr�quence du r�seau. A. Test du filtre. Dans cette partie, R est un param�tre strictement positif fix�. La tension ve est constante �gale � 12 V. A t=0, on admet que la tension aux bornes de la bobine est 12 V. La tension vs v�rifie pour tout t > 0 : v's +R/L vs =0. 1. D�terminer les solutions de l'�quation diff�rentielle. vs(t) = A exp(-R / L) t avec A une constante. 2. En d�duire que vs(t) = 12 exp(-1000 R t). A t=0 : vs(t=0) = 12 = A e0 = 12. R / L = R / 0,001 = 1000 R. vs(t) = 12 exp(-1000 R t). 3.a Quel est le sens de variation de la fonction vs ? Justifier. v's(t) = -12 000 R exp(-1000 R t) strictement n�gative. vs(t) est strictement d�croissante. b. D�terminer la limite de vs(t) quand t tend vers plus l'infini. Quand t tend vers plus l'infini, exp(-1000 R t). tend vers z�ro. vs(t)  tend donc vers z�ro. 4. D�terminer la valeur de R telle que pour t = 0,001, la tension vs(t) soit �gale � 1 % de la tension d'entr�e ve. vs(t=0,001)=0,12  = 12 exp(-1000 R *0,001). 0,01 = exp(-R) ; R = -ln(0,01) ~4,6 ohms. B . Etude du filtre. Fonction �chelon U(t) = 0 si t < 0 et U(t) = 1 si t > 0. On prendra R = 5 ohms. On admet que la fonction de transfert du montage est H(p) = p /(p +5000). 1. On consid�re que pour tout r�el t :  ve(t) = 12 U(t) -12 U(t-8 10-6).   D�terminer la valeur de ve(t) pour t < 0, puis pour  0 < t < 8 10-6  et enfin pour t > 8 10-6. t < 0 : U(t) = 0 et ve(t) =0. 0 < t < 8 10-6  : ve(t) = 12 . t > 8 10-6 :  ve(t) = 12  -12 =0. 2.a D�terminer la transform�e de Laplace VE(p) de ve(t). ve(t) = 12 U(t) -12 U(t-8 10-6). VE(p) = 12 / p -12 / p exp(-8 10-6p). b. En d�duire que VS(p) =12 /(p+5000) -12 exp(-8 10-6p) / (p+5000). VS(p) = H(p) x VE(p) = p /(p +5000) [12 / p -12 / p exp(-8 10-6p)]. VS(p) =12 / (p +5000) -12 / (p +5000) exp(-8 10-6p). 3. Exprimer vs(t) en fonction de t et de la fonction �chelon U. vs(t) =12 exp(-5 103t)U(t)-12exp(-5 103(t-8 10-6))U(t-8 10-6). . 4. On a repr�sent� la tension de sortie vs en fonction de t exprim� en microseconde. Sur le m�me graphique repr�senter la tension d'entr�e ve. Que constate t-on ? ve(t) et vs(t) ont quasiment les m�mes valeurs.

menu