Mathématiques
BTS groupe B 09/20.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
..
..
|
.
.
|
..
..
......
...
|
Exercice 1.
Un
jouet est un bonhomme de neige monté sur un ressort. On comprime le
jouet au sol et une fois relâché, celui-ci est propulsé dans les airs à
une certaine hauteur et retombe ensuite sur le sol. Le mouvement est
supposé vertical. On souhaite étudier la hauteur atteinte en fonction
du nombre d'années d'utilisation. La hauteur atteinte est modélisée par
une solution de l'équation différentielle (E) :
y" +2y'+y = 3.
y est une fonction de la variable x, durée d'utilisation en années.
A. Résolution de l'équation différentielle.
1. Résoudre dans R, l'équation y" +2y'+y=0.
Equation caractéristique : r2 +2r +1 =0.
Discriminant D = 22-4 x1 = 0 ; solution unique r =(-2+0) / 2 = -1.
f(x) = (Ax +B) e-x avec A et B des constantes réelles.
2. Déterminer la valeur de k, constante réelle, pour que la fonction g(x) = k soit solution de (E).
g'(x) = g"(x) = 0 ; k = 3.
3. En déduire les solutions de (E).
f(x) = (Ax +B) e-x +3.
4. Déterminer la fonction f, solution de (E) telle que f(0) = 4 et f(2) = 5e-2+3.
f(0)=4 =B+3 ; B = 1.
f(2) =(2A+1) e-2+3 =5e-2+3.
(2A+1) e-2 =5e-2 ; 2A+1 = 5 ; A = 2.
f(x) = (2x +1) e-x +3.
B. Etude de la fonction f.
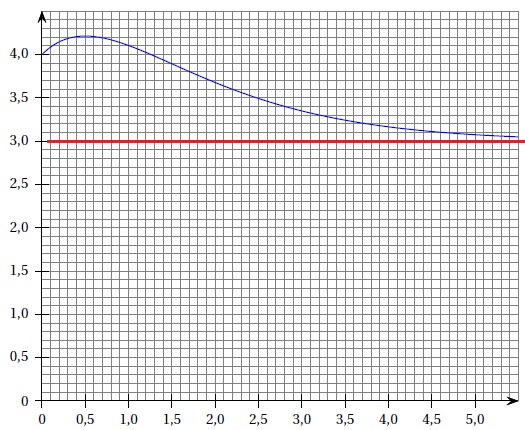
On note C la courbe représentative de f.
1. Quelle hauteur peut atteindre le jouet lors de la premmière utilisation ?
x = 0 ; f(0) =4 dm.
2. Quelle hauteur peut atteindre le jouet après 6 mois d'utilisation ?
x = 0,5 ; f(0,5) = 2e-0,5 +3 ~4,21 dm.
3. On admet que la limite en plus l'infini de x e-x = 0.
a. Déterminer la limite de f en plus l'infini.
f(x) = 2xe-x +e-x+3.
En plus l'infini : limite de 2xe-x = 0 ; limite de e-x = 0 ; limite de f(x) = 3.
b. En déduire que la courbe C admet une asymptote D. Tracer cette droite. Interpréter.
La courbe C admet une asymptote d'équation y = 3. La hauteur maximale atteinte au bout d'un grand nombre d'années est 3 dm.
4.a Justifier que f '(x) = (1-2x)e-x.
On pose u = 2x+1 et v =e-x ; u' = 2 ; v' = -e-x.
u'v +v'u =2e-x -(2x+1)e-x =(1-2x)e-x.
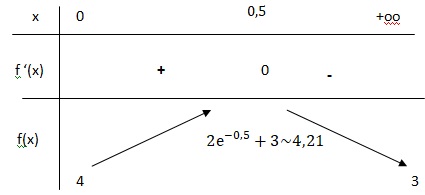
b. Etudier le signe de f '(x) et en déduire le tableau de variation de f.
e-x >0 ; f '(x) a le signe de 1-2x.
f '(x) = 0 pour x = 0,5 ; f '(x) > 0 pour x appartenent à [0 ; 0,5] et f '(x) < 0 pour x > 0,5.
5. On admet que F(x) = (-2x-3)e-x
+3x est une primitive de la fonction f. Calculer l'aire du plan
comprise entre la courbe C, l'axe des abscisses et les droites
d'équation x = 0 et x = 2.
A = F(2) -F(0) = - 7e-2 +6 + 3=9-7e-2 ~8,05 unités d'aire soit 8,05 x4 =32,21 cm2.
|
...
|
....
|
Exercice 2. Groupe B1.
Des billes doivent avoir un diamètre de 12,7 mm.
A. Loi normale.
On note X une variable aléatoire qui, à chaque bille
associe son diamètre en mm. X suit la loi normale de moyenne µ=12,7 et
d'écart type s.
1. QCM. On admet que P(12,6 < X <12,8)~0,95.
La valeur de l'écart type est : 0,05 vrai ; 0,1 ; 0,15 ; 0,2.
95 % : les observations sont comprises dans l'intervalle [µ-2s ; µ+2s].
2.
Donner la probabilité, arrondie au centième, qu'une bille prélevée au
hasard dans la production ait un diamètre strictement supérieur à 12,8
mm.
P(X >12,8) = 1-P(X < 12,8 )= 1-0,9772 ~0,02.
B. Probabilités conditionnelles.
L'équipementier propose ses billes en céramiques plus légères à deux
marques automobiles A et B. On choisit au hasard une bille dans la
production.
La probabilité que la bille soit achetée par la marque A est 0,3. La probabilité qu'elle soit achetée par la marque B est 0,7.
Sachant qu'elle a été achetée par la marque A, la probabilité que la
bille soit utilisée dans le roulement d'un nouveau prototype est 0,75.
On note les événements :
A : la bille est achetée par la marque A.
B : la bille est achetée par la marque B.
R : la bille est utilisée dans le roulement d'un nouveau prototype.
1.a. Donner la valeur de PA(R)
0,75.
1.b. Démontrer que P(A n R) = 0,225.
P(A n R) =P(A) x PA(R) =0,3 x0,75 =0,225.
2. On admet que P(R) = 0,9.
a. Justifier que P(B n R) = 0,675.
Formule des probabilités totales : P(R) = P(A n R) + P(B n R).
P(B n R) =0,9 -0,225 =0,675.
b. En déduire la valeur arrondie au centième de PB(R).
PB(R) = P(B n R) / P(R) =0,675 /0,9~0,75.
3. Calculer la probabilité qu'une bille ait été achetée par la marque A sachant qu'elle est utilisée dans un nouveau prototype.
PR(A) =P(R n A) / P(R) =0,225 / 0,9 =0,25.
C . Test d'hypothèse au seuil de 5 %.
On
note Y la variable aléatoire qui à chaque bille produite associe son
diamètre en mm. Y suit la loi normale de moyenne µ et d'écart type s = 0,045.
On prélève au hasard un échantillon de 200 billes dans la production. L'hypothèse H0 est µ =12,7. L'hypothèse H1 est µ diffère de 12,7.
1.a. Sous l'hypothèse H0, justifier que la variable aléatoire 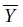 suit la loi normale de paramètres 12,7 et d'écazrt type 0,003. suit la loi normale de paramètres 12,7 et d'écazrt type 0,003.
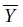 suit la loi normale de paramètres 12,7 et d'écart type s / n½ =0,045 / 200½ = 0,045 / 14,14 ~0,003. suit la loi normale de paramètres 12,7 et d'écart type s / n½ =0,045 / 200½ = 0,045 / 14,14 ~0,003.
b. Calculer la valeur du réel h, tel que sous l'hypothèse H0, on ait : P(12,7 -h < 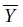 < 12,7 +h) =0,95.. < 12,7 +h) =0,95..
h = 1,96 s =1,96 x 0,003 ~0,006.
2. Enoncer la règle de décision du test.
Intervalle de confiance :[12,7-0,006 ; 12,7 +0,006) soit [12,694 ; 12,706].
Si la moyenne appartient à cet intervalle, H0 est valide, sinon H1 est valide.
3.
Sur un échantillon de 200 billes prélevé au hasard dans la production,
on a relevé un diamètre moyen de 12,71 mm. L'équipementier peut-il
remettre en cause le diamètre annoncé de billes ? Justifier.
12,71 n'appartient pas à l'intervalle [12,694 ; 12,706] ; l'hypothèse H0 est rejetée, H1 est valide. Le diamètre moyen des pièces est remis en cause.
Exercice 2. Groupe B2.
La fonction échelon unité U est définie par : U(t) = 0 si t < 0 et U(t) = 1 si t > 0.
On considère un système électrique entrée-sortie. On note s le signal
de sortie associé au signal d'entrée e. Les foncations e et s
sont nules pour t < 0. On admet que le fonctions e et s admettent
des transformées de Laplace notées respectivement E et S. La fonction
de transfert H du système est définie par S(p) = H(p) x E(p).
On considère le signal d'entrée e défini sur R par e(t) = U(t)-2U(t-1)
et la fonction H définie sur ]0 ; +oo[ par H(p) = 1 / (p+1).
1.a. Calculer e(0,5) et e(2).
e(0,5) = U(0,5)-2U(-0,5).
U(-0,5) = 0 ; U(0,5) = 1 ; e(0,5) = 1.
e(2) = U(2)-2U(1).
U(2) = 1 ; U(1) = 1 ; e(2) = 1-2 = -1.
b. Tracer la courbe représentative de la fonction e. On pourra calculer e(-0,5), e(0), e(0,9), e(1).
e(-0,5) =U(-0,5)-2U(-1,5) = 0.
e(0) =U(0)-2U(-1) = 1.
e(0,9) =U(0,9)-2U(-0,1) = 1.
e(1) =U(1)-2U(0) = -1.
Si t < 0, e(t) = 0 ; si 0 < t < 1 ; e(t) = 1 ; si t > 1, e(t) = -1.
2. Pour tout p > 0, déterminer E(p), E étant la transformée de Laplace du signal e.
Si 0 < t < 1 ; e(t) = 1 :
E(p) = 1 / p.
Si t > 1, e(t) = -1 :
E(p) = -1 / p.
3.a. Donner l'expression de S(p).
S(p) = H(p) x E(p) =1 / (p+1)E(p).
Si 0 < t < 1 ; S(p) =1 / [p(p+1)].
Si t > 1; S(p) = -1 / [p(p+1)].
b. Vérifier que pour tout t >0 : 1 / [p(p+1)] = 1 /p -1 /(p+1).
1 /p -1 /(p+1) =( p+1-p) / [p(p+1)] = 1 / [p(p+1)].
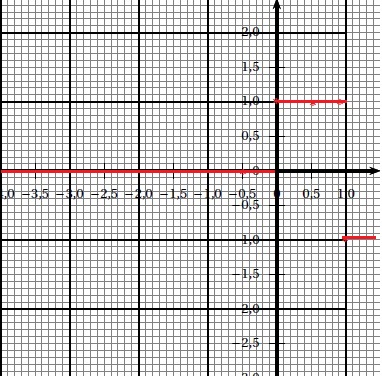
c. Justifier alors que pour tout p >0 : S(p) =1/p-1/(p+1) -2e-p / p+2e-(p+1)/(p+1).
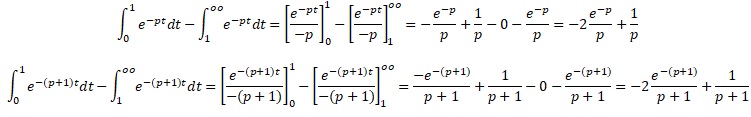
4. Compléter le tableau suivant et en déduire l'expression de s(t) sur [0 ; 1[.
Transformée
|
1 /p
|
1 / (p+1)
|
e-p / p
|
e-p / (p+1) |
Original
|
1
|
e-t
|
e-t(t-0) U(t-1) |
e-t(t-1) U(t-1)
|
5. On admet que l'expression de s sur [1 ; +oo[ est s(t) = (2e1)e-t-1.
a. Calculer s(1).
s(1) =2e1 *e-1-1 = 1
b. Compléter la courbe représentative de s(t).
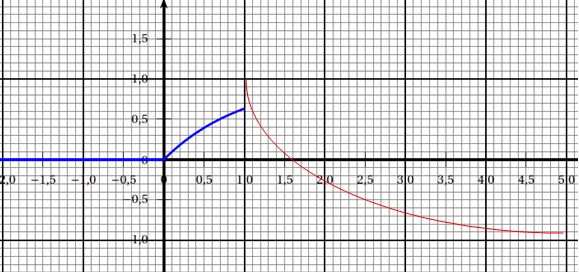
c. Donner la limite de la fonction s en plus l'infini.
e-t tend vers zéro et s(t) tend ves -1.
|
|