Mathématiques BTS groupe B1 Métropole Antilles Polynésie 05/21.

Mathématiques BTS groupe B1 Métropole Antilles Polynésie 05/21.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

.. ..

.
.

.. ..
......

...
Exercice 1.(10 points).
On note f(t) la hauteur en mètre du centre de gravité de l'hélicoptère par rapport au sol à l'instant t, exprimé en seconde..
A. Equation différentielle.
La fonction f est solution de l'équation différentielle (E) : y" +3y'+2y=4
1.a. Résoudre dans R l'équation r²+3r+2=0.
Discriminant D = 3²-4 x2 = 1.
Solutions : r₁ = (-3+1) / 2 = -1 ; r₂ =(-3-1) / 2 = -2.
b. En déduire les solutions de l'équation différentielle y" +3y'+2y=0.
f(t) = A e^-t +Be^-2t, avec A et B des constantes.
2. Soit k un nombre réel. On définit la fonction constante g sur [0 ; +oo[ par g(t) = k.
Déterminer k pour que g(t) soit solution de (E).
g' = 0 ; g" = 0 ; repport dans (E) : 2k = 4 ; k = 2.
3. En déduire l'ensemble des solutions de (E).
f(t) = A e^-t +Be^-2t+2.

B Etude de la fonction f.
On admet que la fonction f correspondant à la hauteur du centre de gravité de l'hélicoptère est définie sur [0 ; +oo[ par :
f(t) = - e^-t +1,5e^-2t+2.
On donne sa courbe représentative.

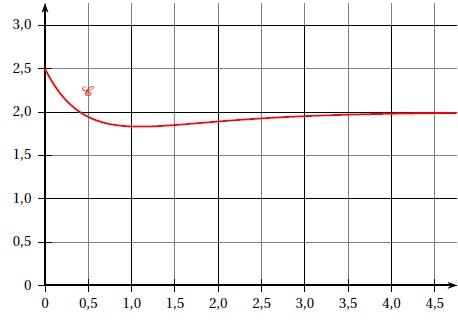
1. Déterminer la hauteur du centre de gravité de l'hélicoptère au moment de l'atterissage à t = 0.
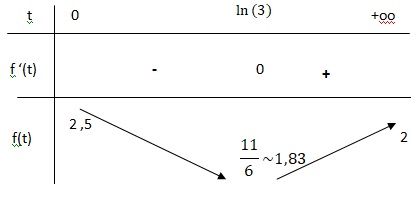
f(0) = - e^-0 +1,5e^-0+2= -1+1,5 +2 = 2,5 m.
2.a. Calculer la limite de f(t) en plus l'infini.
Les exponentielles tendent vers zéro en plus l'infini et f(t) tend vers 2.
b. En déduire que la courbe admet une asymptote dont on donnera son équation.
En plus l'infini la courbe est confondue avec la droite asymptote d'équation y = 2.
3.a A l'aide du graphique, conjecturer le sens de variation de la fonction f.
Sur [0 ; 1] la fonction est décroissante.
Sur [1 ; +oo[ la fonction est croissante.
b. On donne f '(t) = e^-t -3e^-2t.
Montrer que f '(t) peut s'écrire sous la forme f '(t) = e^-2t(e^t-3).
f '(t) = e^-2t+t -3e^-2t=e^-2t x e^t-3e^-2t=e^-2t(e^t-3).
c. Résoudre sur [0 ; +oo[ l'inéquation e^t-3 >0.
e^t >3 ; t > ln(3).
d. En déduire le signe de f '(t).
e^-2t est toujours positif. Le signe de f '(t) est celui de e^t-3.
Si t > ln(3), f '(t) est positive ; si t appartient à [0 ; ln(3)], f '(t) est négative.
e. Dresser le tableau de variation de la fonction f.

C. Etude locale.
Un logiciel donne la partie régulière du développement limité à l'ordre 2 de la fonction f au voisinage de zéro.
2,5 -2t +2,5t².
1.a Le développement limité de la fonction f au voisinage de zéro est :
2,5 -2t +2,5t² ; faux
2,5 -2t +2,5t²+t²e(t), avec e(t) tend vers zéro quant t tend vers +oo ; faux
2,5 -2t +2,5t²+t²e(t), avec e(t) tend vers zéro quant t tend vers zéro. Vrai.

1.b. Une équation de la tangente T à la courbe au point d'abscisse zéro est :
y=2,5 ; faux.
y = 2,5 -2t ; vrai.
y=2,5 -2t +2,5t²; faux.
2. Etudier la position relative de la courbe C et de la tangente T au voisinage de zéro.
f(t) -y =2,5 -2t +2,5t²-( 2,5 -2t )= 2,5t² >0.
T est en dessous de C.

...

....

Exercice 2. (10 points).
A. Loi binomiale.
La probabilité qu'une voiture prélevée au hasard parmi les garages d'une ensigne automobile soit réparée le jour même de sa réception est 0,7.
On interroge 100 clients de cette enseigne. On note X la variable aléatoire qui, à chaque échantillon de 100 clients interrogés, associe le nombre de clients dont le véhicule est réparé le jour même.
1. Justifier que X suit une loi binomiale dont on précisera les paramètres.
On interoge 100 clients de manière indépendante. Deux issues sont possibles " voiture réparée le jour même " ou" voiture non réparée".
On répète 100 fois une épreuve de Bernoulli.
X suit une loi binomiale de paramètre n =100 ; p = 0,7.
2. Calculer l'espérance de X et interpréter.
E = np = 70 ; en moyenne sur100 voitures, 70 sont réparées le jour même.
3. Calculer l'écart type de la variable X.
s = (np(1-p)^½ =(100 x 0,7 x0,3)^½ ~4,6.
4. Calculer la probabilité que, sur un échantillon de 100 clients, exactement 60 clients récupèrent leur voiture réparée le jour même.
P(X = 60) =C₁₀₀⁶⁰ x0,7⁶⁰ x0,3⁴⁰ ~0,00849 ~0,008.

B . Approximation par une loi normale de moyenne 70 et d'écart type 4,6.
On note Y la variable aléatoire de loi normale N(70 ; 4,6).
1. Calculer la probabilité qu'au moins 80 voitures sur un échantillon de 100 soient réparées le jour même.
P (Y > 79,5)=1 - P(Y < 79,5) = 1-0,9805 ~0,019.
2. Calculer la probabilité que le nombre de voitures sur un échantillon de 100, réparées le jour même soit compris entre 60 et 80.
P(Y < 59,5) =0,01123 ; P(Y < 80,5) =0,9888 ; P(59,5 < Y < 80,5) =0,9888-0,01123 =0,978.

C. Probabilités conditionnelles.
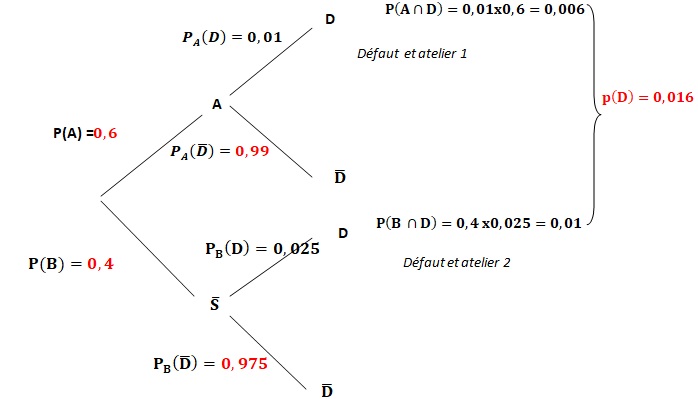
Un garage de cet enseigne possède deux ateliers. Les véhicules sont traités soit par l'atelier 1, soit par l'atelier 2.
1 répare 60 % des véhicules et le reste est réparé par l'atelier 2.
1 % des véhicules réparées par 1 présente un défaut de réparation ; 2,5 % des véhicules réparées par 2 présente un défaut de réparation.
On prélève au hasard un véhicule réparé par ce garage.
On définit les événements suivants :
A : "véhicule réparé par l'atelier 1".
B : "véhicule réparé par l'atelier 2".
D : " défaut de réparation sur le véhicule"
1. En déduire P(A), P(B), P_A(D) et P_B(D).
2. Calculer P(A n D) et P(B n D).
Calculer la probabilité qu'un véhicule présente un défaut de réparation.

D. Intervalle de confiance.
L'enseigne organise une enquète de satisfaction. Elle interroge 100 clients.
Soit F la variable aléatoire qui a tout échantillon associe la fréquence dans cet échantillon de clients satisfaits.
F suit la loi normale N(n ; p).
Pour l'échantillon prélevé, on constate que 87 clients sont satisfaits.
1. Donner une estimation de la proportion inconnue p.
p = 0,87.
2. Déterminer un intervalle de confiance centré sur f de la proportion p avec un coefficient de confiance de 95 %.
1,96 ( p(1-p) / 100)^½ =1,96 x(0,87 x0,13 /100)^½=0,066.
Intervalle de confiance : [0,87-0,066 ; 0,87 +0,066) soit [ 0,804 ; .0,936 ]

menu