Mathématiques
BTS groupe D2 Métropole Antilles Polynésie 05/21.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
..
..
|
.
.
|
..
..
......
...
|
Exercice 1.(10 points).
Une
usine produit de la viande hachée. On souhaite évaluer la durée de
conservation de cette viande hachée dans une chambre froide à 0°C.
Partie A.
Voici le relevé du nombre de germes putréfiants par cm2 tous les 5 jours à la surface d'un échantillon de viande hachée conservée dans la chambre froide.
1. Compléter la troisième ligne du tableau.
Nombre de jours de conservation ti
|
0
|
5
|
10
|
15
|
20
|
Nombre de germes par cm2 Ni
|
1000
|
4000
|
199 000
|
5 960 000
|
48 600 000
|
zi = ln(Ni)
|
6,91
|
8,29
|
12,20
|
15,60
|
17,70
|
2. Déterminer une équation de la droite d'ajustement du nuage de points Mi(ti, zi).
z = 0,58 t +6,36.
3. Placer les points sur le graphique et tracer la droite d'équation z = 0,6 t+6,4.
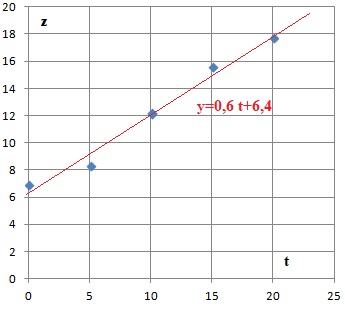
4. Cette droite est un ajustement du nuage de points ; ce modèle reste valable jusqu'au 30è jour de conservation. Donner une estimation du nombre de germes putréfiants par cm2 pour un stockage de 25 jours.
z = 0,6 x 25 +6,4 =21,4 ; N = e21,4 ~ 1,967 109= 1967 millions.
B. Etude de la fonction f(t) =600e0,6t sur [0 ; +oo[.
On admet que la fonction f modélise le nombre de germes par cm2 sur la surface de la viande conservée en chambre froide
1. Déterminer la limite de f en plus l'infini et interpréter.
Quand t tend vers plus l'infini, f(t) tend vers plus l'infini.
Le nombre de germes augmente au cours du temps et devient très grand.
2 Calculer la dérivée f '(t).
f '(t) = 600 x0,6e0,6t =360e0,6t.
3. En déduire le sens de variation de la fonction f(t).
La dérivée est strictement positive et la fonction f(t) est strictement croissante. Le nombre de germes croît indéfiniment..
4.a On définit le réel m de la façon suivante :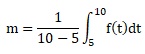
Sans calculer m, interpréter sa valeur.
m = nombre moyen de germes par cm2 entre le 5è et le 10è jour de conservation.
b. Donner une primitive de la fonction f.
F =600 / 0,6e0,6t = 1000 e0,6t.
c. En déduire que m = 200e6-200e3.
m = 1 /5 [1000 e0,6x10-1000 e0,6 x5]=200e6-200e3.
5.
On admet que la viande hachée peut être commercialisée si, lorsqu'elle
quitte l'usine, la concentration de germes à sa surface est strictement
inférieure à 3000 germes par cm2.
a. Résoudre l'inéquation f(t) < 3000.
600e0,6t < 3000 ; e0,6t < 5 ; 0,6 t < ln(5) ; t < ln(5) / 0,6 ( ~2,7)
b. En déduire si l'usine peut conserver la viande hachée plus de 2 jours avant la commercialiser.
Oui car le nombre de germes dépasse 3000 par cm2 au bout de 2,7 jours.
6. La viande peut être vendue à des particuliers tant que le nombre de germes par cm2 ne dépasse pas 27 000.
a. Donner la valeur numérique donnée par l'algorithme suivant en justifiant.
J=0
N=600
Tant que N < 27 000
J = J+1
N=600*e0,6*J
Fin tant que
Afficher J.
600*e0,6*J < 27000 ;
e0,6*J < 27 000 / 600 ; e0,6*J < 45 ; 0,6 J < ln(45) ; J < ln(45) / 0,6 soit environ 6 jours.
b. Interpréter cette valeur.
La limite de consommation est de l'ordre de 6 jours.
|
...
|
....
|
Exercice 2. (10
points).
Partie A.
40 % des spas sont équipés de lampe UV et parmi eux, 2 % présentent un problème de filtration.
Parmi les spas non équipés de lampe UV, 15% présentent un problème de filtration.
On choisit un spa au hasard et on note les événements :
L " spa équipé de lampe Uv".
F : " problème de filtration".
1. Compléter l'arbre pondéré suivant.
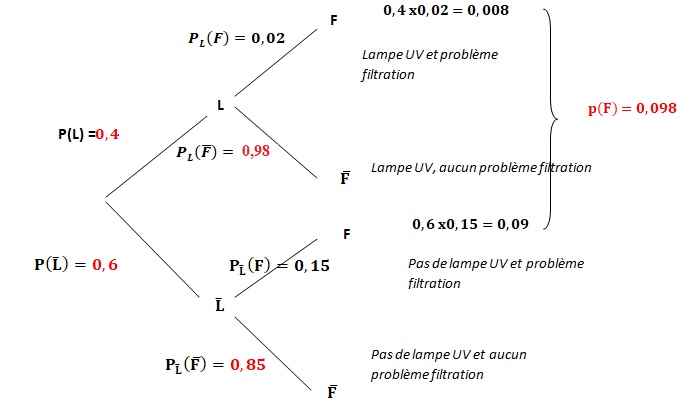
2. Montrer que p(F) = 0,098.
Formule des probabilités totales : 0,008+0,09 = 0,098.
3. Le spa choisit au hasard présente un problème de filtation. Calculer la probabilité qu'il ne possède pas de lampe UV.
PF( non L) =P(F n non L) / P(L) =0,09 / 0,098 ~0,918.
4. Lors d'une opération de maintenance sur 78 spas installés, le technicien compte 12 spas avec un problème de filtration.
a. Donner une estimation ponctuelle f de la proportion p des qpas présentant un problème de filtration.
f = 12 /78 ~0,154.
b. Déterminer par un intervalle de confiance au seuil de 95 % de cette proportion p.
1,96 ( p(1-p) / 100)½ =1,96 x(0,154 x0,846 / 78)½=0,080.
Intervalle de confiance : [0,154-0,080 ; 0,154 +0,080) soit [ 0,074 ; 0,234 ].
Partie B.
On
constate que la probabilité que la lampe UV d'un spa tombe en panne au
cours des trois premiers mois d'utilisation est p = 0,03.
On prélève au hasard un lot de 200 lampes dans la production. On
appelle X la variable aléatoire qui, à un lot de 200 lampes, associe le
nombre de lampes qui tomberont en panne au cours des trois premiers
mois d'utilisation.
1. Justifier que X suit une loi binomiale dont on précisera les paramètres.
On choisit 200 lampes de manière indépendante. Deux issues sont
possibles " la lampe tombera en panne " ou" la lampe ne tombera pas en panne".
On répète 200 fois une épreuve de Bernoulli.
X suit une loi binomiale de paramètre n =200 ; p = 0,03.
2. Calculer la probabilité P(X < 10) et interpréter.
P (X < 10)=0,960.
La probabilité qu'au plus 10 lampes UV tombent en panne au cours des trois premiers mois est égale à 0,960.
3.
Calculer
l'esprance de X et interpréter.
E = n p = 200 x 0,03 = 6.
En moyenne, 6 lampes tombent en panne au cours des trois premiers mois d'utilisation.
Partie C.
Cette loi peut être approchée par un loi de Poisson de paramètre l.
1. Justifier que l = 6.
l = np = 200 x0,03 = 6.
On note Y une variable aléatoire qui suit la loi de Poisson de paramètre l = 6.
2. Calculer P(Y=1).
P(Y=1)= 0,0149.
3. On admet que pour tout entier naturel k > 1 la probabilité de l'événement "Y = k" est donnée par :
P(Y=k) = lk e-l / (1 x 2 x...x k)
La proposition "P(Y=200)=0" est-elle vraie ou fausse ? Justifier.
P(Y=200) = 6200 xe-6 /200! ~0. Vrai.
|
|