Oscillateur harmonique, oscillateur anharmonique : stabilité, instabillité, Agrégation 2019. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. .. .. . . .. .. ...... ... Oscillateur harmonique. On considère un pendule élastique constitué d'un point matériel M de masse m astreint à se déplacer sur un axe horizontal Ox, fixe dans le référentiel d'étude supposé galiléen. L'origine des abscisses O constitue une extrémité d'un ressort de  raideur k de longueur à vide l0 dont l'autre extrémité est fixée au point M. Initialement le point M est lâché sans vitesse initiale depuis un point d'abscisse x0 > l0. Les frottements sont négligés. 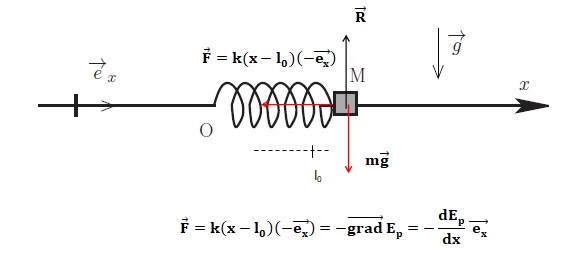1. Montrer que l'équation du mouvement de M peut se mettre sous la forme : x"+w02x=w02l0. M est soumis à son poids, verticale vers le bas, à l'action du support, opposé au poids et à la force de rappel exercée par le ressort  dirigée suivant l'axe Ox ( sens contraire de l'axe si le ressort est étiré) de valeur F = k(x-l0) avec x longueur du ressort. Ecrire la relation fondamentale de la dynamique, projetée sur l'axe Ox : mx" = -k(x-l0) mx" +kx = kl0 ; x"+k / m x = k / m l0. On pose w02= k / m. x"+w02x=w02l0. 2. Quelle(s) est (sont) la (les) force(s) qui travaille(nt) au cours du mouvement de M. Montrer qu'elle(s) dérive(nt) d'une énergie potentielle Ep(x) qu'on exprimera en rappelant au préalable les propriétés générales d'une fonction énergie potentielle. Le poids et l'action du support, perpendiculaires au support, ne travaillent pas. Seule la force de rappel exercée par le ressort travaille. L'énergie potentielle est une fonction de la position de M, x-l0 dans ce cas. Ep(x) = ½k(x-l0)2 + Cste. 3. Tracer l'allure de cette fonction Ep(x) et en déduire le domaine des valeurs de x accessibles au cours du mouvement. 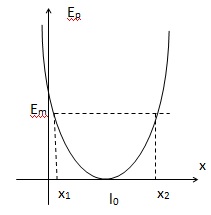Energie mécanique initiale : Em =Ep = ½k(x0-l0)2. Energie mécanique à la date t :  ½k(x-l0)2+½mv2. La seule force qui travaille étant conservative, l'énergie mécanique se conserve. ½k(x-l0)2+½mv2=½k(x0-l0)2. mv2=k(x0-l0)2 -k (x-l0)2 > 0. k( x0-x)(x+x0-2l0) >0. x2 = x0, position initiale ; x+x0-2l0=0 ; x1=2l0-x0. 4. Résoudre l'équation obtenue à la question 1. x"+w02x=0 ; solution : x = A cos (w0t) ; Solution particulière : x =l0 ; solution générale : x = A cos (w0t) + l0. A t = 0 : x = x0 et x' = -Aw0 sin((w0t) =0. x0 = A +l0 ; A = x0-l0. x = ( x0-l0 ) cos (w0t) +l0. 5. On généralise l'étude précédente dans le cas où M, toujours astreint à se déplacer sur l'axe horizontal Ox est soumis à une résultante des forces qui dérive d'une énergie potentielle E(x). On suppose qu'une position d'équilibre xe existe pour M. Quelle propriété possède l'énergie potentielle en x = xe ? En étudiant les petits mouvements de M autour de sa position d'équilibre, obtenir une condition sur d2E/dx2(xe) pour que cet équilibre soit stable  Que peut-on dire alors de E(x) en xe ? L'équation du mouvement s'écrit : m x" = -dE(x) / dx. A l'équilibre -dE(xe) / dx = 0. L'énergie potentielle E(x) atteint un extrémum en xe. On effectue un développement limité à l'ordre 1 de dE(x) /dx au voisinage de xe : dE(x) /dx = (x-xe) d2E(xe) /dx2 + e (x-xe). Au voisinage de la position d'équilibre : m x"= - (x-xe) d2E(xe) /dx2 ; mx" +x d2E(xe) /dx2 = xe d2E(xe) /dx2. Si d2E(xe) /dx2 >0 , on retrouve le cas de l'oxcillateur harmonique. ( équilibre stable). Dans le cas contraire, les solutions divergent et l'équilibre est instable. 6. Dans le cas du pendule élastique précédent, où se trouve sa position d'équilibre ? Est-il stable ou instable ? Ep(x) est minimale en x = l0. La position d'équilibre est stable. ... .... Oscillateur anharmonique : stabilité, instabilité, métastabilité. On considère la nouvelle configuration du pendule représentée ci-dessous. le point M est toujours astreint à se déplacer sur l'axe horizontal x'Ax en ne subissant aucun frottement. L'origine de x est prise en A. L'étude se fera dans le référentyiel galiléen où l'axe Ax est fixe. 7. Montrer que la résultante des forces s'appliquant sur M dans le référentiel d'étude dérive d'une énergie potentielle E'p(x). 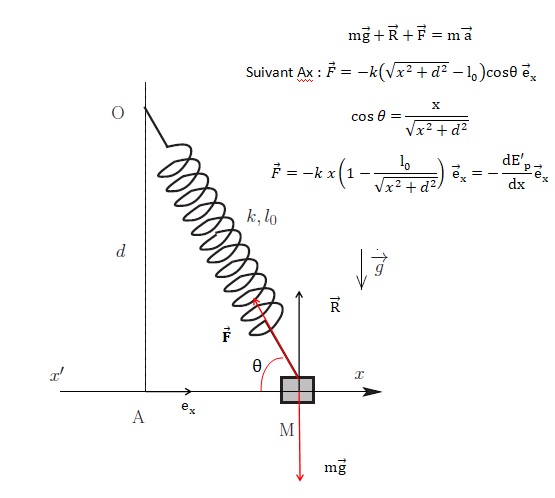E'p(x) =½k[ x2-2l0(d2+x2)½)] à une constante près. E'p(x) =½k((d2+x2)½ -l0)2+ Cste. On pose a = d / l0 : E'p(x) =½kl02[(a2+(x / l0)2)½ -1]2+ Cste. 8. Préciser les conditions d'équilibre dans les cas a <1 et a >1. On recherche pour quelles valeurs de x la fonction E'p(x) est etrémale. dE'p(x) / dx = 0. dE'p(x) / dx =kx[1-(a2+(x / l0)2)-½ ] =0. Les racines sont : x =0 ; x = ±l0(1-a2)½. Pour a >1, il y a une seule position d'équilibre x = 0. Pour a <1, il y a trois positions d'équilibre x = 0 et x = ±l0(1-a2)½. 9. Tracer dans chacun des cas, l'allure de la fonction E'p(x). Qu'en déduire quant à la stabilité des différentes positions d'équilibre ? 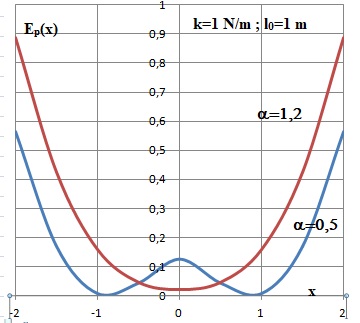Pour a >1, la position d'équilibre x = 0 et stable. Pour a < 1, la position d'équilibre x = 0 et instable et les deux autres positions d'équilibre x = ±l0(1-a2)½ sont stables. 10. On considère le cas a >1. Déterminer l'équation des petits mouvements autour de la ( les) position(s) d'équilibre stable(s). Montrer que ce mouvement se ramène à celui d'un oscillateur harmonique dont on exprimera la période Tsup en fonction de k, m et a. Relation fondamentale de la dynamique en projection sur l'axe horizontal : mx"= -kx [1-(a2+(x / l0)2)-½ ]. x"+k / m x [1-(a2+(x / l0)2)-½ ]=0. x"+w02 x [1-(a2+(x / l0)2)-½ ]=0. xe=0 ; pour les petits mouvements autour de cette position d'équilibre, on effectue un développement limité de (a2+(x / l0)2)-½ : (a2+(x / l0)2)-½ =1 /a(1+(x / (al0))2)-½ =1/ a(1-(x / (2al0))2). Repport dans l'équation différentielle du mouvement en ne conservant que les termes d'ordre 1 en x : x"+w02 x (1-1/ a )=0. Il s'agit de l'équation d'un oscillateur harmonique de pulsation w0 (1-1/ a )½. Tsup = 2p / w0 (1-1/ a )-½= T0[ a /(a-1)]½. 11. On considère le cas a <1. Déterminer l'équation des petits mouvements autour de la ( les) position(s) d'équilibre stable(s). Montrer que ce mouvement se ramène à celui d'un oscillateur harmonique dont on exprimera la période Tinf en fonction de k, m et a. Même méthode avec xe = ±l0(1-a2)½ = dl0(1-a2)½ . Les petits mouvement autour de la positions d'équilibre conduisent à x= xe + u avec u << | xeq| < l0. L'équation du mouvement s'écrit : Le terme u2 / l02 est négligeable devant u / l0 et d2=1 : u"+w02 (1-a2)u=0. Il s'agit de l'équation d'un oscillateur harmonique de pulsation w0 (1- a2 )½. Tinf = 2p / w0 (1- a2 )-½= T0[ 1- a2 ]-½. 12. Interpréter brièvement la valeur obtenue pour Tinf quand a = 0. Proposer une explication physique pour les valeurs obtenues pour Tsup et Tinf quand a --> 1. Pour de petites valeurs de a ( d tend vers zéro, A et O sont confondus), Tinf tend vers T0. Quand a tend vers 1, Tsup et Tinf tendent vers l'infini. Le mobile écarté de sa position d'équilibre met un temps très long pour y revenir, le potentiel variant peu autour de cette position.

menu