Physique
chimie, expériences historiques sur la chute des corps.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
..
..
|
.
.
|
..
..
......
...
|
Dans
toute cette première partie, le référentiel terrestre est supposé
galiléen. On note t la variable associée au temps et g l’intensité du
champ de pesanteur terrestre (on prend g≈10 m.s−2 et on considère ce champ uniforme). On néglige également l’effet de la poussée d’Archimède.
Pour Aristote, la vitesse de chute d’un mobile est proportionnelle à son poids.
Cependant, Galilée proposa l’expérience de pensée suivante : […].
Considérons deux masses m1 et m2< m1 en chute libre. D’après Aristote, la masse m1 atteint le sol avant la masse m2. En reliant, à l’aide d’un fil, les masses m1 et m2, on obtient alors un système (S) plus lourd que la masse m1 seule et donc a priori plus rapide pendant sa chute. Cependant ce système (S) est ralenti par la masse m2 (m2 plus lente faisant l’effet « d’un parachute »). (S) est donc plus lent que la masse m1
seule alors qu’il est plus lourd, il y a donc un paradoxe…. Étienne
Klein, extrait d’une conférence intitulée « De quoi l’énergie est-elle
le nom ? »
En 1602, Galilée a l’intuition que le mouvement de chute libre
(c’est-à-dire sans frottement) d’un corps dans le champ de pesanteur
terrestre est indépendant de la masse de ce corps. Mais il se heurte à
l’impossibilité de mesurer précisément la vitesse d’un corps tombant à
la verticale. Galilée entreprit alors d’étudier le mouvement de chute
de corps à l’aide d’un plan incliné d’un angle a
par rapport à l’horizontale. On note Oz l’axe vertical ascendant et Ax
l’axe confondu avec la ligne de plus grande pente du plan incliné. On
pose OA =h.
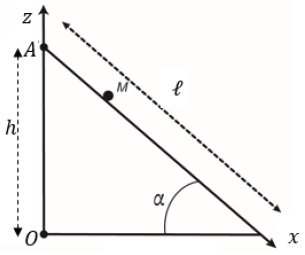
Ne disposant pas de chronomètres précis, Galilée fait rouler des billes
sur un plan incliné en faisant teinter des chlochettes que la bille
fera sonner en passant.. Il dispose ces chlochettes à intervalles
variables sur le plan jusqu'à obtenir un son régulier.
Le tintement est régulier lorsque les chlochettes sont placées à des intervalles 1, 3, 5, 7...
En une unité de temps, la bille parcourt une unité de distance.
En 2 unités de temps, la bille parcourt 3+1=4 unités de distance.
En 3 unités de temps, la bille parcourt 5+3+1=9 unités de distance.
On
souhaite étudier cette expérience de Galilée en analysant le mouvement
d’un mobile, assimilé à un point matériel de masse m repéré par le
point M, lâché sans vitesse initiale depuis le point A. On néglige tout
frottement lors de cette chute s’effectuant sur le plan incliné .
Q1. Déterminer, à l’aide de la relation fondamentale de la dynamique, l’accélération x" ̈(t)= a du point M en fonction de g et a.
Le système est soumis à son poids et à l'action du plan.
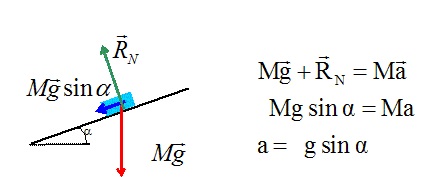
. Q2. Exprimer le temps de chute t0 nécessaire pour parcourir, suivant la ligne de plus grande pente, la distance ℓ en fonction de g, h et ℓ. Commenter.
La vitesse est une primitive de l'accélération et la vitesse initiale est nulle : v(t) = g sin a t avec sin a = h / l.
La position est une primitive de la vitesse et la position initiale est l'origine de l'axe Ax.
x =½g h / l t2.
l =½g h / l t02; t02=2l2 / (gh) ; t0 = l (2 /(gh))½.
Si le temps double, alors la hauteur h quadruple ; si le temps double,
la distance parcourue sur le plan incliné est multipliée par 4.
Pour un mobile partant du repos et en négligeant les frottements, la distance parcourue est proportionnelle au carré du temps.
Q3. Un enseignant pose la question à choix multiple suivante :
Soient deux points matériels P1 et P2 de masses respectives m1 et m2 (m2 < m1).
On lâche ces deux masses, sans vitesse initiale, d’une hauteur h sur un
plan incliné. Quel mobile touche le sol en premier ? On néglige l’effet
des frottements. »
A) P1 ; B) P2 ; C) P1 et P2 touchent le sol en même temps.
15 élèves répondent A) et 20 répondent C).
Proposer une remédiation.
Expérience du tube de Newton dans lequel on fait le vide. Une feuille
et une bille en acier partant du repos, touchent en même temps le sol.
|
...
|
....
|
b) Saut en chute libre de Felix Baumgartner.
Le 14 Octobre 2012, s’élevant en ballon à 39 kilomètres d’altitude pour
effectuer un saut en chute libre, l’Autrichien Felix Baumgartner
quittait la troposphère, la première couche de l’atmosphère terrestre.
[…]. Il est incontestable que F. Baumgartner a franchi le mur du son.
Cependant, […] il est peu probable que cela ait créé une onde de choc
notable […]. Il est par ailleurs mentionné que ce saut pourra alimenter
la réflexion sur les procédés de survie des astronautes lors d’un
retour sur Terre : au lieu d’attendre la destruction de leur vaisseau
spatial dans les hautes couches de l’atmosphère, ne peuvent-ils pas sauter sur Terre et revenir comme F. Baumgartner ?
Le graphe 1 ci-dessous donne l'évolution de la vitesse en chute réelle en fonction du temps.
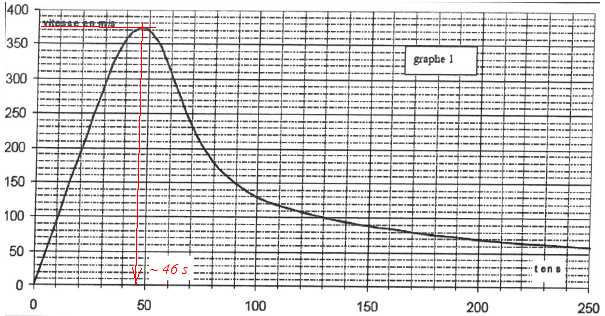
Le graphe 2 donne l'évolution de
l'altitude de F.Baumgartner en fonction du temps, enregistrée à l'aide
de 4 balises GPS placées dans sa combinaison.
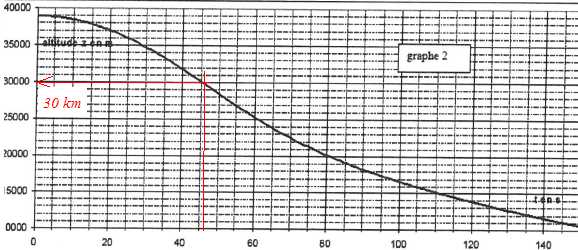
Q4. Estimer en explicitant la méthode, l’épaisseur d de l’atmosphère dans laquelle F. Baumgartner est en chute libre (mouvement de chute
pour lequel on néglige les frottements).
D'après
le graphe 1, la courbe est un segment de droite entre t=0 et t=40 s. La
chute est donc libre. Par contre entre 40 et 46 s, la courbe n'est pas
une droite et la chute n'est plus libre.
Altitude de départ : 39 km ; altitude atteinte à t = 40 s : 32 km ; d = 39-32 = 7 km.
L’étude du mouvement de chute pendant les 250 premières secondes
nécessite de prendre en compte les frottements de l’air : dans ces
conditions la vitesse de chute d’un mobile est fonction de la masse de
ce mobile. En effet, lorsque F. Baumgartner atteint sa vitesse limite
pour t=200 s, il se trouve à 10 km d’altitude et à une pression
atteignant déjà 20 % de la pression au niveau du sol égale à 1,0 x 105 Pa. Pour t ≤ 250 s, on supposera l’atmosphère isotherme et à la température 𝛳0=−50 °𝐶 (on donne également la valeur de la masse molaire 𝑀 de l’air : 𝑀=29 g.mol−1 et on rappelle la valeur de la constante des gaz parfaits R=8,3 J.K−1.mol−1).
Pendant cette étude, le champ de pesanteur pourra toujours être
considéré uniforme et égal à g. F. Baumgartner, de masse m, est animé
d’une vitesse 𝑣⃗(𝑡)=𝑣(𝑡𝑡) 𝑢𝑧⃗ par rapport au référentiel
terrestre (le vecteur 𝑢𝑧⃗ est associé à un axe Oz vertical et
ascendant, l’origine O étant prise au niveau du sol). Si nécessaire, il
est possible de modéliser l’action de l’air sur F. Baumgartner par une
force de traînée dont la puissance est donnée par l’expression 𝑃𝑓(𝑡)=0,5𝜌(𝑧 )𝐴C𝑣3
où 𝜌(𝑧 ) est la masse volumique de l’atmosphère terrestre, 𝐴 est la
surface apparente de F. Baumgartner et 𝐶 est le coefficient de traînée
dans l’air (𝐴 et 𝐶 sont supposés constants).
Q5. Résolution de problème : estimer la valeur de la masse volumique de l’air ainsi que celle de la côte verticale 𝑧0 de F. Baumgartner lorsqu’il atteint sa vitesse maximale. Pourquoi l’onde de choc émise en 𝑧0 n’est pas « notable » ?
Lorsque la vitesse maximale est atteinte, le poids de F Baumgartner compense les forces de frottement dues à l'air.
Masse de F. Baumgartner et de son équipement : m = 120 kg.
Vitesse maximale atteinte : 1342 km / h soit 1342 / 3,6 ~373 m /s.
Surface de référence A = 0,4 m2 ; coefficient de traînée C = 1,1 .
mg = 0,5 AC r v2 ; r =2 x120 x10 /(0,22 x3732)~0,08 kg m-3.
Pression à cette altitude, l'air étant assimilé à un gaz parfait :
p V= nRT ; p = m / (M(air) V) RT = r /M(air) RT =0,08 / 0,029 *8,3 *(273-50)=5,1 103 Pa.
On suppose que pour des altitudes
comprises entre 11 km et 20 km, la température T de
l'atmosphère est constante.
On supposera que g garde une valeur
constante.
On donne la pression à l'altitude z :
p(z) =p0
exp(-M(air)g z / (RT)).
ln(p(z) / p0) = -M(air)g z /(RT).
z = -RT ln(p(z) / p0) / (M(air) g) =-8,3 *(273-50) ln(5,1 103 / 1,0 105) / (0,029 *10)~19 km.Expériences historiques sur la chute libre.Expériences historiques sur la chute libre.
|
|