Mathématiques. Concours CAPLP 2020. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. .. .. . . .. .. ...... ... Exercice 1. 2020. Préciser si chacune des propositions suivantes est vraie ou fausse, puis justifier la réponse. 1. La matrice suivante est-elle inversible ? Non. Le déterminant de la matrice étant nul, elle n'est pas inversible.  2. La relation suivante est-elle égale à 2 ? Vrai. Somme des termes d'une suite géométrique de raison 1 /2. 3. Soit f la fonction définie sur [-1 ; 1] par  : La fonction f est continue sur [-1 ; 1] et dérivable sur ]-1 ; 1[. vrai. La fonction est impaire ; le graphe est symétrique par rapport à l'origine. Au voisinage de zéro : 4. On considère un cône C dont le diamètre de la base et la hauteur mesurent 1 unité, et une boule B de diamètre 1 unité. Les volumes de C et de B sont dans le ratio 1 / 2. vrai. Volume du cône : pR2 H / 3 =3,14x0.52/3 ; volume de la boule : 4 /3 pR3=4 x3,14 x0,53/3 Les volumes de C et de B sont dans le ratio 1 / 2.   5. On a la relation : Faux. On pose u = -(1+x2)-½ ; u' = x / (1+x2)-3/2 ; 6. Soit la suite (un) définie par un = cos(n) sur N*et la suite (vn) définie par vn = 1 / n½ sur N* La suite (unvn) converge  et sa limite en plus l'infini est zéro. Vrai. cos(n) est compris entre -1 et +1 ; 1 / n½ tend vers zéro si n tend vers l'infini ; la limite de la suite (unvn) en plus l'infini est zéro. ... ....   7. La documentation technique d'une machine fabriquant des pièces dans une usine indique que, quand la machine est bien réglée, les pièces présenteront un défaut dans 0,8 % des cas. On s'intéresse à un échantillon de 800 pièces prélevées au hasard dans le stock. On suppose que le stock est suffisamment grand pour que l'on puisse assimiler cela à un tirage au sort avec remise. Un intervalle de fluctuation asymptotique de la fréquence des pièces sans défaut au seuil de 95 % est [0,985 ; 0,999]. Vrai. p = 0,008 ; 1-p =0,992 ; n = 800 ; 1,96 [p(1-p) /n]½ =0,0062. Intervalle de fluctuation asymptotique : [0,992 -0,0062 ; 0,992 +0,0062) soit [0,985 ; 0,999]. 8. Soit la fonction f définie sur R-{-1 ; 1} par f(x) = (x3+2x2) / (x2-1). La courbe représentative admet une asymptote oblique en -oo et en +oo. Vrai. (x3+2x2) / (x2-1) =x+2+(x+2) / (x2-1). f(x) -(x+2) =(x+2) / (x2-1). f(x) -(x+2) tend vers zéro en plus l'infini et en moins l'infini. La droite d'équation y = x+2 est asymptote à la courbe représentative. 9. L'équation différentielle y" -3y' +2y = x2-3x a pour ensemble de solutions réeeles : A ex+ B e2x. Faux. Equation sans second membre :y" -3y' +2y =0. Equation caractéristique : r2-3r+2 = 0; solutions r = 1 et r = 2. Solution générale de y" -3y' +2y =0  : y =A ex+ B e2x. Il faut ajouter une solution particulière, par exemple ½x2-½. y = A ex+ B e2x+½x2-½. 10. Dans le plan euclidien rapporté à un repère orthonormé Oxy, soit D la droite d'équation x+y+1 =0 et soit G le cercle d'équation x2+y2-2x-1=0. La droite est tangente au cercle. Vrai. y = -x-1; x2 +(-x-1)2-2x-1=0 ; x2 +x2+2x+1-2x-1=0 ; 2x2 = 0 soit x=0 et y =-1. Le cercle et la droite possèdent un seul point d'intersection.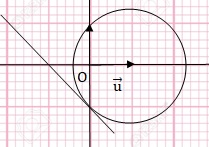 11. On considère une variable aléatoire X qui suit la loi exponentielle de paramètre l. On sait que P(X < 20) = 0,5. l = 1 /20. Faux. P(X < 20) =1-e-20 l = 0,5 ; e-20 l = 0,5 ; -20 l =ln (0,5) ; l = ln(2) /20.  12. On considère la fonction g dans C qui à tout nombre complexe z associe le nombre complexe g(z) =z2 +2z+9. dans le plan complexe, l'ensemble des points M d'affixe z tels que g(z) soit un nombre réel est une droite. Faux. z = x+iy ; g(z) = (x+iy)2 +2(x+iy) +9. g(z) = x2-y2+2i xy +2x+2i y+9 ; la partie imaginaire est nulle soit 2xy+2y =2y(x+1)=0. y=0 ou x = -1. L'ensemble des points cherchés appartiennent à la droite d'équation y = 0 et à la droite d'équation x = -1.

menu