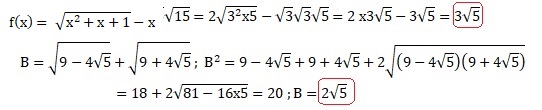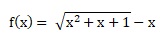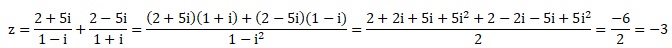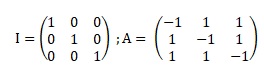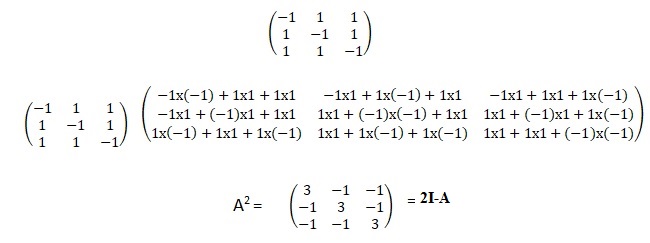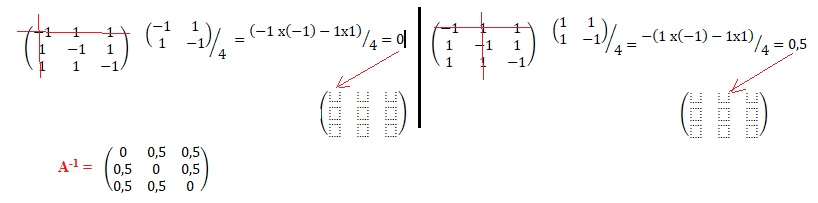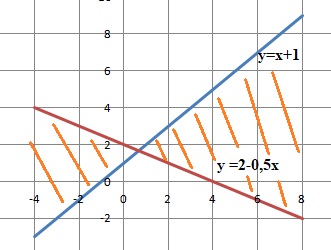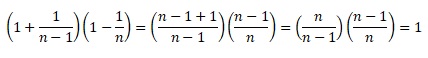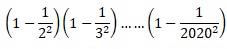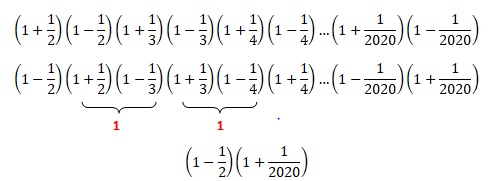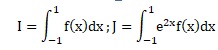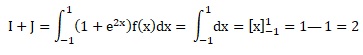Mathémmatiques,
concours EMIA 2020. Ecole militaire interarmes.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
..
..
..
.....
|
Exercice 1.
1. Ecrire sous la forme a x racine carrée (5) où a est un réel.
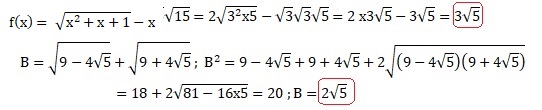
2. Montrer que la fonction suivante est définie sur R et calculer ses limites en plus l'infini et moins l'infini.
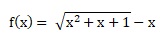
x2+x+1 = (x+1)2-x.
x+1 > x ; (x+1)2 > x.
Le terme sous le radical est défini quel que soit x réel.
f(x) est définie sur R.
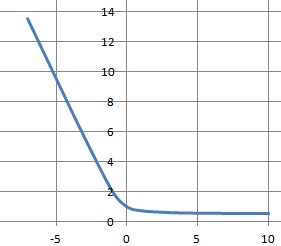
Quand x tend vers plus l'infini :
f(x) tend vers 0,5.
Quand x tend vers moins l'infini :
le terme sous le radical tend vers plus l'infini ; -x tend vers plus l'infini.
f(x) tend vers plus l'infini.
3. Soit le nombre complexe z1 = i +racine carrée(3) = i +3½.
Donner la forme exponentielle de z1.
|z1| =(1+3)½ = 2.
z1 = 2(3½ /2 +i /2)=2 (cos (p/6) + i sin (p/6) = 2 exp(ip/6).
4. Déterminer la partie réelle et la partie imaginaire du nombre :
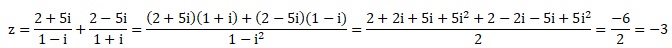
5. Résoudre dans R l'équation : ex-e2x-5=0.
On pose X = ex >0.
X-X2-5=0 ; X2 -X+5=0 ; D = (-1)2-4*5 = -19.
Le discriminant étant négatif, il n'y a pas de solution réelle.
6. Calculer les fonctions dérivées des fonctions suivantes :
f(x) = ln(x) / (1+x2).
On pose u = ln(x) et v = 1+x2 ; u' = 1 /x ; v' = 2x.
(u'v-v'u) / v2 =[(1+x2) / x - 2xln(x)] / (1+x2)2.
g(x) = x exp(x2+x+1).
On pose u = x et v = exp(x2+x+1).
u' = 1 ; v'= (2x+1) exp(x2+x+1).
u'v +v'u =exp(x2+x+1) +x(2x+1)exp(x2+x+1) = (2x2+x+1) exp(x2+x+1).
7. Déterminer une primitive pour chacune des fonctions suivantes.
f(x) = x7 +x5 +x3 +x.
F(x) = x8 /8 + x6 / 6 +x4 /4+x2 / 2.
g(x) = x exp(x2).
On pose u = x2 ; u' = 2x.
g =0,5 u' eu ; Primitive G= 0,5 exp(x2).
h(x) = 1 /(x ln(x)).
On pose u = ln(x) ; u' = 1 /x.
h = u' / u ; primitive : H = ln(ln(x)).
8. Montrer que l'équation sin(x) = 0,25 admet une unique solution a sur l'intervalle [0 ; p / 2 ] et donner la valeur exacte de cos(x).
sin(x) = sin(a) ;
x = a ~14,5° ; x = p-a n'appartient pas à [0 ; p / 2 ].
sin2(x) + cos2(x) = 1 ; cos2(x) = 1-(1/4)2 =15 / 16.
cos(x) = ± racine carrée (15 / 16).
|
.
.
|
Matrices.
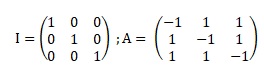
1. Calculer A2 en fonction de I et A.
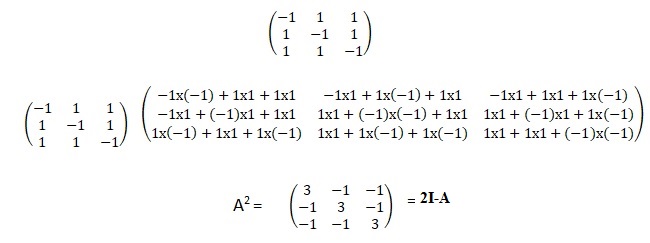
2. En déduire que A est inversible et calculer son inverse.
Calcul du déterminant associé à A :
D =(-1)(-1)(-1) +1 x1x1+1 x1 x 1-[1 x(-1)x1 +1 x(-1) x1+(-1) x1 x1] =4.
Le déterminant étant différent de zéro, A est inversible.
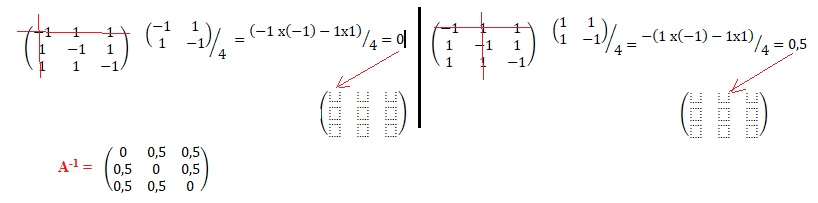
3. Démontrer que pour tout entier naturel n, la matrice An s'écrit sous la forme aI + bA avec a et b réels.
Initialisation : la propriété est vraie au rang 2.
Hérédité : la propriété est supposée vraie au rang p : Ap = a'I+b'A.
Ap+1 =ApxA= a'I x A+b'A2 =a'I x A+b'(2I-A) avec I A = A.
Ap+1 =a' A+2b' I-b' A = 2b' I +(a'-b') A = aI+bA.
Conclusion : la propriété est vraie au rang 2 et héréditaire. Elle est vraie pour tout n entier naturel.
Inéquations.
Représenter graphiquement l'ensemble des solutions de l'inéquation : (x+1-y)(2y+x-4) > 0.
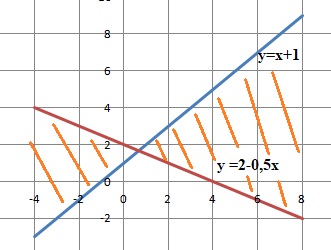
Zone hachurée y compris les droites.
|
..
..
|
. .
|
Géométrie.
On définit trois plans par les équations cartésiennes suivantes :
P1 : x+y-z=0.
P2 : x-y-2=0
P3 : y-z-3=0.
1. Déterminer les coordonnées d'un vecteur normal à P1 de norme 1.
Coordonnées ( k ; k ; -k) avec k réel
Norme 1 = (k2 +k2 +(-k)2)½ =3½k ; k =1 / 3½.
2. Existe-t-il une droite incluse dans P2 parallèle à l'axe Oz ?
Coordonnées d'un vecteur directeur d'une droite parallèle à l'axe Oz : (0 ; 0 ; 1).
Equation paramétrique de cette droite : x = a ; y = ß ; z =t+g avec t réel.
Si la droite est incluse dans le plan P2 : a-ß-2 = 0.
3. Déterminer l'intersection des trois plans.
Intersection de P1 et P3 :x+y-z =y-z-3 ; x = -3.
Intersection de P1 et P2 : x+y-z =x-y-2 ; 2y-z+2=0.
Intersection de P2 et P3 : x-y-2 =y-z-3 ;
-3-y-2 =y-z-3 ; 2y-z+2=0.
Jeu.
Un joueur s'initie à un jeu en effectuant plusieurs parties
successives. Pour la première partie, les probabilités de gagner et de
perdre sont égales. Pour les parties suivantes, on suppose que si une
partie est gagnée, alors la probabilité de gagner la suivante est 0,6.
Si la partie est perdue, la probabilité de perdre la suivante est 0,7.
On note Gn l'événement " gagner la partie n".
On note un = P(Gn) et vn= P( non Gn).
1. Justifier que un+1 = 0,6 un +0,3 vn.
u1= 0,5 ; v1 = 0,5.
u2 = 0,6 u1 +0,3 v1.
u3 =0,6 u2 +0,3 v2.
un+1=0,6 un +0,3 vn.
2. De même, exprimer vn+1 en fonction de un et vn.
v2 = 0,4 u1 +0,7 v1.
v3 =0,4 u2 +0,7 v2.
vn+1=0,4 un +0,7 vn.
3. En déduire une fonction f telle que la suite (un) soit définie par un+1 = f(un).
La probabilité de gain ajoutée à celle de perdre est égale à 1.
un+1 +vn+1 = un +vn =1.
vn+1 = 1 -un+1 ; vn = 1 -un.
un+1=0,6 un +0,3(1- un) = 0,3 un +0,3.
f(un) = 0,3( un+1).
4. Vérifier que l'équation f(x) = x admet une seule solution réelle, notée a.
0,3x +0,3 = x ; 0,3 = 0,7 x ; a = 3 /7.
5. Démontrer que la suite (wn) de terme général un-a est géométrique.
wn =un-a.
wn+1 =0,3 (un +1)-3 / 7 = 0,3un +3 /10 -3 /7 =0,3un +(21-30) /70 =3 /10 un -9 / 70=3 /10 (un -3 /7)=0,3 wn.
wn+1 / wn = 0,3.
6. En déduire une expression de un en fonction de n.
wn =w1 x 0,3n = (u1-3 / 7)0,3n =(1 / 2 -3 / 7) 0,3n =1 / 14 x 0,3n =un-3 /7.
un=3 /7 + 1 /14 x 0,3n.
7. Que devient la probabilité de gain après un grand nombre de parties ?
Quand n devient grand, 0,3n tend vers zéro.
Probabilité de gain après un grand nombre de parties : 3 /7 ~0,43.
|
Probabilités.
Une entreprise fabrique des ampoules dont 80 % ont une durée de vie
strictement supérieure à 3000 heures. Un échantillon de taille n est
assimilé à un tirage avec remise de n ampoules parmi la
production. Soit X la variable aléatoire donnant le nombre d'ampoules
ayant une durée de vie inférieure ou égale à 3000 heures dans un
échantillon de taille 15.
1. Déterminer la loi de la variable X.
Loi binomiale. Les ampoules durent plus de 3000 heures ( p = 0,8) ou
bien ont une durée de vie inférieure ou égale à 3000 heures ( q = 1 -p
= 0,2).
2. Quelle est la
probabilité que dans cet échantillon, toutes les ampoules aient une
durée de vie strictement supérieure à 3000 heures ?
P( X =15) = 0,035.
3.
Quelle est la probabilité que dans cet échantillon, on trouve plus de 2
ampoules qui aient une durée de vie strictement supérieure à 3000
heures ?
P(X > 2) =1-P(X <2) =1-5,7 10-8 ~1.
Un calcul.
1. Pour n > 2, simplifier le produit :
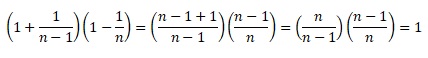
2. En déduire un calcul numérique simple du produit :
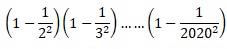
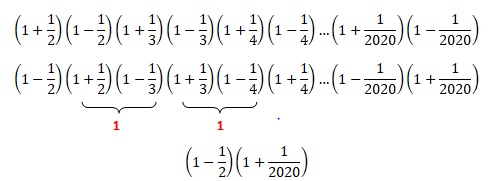
Etude de fonction.
Soit la fonction f définie sur R par : f(x) = 1 /(e2x+1). On note C sa courbe représentative.
1. Déterminer les limite de f en plus l'infini et en moins l'infini.
En plus l'infini, e2x tend vers plus l'infini ; e2x+1 tend vers plus l'infini et f(x) tend vers zéro.
En moins l'infini, e2x tend vers zéro ; e2x+1 tend vers 1 et f(x) tend vers 1.
2. Calculer la dérivée f '(x).
On pose u = e2x+1 ; u' =2e2x.
f = u-1 ; f ' = -u' u-2 ; f ' (x) = -2e2x / (e2x+1)2.
e2x / (e2x+1)2 >0 ; f '(x) <0, f(x) est strictement décroissante.
3. Dresser le tableau de variations de f.
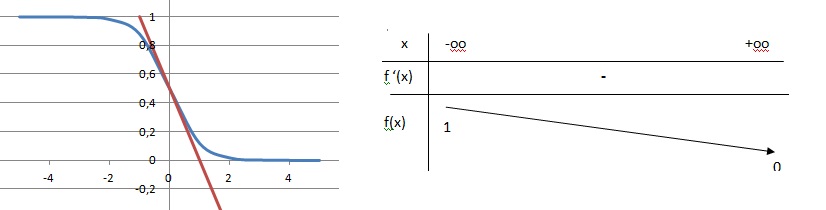
4. Déterminer une équation de la tangente à C au point d'abscisse zéro.
Coefficient directeur : f '(0) = -2 / 4 = -0,5.
La tangente passe au point de coordonnées ( 0 ; f (0) =0,5).
y = -0,5 x+0,5.
5. Soit les intégrales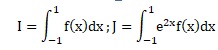
a. Justifier que (e2+1) / (e-2+1) = e2.
(e2+1) / (1 /e2+1) =(e2+1)e2 / (1 +e2) = e2.
b. Calculer la dérivée de H(x) =0,5 ln(e2x+1).
On pose u = e2x+1 ; u' = 2e2x ; H'(x) = 0,5 u' / u = e2x / (e2x+1).
c. En déduire le calcul de J.
H est une primitive de e2x f(x).
J = H(1)-H(-1) = 0,5 [ ln(e2+1)- ln(e-2+1)].
J = 0,5 ln [(e2+1) /(e-2+1)]= 0,5 ln(e2) =2 x0,5 ln(e) = 1.
d. Calculer I+J et en déduire une valeur de I.
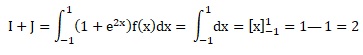
I+J = 2 et J = 1 ; I = 1.
Algorithme.
On considère l'algorithme suivant :
Entrée : T tableau de nombres entiers naturels.
n prend la valeur (longueur de T)
Pour k allant de 1 à n-1 faire
x prend la valeur T(k)
j prend la valeur k.
tant que j >0 et T(j-1) >x faire
T(j) prend la valeur T(j-1)
j prend la valeur j-1
Fin tant que
T(j) prend la valeur x
Fin pour
Sortie : T.
Appliquer l'algorithme au tableau T = [ 3, 8, 2] en donnant les valeurs
de x, j, T(0), T(1), T(2) à chaque étape et exprimer la sortie.
n=3.
Etape
|
k=1
|
k=2
|
x
|
T(1)=8
|
T(2)=2
|
j
|
1
|
2
|
| j >0 et T(j-1) >x |
Faux
|
Vrai
|
Boucle tant que
|
T(j)
|
T(1)=8
|
j
|
0
|
| j >0 et T(j-1) >x |
Faux
|
|
|
T(0) =3
|
Sortie : T(2), T(1), T(0).
..
|
|
|