Math�matiques,
datation d'une roche, �tude d'une huile moteur.
Concours interne TSPEI 2019.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicit�s adapt�es � vos centres
d’int�r�ts.
..
..
|
|
......
.....
|
Exercice 1.
Soit un circuit comprenant un g�n�rateur de fem E, une bobine de
r�sistance R et d'inductance L et un interrupteur. A la date t apr�s la
fermeture de l'interrupteur, l'intensit� du courant est i(t) = I (
1-exp(-t / k)).
I = E / R et k = L / R, constante de temps.
On se propose d'�tudier la fonction i(t) sur [0 ; +oo[. On note C sa
courbe repr�sentative.
1.
Calculer i(0).
i(0) = I (1-1) = 0.
2. D�terminer la limite de i(t)
quand i tend vers +oo. Que peut-on en d�duire pour la courbe C ?
Le terme en exponentielle tend vers z�ro et i(t) tend vers I = E / R (
r�gime permanent).
La courbe C admet une asymptote horizontale d'�quation i(t) = I= E / R.
3. Calculer la d�riv�e de la
fonction i et en d�duire le tableau de variation de i.
i'(t) = I / k e-t / k = E / L e-t / k .
La d�riv�e �tant positive, la fonction i(t) cro�t de 0 � I = E / R.
4. D�terminer une
�quation cart�sienne de la tangente T � la courbe au point d'abscisse t
= 0.
Coefficient directeur de cette tangente : i'(0) =E / L.
Equation de la tangente i(t) = E / L t.
5. Construire la
cournbe C et la tangente T en prenant I = 1 et k = 0,5.
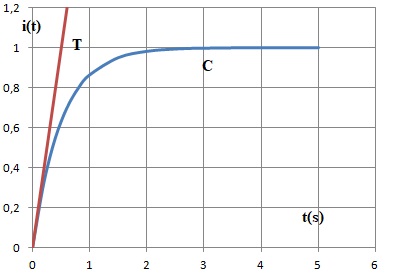
6. A partir de quel
temps ( exprim� � l'aide de k ) peut-on affirmer que i(t) sera
sup�rieur � 0,99 I ?
1-exp(-t
/ k) > 0,99 ; exp(-t
/ k) < 0,01 ;-t / k < ln(0,01) ;
t > k ln(100) ; t > 4,6 k.
Exercice 2.
Soient les nombres complexes z1 = -1 +i 3� et z2
= -1-i 3�.
1. D�terminer les
modules de ces nombres ainsi que leurs arguments..
Ces nombres complexes �tant conjugu�s, ils ont le m�me module :
|z1| =|z2| =( (-1)2 +(3�)2)�
=(1+3)� = 2.
z1 / |z1| = -0,5 +i 3� / 2 =cos(2p/3) + i sin(2p/3)
z1 = 2 (cos(2p/3) + i sin(2p/3)) = 2 exp(i2p/3).
z2 = 2 (cos(-2p/3) + i sin(-2p/3)) = 2 exp(-i2p/3).
2. Calculer z13
puis z23.
z13
=23 exp(i2p)
= 8.
z23 =23 exp(-i2p)
= 8.
3. En d�duire les
solutions dans C de l'�quation (E) : z3 = 1.
Une solution r�elle zA = 1.
Deux racines complexes :(z-1) ( z2 +bz+c) = 0.
z3+bz2 +cz -z2 -bz -c =z3-1.
On identifie : c = 1 ; b = c = 1.
z2 +z+1 =0 ; discriminant D = 12-4 = -3 = 3
i2.
Solutions zB = (-1 +i 3�) / 2 = z1 / 2.
zC = (-1 -i 3�) / 2
= z2 / 2.
4. Dans le plan
complexe, construire les points dont les affixes respectives sont les
solutions de (E).
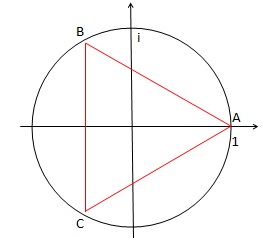
5. D�montrer que le
triangle obtenu est �quilat�ral dont on pr�cisera la longueur d'un c�t�.
AB =|zB-zA| = ( -1,52 +(3�
/ 2)2)� =3�.
AC =|zC-zA|
= ( -1,52 +(-3� / 2)2)� =3�.
BC =|zC-zB|
= ( 02 +( 3�)2)� =( 12)�
= 3�.
|
...
|
|
|
....
|
Datation
d'une roche. M�thode du potassium-argon.
Les
roches volcaniques contiennent du potassium et en particulier un
isotope radioactif, le potassium 40. Ce dernier se transforme en argon
qui se trouve pi�g� dans la roche. Au cours du temps la quantit� de
potassium 40 d�cro�t suivant 2 modes de transformations spontan�e :
89,5 % des noyaux subissent une d�sint�gration �-.
10,5 % subissent une capture �lectronique selon : 4019K
+0-1e--> 4018Ar.
Pour dater la roche on utilise la relation NAr(t) / NK(t)
= 0,105 (elt-1)
(1) avec l= 5,81
10-11 an-1.
1. Quelle est la
nature d'une particule �-. Ecrire l'�quation de la
d�sint�gration correspondant au premier mode de transformation.
Une particule �- est un �lectron not� 0-1e.
4019K
-->AZX + 0-1e.
Conservation du nombre de masse : A = 40.
Conservation de la charge : 19 = Z-1 ; Z = 20 ( �l�ment calcium Ca)
2. D�finir
demi-vie radioactive et calculer sa valeur pour la seconde
transformation.
La demi-vie not�e t� est la dur�e au bout de laquelle,
l'activit� initiale est divis�e par 2.
lt�=
ln (2) ; t� = ln(2) / (5,81 10-11) =1,19 1010
an.
1.3. On se propose
de retrouver la relation (1).
1.3.a . Rappeler la
loi de d�croissance radioactive.
NK(t) = NK(0) exp (-lt).
1.3.b. compte tenu
de l'hypoth�se de la seule capture �lectronique, quelle relation
peut-on �crire entre NAr(t) et NK(t) et NK(0).
NAr(t)
= 0,105 (NK(0)
- NK(t)).
1.3.c. En d�duire NAr(t)
= 0,105NK(t) ( exp(-lt)-1).
NAr(t)
= 0,105 (NK(t)
exp (lt)
- NK(t)) = 0,105 NK(t)
(exp (lt) -1).
1.4. Des ossements ont �t�
d�couverts entre deux couches de tuf volcanique. On date ces ossements
par la m�thode du potassium 40.
|
Argon
40 ( mol par g d'�chantillon)
|
Potassium
40 ( mol par g d'�chantillon) |
Tuf
1
|
2,260
10-11
|
1,667
10-7
|
Tuf
2
|
2,242
10-11
|
2,604
10-7 |
Calculer l'�ge de chacun de ces tufs et estimer l'�ge des ossements.
NAr(t)
/ NK(t) = 0,105 (elt-1) ; 2,26 10-11
/ (1,667 10-7) = 0,105 ( exp(5,81 10-11t)-1).
1,2912 10-3 = exp(5,81
10-11t)-1 ; exp(5,81
10-11t) =1,00129.
5,81
10-11t = ln(1,00129) =1,29 10-3 ; t = 2,22 107
ans.
NAr(t)
/ NK(t) = 0,105 (elt-1) ; 2,242 10-11
/ (2,604 10-7) = 0,105 ( exp(5,81 10-11t)-1).
8,610 10-5 = exp(5,81
10-11t)-1 ; exp(5,81
10-11t) =1,000086.
5,81
10-11t = ln(1,000086) =1,29 10-3 ; t = 1,48 106
ans.
|
Etude
d'une huile moteur.
Mesure de la viscosit� dynamique � l’aide d’un viscosim�tre � chute de bille.
Un
viscosim�tre � chute de bille comporte un long tube, mobile autour d’un
axe horizontal. Le tube comporte deux traits rep�res a et b. La
distance entre ces deux rep�res est not�e d. On y introduit de l’huile
de masse volumique r et une bille en acier de masse volumique rs
et de rayon calibr� R tel que son diam�tre soit inf�rieur au diam�tre
du tube. On rappelle que le volume V d’une sph�re de rayon R s’exprime
par la relation : V =4/3 pR3.
Le tube est muni d’une double enveloppe transparente dans laquelle circule de l’eau provenant d’un bain thermostat�.
On rappelle la loi de Stokes
pour une bille de rayon R en mouvement � la vitesse v dans un fluide de
viscosit� dynamique h : la force de frottement est oppos�e � la vitesse
et son expression est :
f = 6phRv
D�terminer l’unit� de la viscosit� dynamique � l’aide de la loi de Stokes.
h = f /(6pRv).
6 p est sans dimension ; R est une longueur (L) ; v est une vitesse, c'est � dire une longueur divis�e par un temps ( LT-1) ; f est une force soit une masse multipli�e par une acc�l�ration ( MLT-2).
Par suite [h]=MLT-2 / (L2T-1) =ML-1T-1 . ( kg m-1s-1 ou Pa s).
Reproduire le sch�ma simplifi� du tube central sur la copie, repr�senter les forces qui s’exercent sur la bille et les nommer.
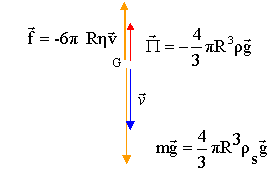
La bille est soumise
� son poids, � la pouss�e d'Archim�de P et � la force de frottement fluide. Expliquer qualitativement pourquoi la bille atteint une vitesse limite.
V�rifier que cette vitesse limite a pour expression : vlim=2/9R2g(rs-r)/ h.
La pouss�e d'Archim�de et le poids restent constants, tandis que le force de frottement fluide cro�t avec la vitesse.
La bille est
pseudo-isol�e lorsque la vitesse limite est atteinte : la somme des
forces est nulle.
4/3pR3rsg = 4/3pR3rg
+ 6pRhvlim.
4/3R2rsg - 4/3R2rg
= 6hvlim ; vlim=
4/3R2g(rs-r)/ ( 6h)=2/9R2g(rs-r)/ h.
Dans
les conditions de l’exp�rience, la bille, l�ch�e au-dessus du rep�re, a
atteint sa vitesse limite d�s le d�but du mouvement, avant d’atteindre
le rep�re a.
Exprimer la vitesse limite de la bille en fonction de d et de Δt, dur�e de parcours entre les deux rep�res a et b. vlim = d/Dt.
Montrer alors que la viscosit� dynamique peut s’�crire sous la forme : h =K(rs-r) Dt.
2/9R2g(rs-r)/ h= d/Dt ; h= 2/9R2g/ d (rs-r) Dt = K(rs-r)) Dt.
K = 2/9R2g/ d.
A 20 �C, on a mesur� une dur�e de chute Δt = 6,7 s et une masse volumique pour l’huile r = 875 kg.m-3.
Calculer la viscosit� dynamique de l’huile � cette temp�rature.
On donne K= 3,55 10-8 Pa m3 kg-1 et rs =7,85 103 kg m-3.
h=3,55 10-8( 7,85 103-875)*6,7 =1,66 10-3 Pa s.
|
|
|
