Mathématiques. Concours externe TSPEI 2019.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

.. ..
.
.

......


.....

Premier exercice.
Soit f la fonction définie pour tout réel x par f(x) = ex (ex-2).
1. a. Calculer f(0) puis f(ln2).
f(0) = e0(e0-2) = 1 (1-2) = -1.
f(ln2) =eln2(eln2-2) = 2 (2-2) = 0
b. Déterminer la limite de f en moins l'infini. Interpréter le résultat.
Les termes ex tendent vers zéro et f tend vers 0.
La droite d'équation y = -2 est asymptote à la courbe représentative de f.
 c. Déterminer la limite de f en moins l'infini.
Les termes ex tendent vers plus l'infini et f tend vers plus l'infini.
2. Déterminer la dérivée de la fonction f.
On pose u = ex et v = ex-2; u'=ex ; v' = ex.
f ' = u'v + v'u = ex (ex-2) + ex ex =2ex ( ex-1).
La dérivée s'annule pour ex-1 =0 soit x = 0.
La dérivée est positive pour x > 0  et f est croissante.
La dérivée est négative pour x < 0 et f est décroissante.
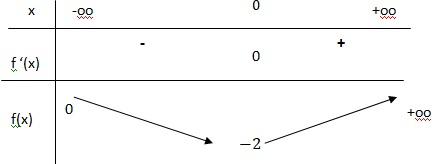
3. En déduire le tableau de variation de f.
 

4. Ecrire une équation de la tangente T à la courbe C au point d'abscisse x = ln2.
Coefficient directeur de la tangente = f '(ln2) =2 *2 (2-1) = 4.
Equation de T : y = 4 x +b.
La tangente passe au point de coordonnées ( ln2 ; f (ln(2) =0 ).
0 = 4 ln2 +b ; b = -4ln2.
y = 4x-4ln2.
 5. Construire la courbe C et la tangent T.

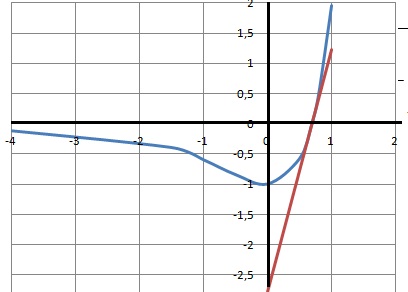6. Déterminer graphiquement, en fonction du réel m, le nombre de solutions de l'équation e2x-2ex-m=0.
f(x) -m = 0 soit f(x) = m.
m > 0 : une seule solution.
0 < m < -1 : 2 solutions.
m = -1 :une solution.
m < -1 : aucune solution.
7. Résoudre dans R l'inéquation : e2x-2ex-3 < 0.
On pose X = ex positif ou nul.
X2 -2X-3 = 0. Discriminant D = 4-4*(-3) = 16.
Solution retenue : X =(2+4) / 2 = 3.
3 = ex ; x = ln(3).
Solutions de l'inéquation : x appartient à ] -oo ; ln(3)].

...


....

 Deuxième exercice.
Une entreprise qui fabrique des disques durs pour ordinateurs dispose de deux sites de production A et B. A fabrique 80 % des disques dont 1 % sont défectueux et B en fabrique 20 % dont 2 % sont défectueux. On prélève au hasard un disque de l'ensemble de la production.
On considère les événements :
A : " le disque provient de A"
B : " le disque provient de B"
D :" le disque est défectueux".
1. Déterminer les probabilités suivantes. P(A), P(B), PA(D) et PB(D).
P(A) = 0,80 ; P(B) = 0,20 ; PA(D)=0,01 ; PB(D) =0,02.
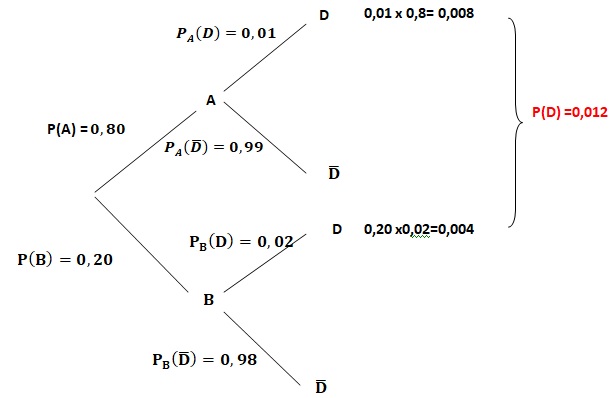
2. Calculer la probabilité que le disque soit défectueux.
Formule des probabilités totales. Voir ci-dessous.
 
3. Calculer la probabilité que le disque provienne de A sachant qu'il est défectueux.
PD(A) =P(A n D) / P(D) =0,008 / 0,012 =2 /3 ~0,0667.
4. Soit n un entier naturel non nul. Un client reçoit un lot de n disques durs. Calculer en fonction de n la probabilité qu'il reçoive :
a. Au moins un disque défectueux.
b. Exactement un disque défectueux.
On définit une variable aléatoire X qui à chaque lot de n disques durs associe le nombre de disques défectueux.
X suit une loi binomiale de paramètre n et p = 0,012.
Probabilité que tous les disques soient bons : P(X = 0) = (1-0,012)n = 0,988n.
Probabilité qu'il y ait au moins un disque défectueux : P(X > 1) = 1 -P(X=0) = 1-0,988n.
P(X = 1) = C1n x 0,988n x 0,012.

 

Troisième exercice.
1. Résoudre dans C l'équation (E1) z2-2z+2=0.
Discriminant D =(-2)2 -4*2 = -4 = 4 i2.
z1 = (2+2i) / 2 = 1+i.
z2 = (2-2i) / 2 = 1-i.
2. Déterminer le module et l'argument de chaque solution.
z1 et z2 étant conjugués, ils ont le même module et des arguments opposés.
|z1| =(12 +12)½ = 2½.
z1 / |z1| = 2½ / 2 +i 2½ / 2 = cos (p/4) + i sin (p/4)  ; z1 = 2½(cos (p/4) + i sin (p/4) = ; argument : p/4.
z2 = 2½(cos (-p/4) + i sin (-p/4) = ; argument : -p/4.

On veut résoudre dans C l'équation : (E2) z3-(2+i)z2+2(1+i) z-2i = 0.
3. Déterminer la solution de (E2) qui s'écrit sous la forme z = a i avec a un réel.
4. En déduire toutes les solutions de (E2).
a3i3 -(2+i)a2i2+2(1+i)ai -2i =0.
-a3i +(2+i)a2+2(1+i)ai -2i =0.
-a3i +2a2+ia2+2ai -2a-2i =0.
2a2-2a = 0 soit a =1.
i(-a3 +a2+2a-2)=0; a = 1. Soit z = i.
(z-i) ( z2 +bz +c) = 0.
On développe : z3+bz2+cz -iz2-ibz-ic =0.
z3+(b-i)z2+(c-ib)z -ic =0.
On identifie : c = 2 et b = -2.
Les solutions de  z2 -2z +2=0 sont z1 et z2 ( voir question 1).



  

menu