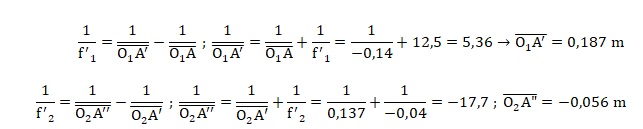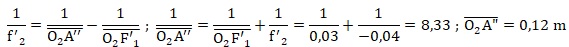Physique : t�l�objectif, chute d'une goutte, turbine � gaz.  Concours externe TSPEI 2019. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicit�s adapt�es � vos centres d’int�r�ts. .. .. . . ...... ..... Optique. Image d'un objet par une lentille convergente. Une lentille convergente L1 de centre optique O1 a une distance focale f '1 = +8,0 cm. Un objet AB vertical de hauteur 0,5 cm situ� � p1 = mesure alg�brique OA = -14,0 cm de la lentille. 1. a. D�terminer la vergence C1 de cette lentille. C1 = 1 /f '1 = 1 /0,08 =12,5 dioptries. 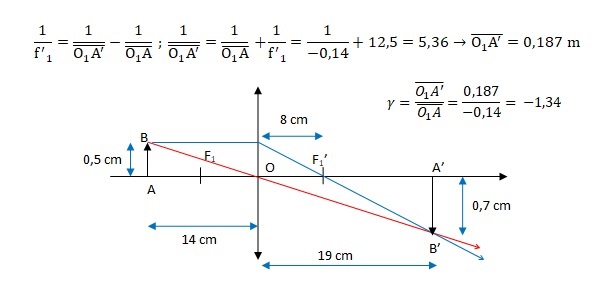1.b. Placer les foyers objet et image F1 et F'1 et construire l'image A'B' de AB. 1.c. D�terminer graphiquement O1A' et A'B'. 1.d. Retrouver ces valeurs par le calcul. 1.e. Calculer le grandissement de ce syst�me. T�l�objectif. Pour constituer un t�l�objectif, on associe sur le m�me axe optique la lentille L1, avec une lentille mince divergente L2, de centre optique O2 et de distance focale f '2 = -4,0 cm. Mesure alg�brique O1O2 = e = 5,0 cm. 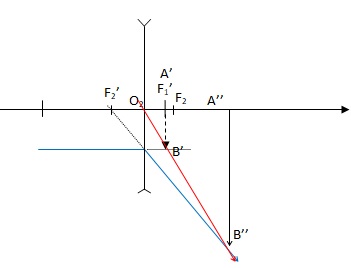1.2.a. Faire un sch�ma de la situation. 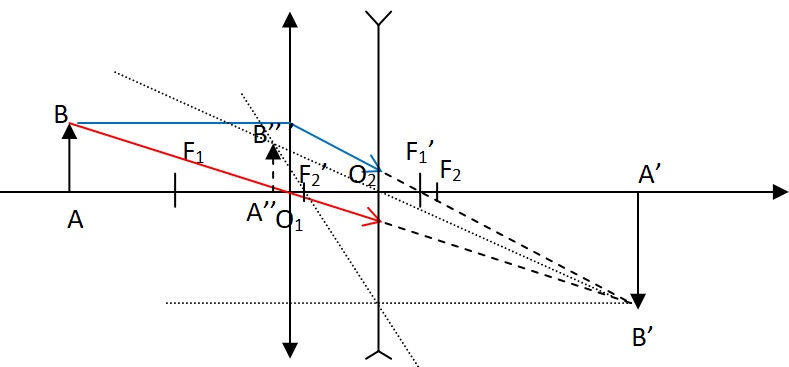1.2.b D�finir le foyer image d'un syst�me optique. Les rayons lumineux issus d'un objet � l'infini converge, apr�s travers�e du syst�me, en un point appel� foyer image. Cette combinaison peut �tre consid�r�e comme un syst�me optique unique poss�dant deux foyers F et F' appel�s foyers r�sultants, de distance focale f ' = - f '1 f '2 /(e-f '1- f '2). 1.2.c. En utilisant les relations de conjugaison des deux lentilles, exprimer O2F ' en fonction de f '1, f '2 et e. Calculer sa valeur. L'image interm�diaire A' B' sert d'objet virtuel pour la seconde lentille. 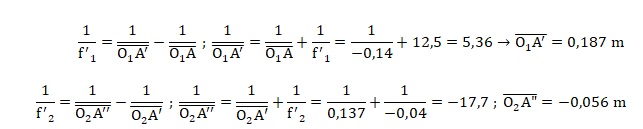1.2.d En d�duire l'encombrement total O1 F' du t�l�objectif. 1.2.e. Calculer f '. f ' = -8,0 x (-4,0) / (5,0 -8,0 +4,0)= 32 cm. 1.2.f. Quel est l'avantage d'un t�l�objectif par rapport � une distance focale f '. Moindre encombrement. A l'aide d 'une lentille unique, la distance capteur - lentille serait de 32 cm. On d�sire prendre une photo d'un immeuble de 20 m de haut situ� � 500 m de L1. On suppose que l'image se forme dans le plan focal de L1. 1.2.g. D�terminer la taille A'B' de l'image interm�diaire, puis la taille A"B" de l'image d�finitive. 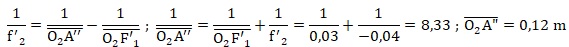|g1 |=0,08 / 500 =1,6 10-4 ; taille de A'B' : 20 x1,6 10-4 =3,2 10-3 m = 3,2 mm. |g2 |=0,12 / 0,03 =4 ; taille de A''B'' : 3,2 x4 =12,8 mm. ... .... Mesure de la charge d'un ion. On fait tomber  dans une atmosph�re gazeuse, entre les armatures d'un condensateur plan, des petites gouttes de glyc�rine de masse m. Le mouvement vertical de ces gouttes est observ� au microscope. Elles sont soumises � une force r�sistante de norme f =6 p h R v o� R est le rayon de la goutte, h la viscosit� du milieu et v la vitesse de la goutte. l'axe vertical d'�tude est orient� vers le bas. A l'insatnt initial, la goutte est l�ch� du ppoint O sans vitesse initiale. R = 2,0 �m ; h = 2,0 10-5 Pa s ; g = 9,8 m s-2. Masse volumique de la glyc�rine r = 1,25 103 kg m-3. On n�gligera la pouss�e d'Archim�de. Partie 1.  Condensateur non charg�. 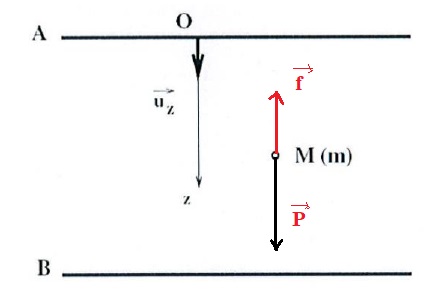1.a Faire l'inventaire des forces exerc�es sur la goutte et les repr�senter. La goutte est soumise � son poids et � la force de frottement. 1.b. Etablir l'�quation du mouvement de M en fonction de la vitesse. Ecrire la seconde loi de Newton sur l'axe Oz. m dv /dt = mg-f ; m dv /dt = mg -6 p h R v. dv /dt +6 p h R  / m v = g. 1.c. En supposant que v =A e-at +2gR2r / (9 h) est solution de l'�quation diff�rentielle, exprimer a en fonction de R, h et r. Pr�ciser son unit�. at est sans dimension, a est l'inverse d'un temps. Les solutions d'une �quation diff�rentielle du type y' + by=0 sont de la forme y = B e-bx. a = 6 p h R  / m avec m = 4/3 pR3 r. a = 9  h   / (2R2 r). 1.d. A partir des conditions initiales donner l'expression de A. La vitesse initiale est nulle : 0 = A +2gR2r / (9 h) ; A = -2gR2r / (9 h). 1.e. Donner l'expression et calculer la vitesse limite vlim. dvlim /dt = 0 ; 6 p h R  / m vlim = g. vlim = mg / (6 p h R). m = 4/3 pR3 r. vlim = 2g R2 r / (9 h) =2 x9,8 x (2,0 10-6)2x1,25 103 / (9 x2,0 10-5)=5,4 10-4 m / s. Condensateur charg�. On charge le condensateur en lui appliquant une tension U entre les armatures distantes de d. Puis on ionise les gouttes en faisant passer un faisceau de rayons X entre les plaques. Pour une tension U = VA-VB n�gative, l'exp�rimentateur observe une goutte immobile. U = -25 kV et d = 2,0 cm. 2.a Indiquer le sens du champ �lectrique E ainsi que la force F�l. 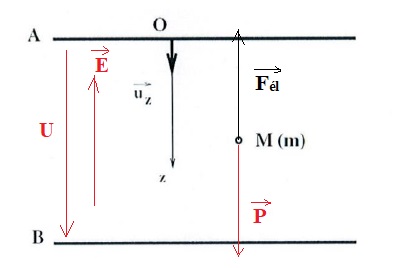2.b. Faire l'inventaire des forces exerc�es sur la goutte puis exprimer la charge q de la goutte en fonction de m, g, d et U. La goutte est soumise � son poids, � la force de frottement, n�gligeable dans ce cas, et � la force �lectrique. La somme de ces deux vecteurs forces est nulle : mg =F�l ;  mg = qE = q|U| / d. q = mgd / |U|. 2.c. Calculer q. Que remarque -t-on ? m =4/3 pR3 r=4 / 3 x3,14 x(2,0 10-6)3 x1,25 103 =4,2 10-14 kg. q = 4,2 10-14 x9,8 x0,02 /(2,5 104) =3,2 10-19 C, soit 2 fois la charge �l�mentaire e.   Turbine � gaz � combustion interne. Le principe est le m�me que celui d'une machine � vapeur, sauf qu'au lieu d'entrainer un piston, le fluide sous pression entraine une turbine. Le gaz assimil� � un gaz parfait d�crit le cycle suivant : - initialement � l'�tat 1, pression P1 et temp�rature T1, il subit une compression adiabatique r�versible jusqu'� l'�tat 2, pression P2 et temp�rature T2. - un r�chauffement isobare au contact d'une source chaude jusqu'� l'�tat 3, pression P3 et temp�rature T3. - une d�tente adiabatique r�versible jusqu'� l'�tat 4, pression P4 et temp�rature T4. - refroidissement isobare au contact avec une source froide et retour � l'�tat 1. 1.a. Quelle est la relation entre P2 et P3 ? Le r�chauffement �tant isobare ( passage de l'�tat 2 � l'�tat 3), P3=P2. 1.b. Tracer l'allure du cycle par le gaz dans le diagramme P = f(V). 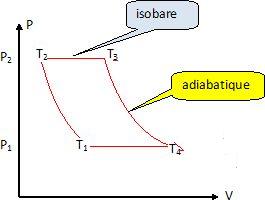2.a. Rappeler la loi de Laplace liant P, V et g pour une tranformation adiabatique r�versible pour un gaz parfait. P Vg = constante. 2.b. Montrer que cette loi peut s'�crire : P1-g Tg = constante. PV = nRT ; V = nRT / P ; P (nRT)g / Pg = P1-g Tg = constante. 2.c En d�duire les expressions de T2 en fonction de P1, P2, T1 et g  et celle de T3 en fonction de P1, P4, T4 et g. P11-g T1g = P21-g T2g ; T2g = ( P1/P2)1-g T1g  ; T2 =( P1/P2)(1-g) / g T1 . P31-g T3g = P41-g T4g ; T3g = ( P4/P3)1-g T4g  ; T3 =( P4/P3)(1-g) / g T4 . 3. Pour n = 1 mol de gaz parfait, exprimer en fonction de Cpm et des temp�ratures ad�quates : - Qc chaleur �chang�e avec la source chaude. - QF chaleur �chang�e avec la source froide. Qc = Cpm (T3-T2). QF = Cpm (T1-T4). 4. En utilisant le premier principe, exprimer Wcycle, le travail �chang� par mole de gaz avec l'ext�rieur au cours du cycle en fonction de Cpm et des 4 temp�ratures. La variation d'�nergie interne du gaz est nulle sur le cycle : Wcycle + QC +QF = 0. Wcycle  = - Cpm (T3-T2) -Cpm (T1-T4). 5. Exprimer le rendement th�orique en fonction des temp�rature. Rendement = valeur absolue du travail r�cup�r� / �nergie d�pens�e � la source chaude. |Wcycle | / Qc = 1-QF / QC = 1- (T1-T4) / (T2-T3). 6. On pose t = P2 / P1. Montrer que le rendement th�orique s'�crit : 1 -t (1-g) / g. T4  = T3 ( P3/P4)(1-g) / g  =T3 ( P2/ P1)(1-g) / g  =T3 t (1-g) / g. T1  = T2 ( P2/P1)(1-g) / g  =T2 t (1-g) / g. T1-T4 =(T2-T3) t (1-g) / g. Rendement : 1-t (1-g) / g. 7. Calculer le rendement pour les trois gas du tebleau ci-dessoupour t = 4,0. gaz argon air CO2 g 1,67 1,4 1,31 1/g-1 -0,401 -0,29 -0,24 si r = 4,0 : 1- r(1-g)/g 0,43 0,33 0,28 Le meilleur rendement est obtenu avec l'argon. 8. Pour le gaz poss�dant le meilleur rendement,  calculer T2 et T4. P1 = 1,0 105 Pa ; T1 = 300 K ; T3 = 900 K. T2 = T1 t (g-1) / g = 300 x 4,00,401 = 523 K. T4 = T3 t (1-g) / g = 900 x 4,0-0,401 = 516 K.

menu