Mathématiques,
probabilité, suite, concours Geipi polytech 2021.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
..
..
|
.
.
|
..
..
......
...
|
Exercice 2 (22 points).
soient A et B deux pièces de monaies. La pièce A donne "face" avec la
probabilité 0,5 et B donne "face" avec la probabilité 0,25. Lorsqu'on
lance l'une de ces pièces, si on obtient "face", on conserve cette
pièce pour le laner suivant, sinon on change de pièce.
A. Trois lancers successifs des pièces.
On commence par lancer la pièce A. On note Fi l'événement on obtient "face au i ème lancer".
1. Compléter l'arbre de probabilité.
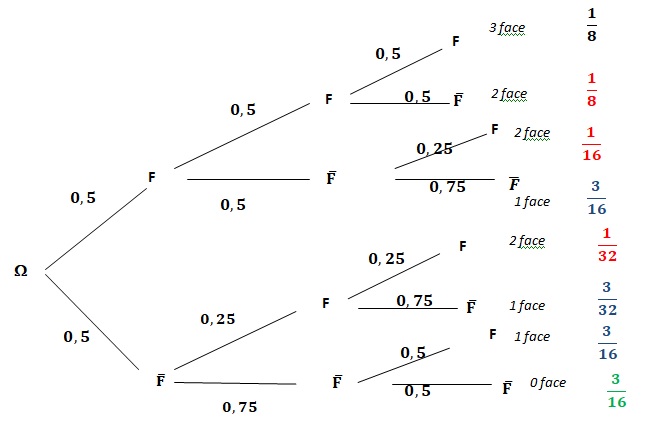
2. X
désigne la variable aléatoire donnant le nombre de fois où "face
" est obtenu. Compléter le tableau donnant la loi de probabilité
de X.
X
|
0
|
1
|
2
|
3
|
p(X)
|
3/16
|
15 / 32
|
7/32
|
1 / 8
|
3. Calculer l'espérance de X.
15 / 32 +2 x7 /32 +3 /8 =41 / 32.
B. Etude d'une suite.
On considère la suite (un) définie par : u0 =-1 et un+1 = -0,25 un +0,75.
4. Calculer u1 et u2.
u1 = -0,25 u0 +0,75=0,25+0,75=1.
u2 = -0,25 u1 +0,75= -0,25+0,75= 0,5.
5.a On considère la suite (vn) définie par : vn = un -0,6. Calculer v0.
v0 = u0 -0,6 = -1,6.
5.b. Montrer que (vn) est une suite géométrique de raison -0,25.
vn+1 = un+1 -0,6 = -0,25 un +0,75-0,6 = -0,25 un +0,15 =-0,25 un +0,25 x0,6.
vn+1 = -0,25(un-0,6)= -0,25 vn.
6. En déduire que un = -1,6(-0,25)n +0,6.
vn = v0(-0,25)n =-1,6 (-0,25)n ;
un = vn +0,6 = -1,6(-0,25)n +0,6.
7. Justifier que (un) converge vers 0,6.
-1 < -0,25 < 1 ; (-0,25)n tend vers zéro et un tend vers 0,6.
|
...
|
....
|
C. n lancers successifs des pièces.
On considère les événements suivants :
An : " on utilise la pièce A au n ème lancer".
non An : " on utilise la pièce B au n ème lancer".
On note pn = P(An). On commence toujours par lancer la pièce A et donc p1 = 1.
8. Donner PAn ( An+1) et P non An(An+1).
Probabilité d'obtenir "Face" en lançant la pièce A : PAn ( An+1) =0,5.
Probabilité d'obtenir "non Face" en lançant la pièce B :P non An(An+1)= 0,75.
9. Donner l'expression de P(non An), P(An+1 n An) et P(An+1 n non An).
P(non An)=1-P(An) = 1 -pn.
A n ème lancer on lance A et au n+1ème lancer, on lance A et on obtient Face : P(An+1 n An)=PAn ( An+1) x P(An)=0,5 pn.
A n ème lancer on lance B et au n+1ème lancer, on lance A et on obtient non Face : P(An+1 n non An)= P non An(An+1) x P(non An) =0,75 (1 -pn).
10. En déduire que pn+1=-1,6(-0,25)n +0,6.
pn+1=P(An+1)=P(An+1 n An)+P(An+1 n non An)=0,5 pn +0,75(1-pn) = -0,25 pn+0,75.
D'après la question 6, on a pn = -1,6 (-0,25)n +0,6.
11.a On note Fn l'événement "obtenir Face au nème lancer".
Donner l'expression de P(Fn n An) et P(Fn n non An) en fonction de pn.
P(Fn n An) = 0,5 pn ; P(Fn n non An) = 0,25(1-pn).
11.b. Déterminer la limite de P(Fn).
P(Fn) = P(Fn n An) +P(Fn n non An) =0,5 pn +0,25(1-pn) =0,5 pn + 0,25(1-pn) =0,25(1+pn).
Or pn tend vers 0,6 quand n tend vers plus l'infini.
P(Fn) tend vers 0,25 x(1+0,6) =0,4.
|
|