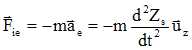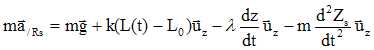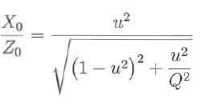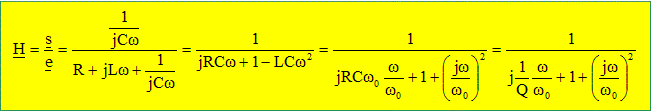Mécanique
et électronique : protection contre les séismes,
Concours ITPE 2020.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
..
..
|
|
......
.....
|
Réduction des oscillations propre du bâtiment.
Sous
l'action du vent ou d'un séisme, un immeuble oscille, un peu comme un
roseau. Ces ocillations risquent d'endommager la structure. On
s'intéresse à la tour Citicorp à New-York haute de 279 m pour 59
étages. En l'absence de dispositif adapté, la tour oscille avec une
pseudo-période de 6,5 s et l'amplitude de ces oscillations ne
diminue que de 5 % par cycle.
Le comportement est analogue à celui d'un oscillateur harmonique
amorti. L'équation différentielle du mouvement horizontal x du centre
de masse de la tour se met sous la forme :
x" +w0/ Q x'+w02 x = 0.
1. Quelles sont la signification et la dimension de Q et w0 ?
w0 : pulsation propre en rad / s.
Q : facteur de qualité sans dimension.
[w0 /Q x'] est homogène à une accélération et [x'] est homogène à une vitesse.
[w0 /Q) est donc homogène à l'inverse d'un temps ; w0 est la pulsation propre ( rad/s). Q est sans dimension.
2. On s'intéresse à l'action d'une rafale brutale qui communique à l'immeuble une vitesse initiale v0. Au vu des données, quelle est la nature du régime étudié ? Quelle inégalité vérifie Q ?
Oscillations libres amorties.
Equation caractéristique associée à x" + w0 /Q x' + w02 x =0 : r2 +w0 /Q r + w02=0.
Le discrimant D = (w0 /Q)2-4w02 doit être négatif. 1 / Q2-4 < 0 ; Q2 >0,25 ; Q >0,5.
3. On confond la pulsation propre et la pseudo-pulsation. A l'aide des données, déterminer w0.
w0 =2 p / T0 =2 p / 6,5 ~0,31 p ~ 0,97 rad / s.
4. Montrer que le facteur de qualité de la tour vérifie Q = -p / (ln(1-1 / 20)) ~ 20 p.
Dans le cas du régime pseudopériodique, les solutions de l'équation différentielle sont de la forme :
x (t)= A exp-(w0t / (2Q)) cos( wt+f).
L'amplitude des oscillations ne diminue que de 5 % par cycle : 1- 5 / 100 = 1-1 / 20.
exp-(w0T / (2Q))=1 -1 /20.
-w0T / (2Q)=ln(1-1 / 20) ; -p / Q = ln(1-1 / 20) ;
Q = -p / (ln(1-1 / 20)) ~ 20 p.
5. Quelle est la durée nécessaire pour que l'amplitude des oscillations atteigne 1 % de son amplitude initiale ?
A(nT) / A0 =0,01 ; à chaque cycle A(2T) = 0,95 A(T).
A(nT) = 0,95n A0. 0,95n =0,01. n ln(0,95) =ln(0,01) ; n ~ 89.
Durée nécessaire : 89 x 6,5 ~578 s ~6 min 38 s.
Pour
limiter les oscillations, on installe au sommet du gratte-ciel un
oscillateur résonant muni d'un dispositif d'amortissement : il s'agit
d'une masse de 400 t placée sur une couche dhuile et reliée aux
murs par des ressorts et des amortisseurs.
6. Grâce à ce dispositif, l'atténuation des oscillations est de 50 % par cycle. En déduire la nouvelle valeur de Q et commenter.
L'amplitude des oscillations diminue de 50 % par cycle : 1- 50 / 100 = 0,5.
Q = -p / ln(0,5) ~4,5.
Le retour de la tour à l'équilibre est plus rapide.
|
...
|
|
Sismographe.
Un
sismographe est un dispositif enregistrant les mouvements du sol. Une
station sismique doit comporter 3 sismographes, un vertical et
deux horizontaux. Les périodes des ondes sismiques varient sur une
large gamme, du dixième de seconde à plus de 1000 secondes.
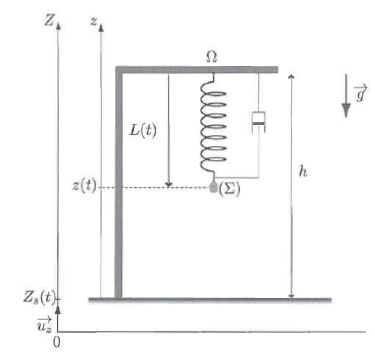
Le sismographe est constitué d'un solide de masse m suspendu à un ressort dont l'autre extrémité W
est liée à un bâti rigide solidaire du sol en vibration. Un dispositif
d'acquisition permet d'enregistrer le mouvement du solide par rapport
au bâti. On souhaite que ce mouvement reproduise le plus fidèlement
possible celui du sol par rapport au référentiel d'étude R supposé
galiléen. On appelle RS le référentiel lié au bâti rigide.
Le sol est supposé horizontal. Son mouvement vertical, lors d'une secousse sismique sinusoïdale de pulsation w, est repéré par la cote, mesurée par rapport à R :
Zs(t) = Z0 cos ( wt).
Le ressort de masse négligeable, de constante de raideur k, de longueur au repos L0,
a pour valeur L(t) à l'instant t. Un amortisseur relié au ressort,
exerce sur le solide une action mécanique modélisée par la force
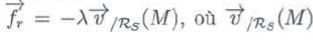 est la vitesse du solide dans le référentiel Rs. est la vitesse du solide dans le référentiel Rs.
On note L1 la longueur du ressort quand le solide est à l'équilibre en absence de secousse sismique. Le solide se situe à la cote z1 repérée par rapport au bati. La position du solide est repérée par x(t) = z(t) - z1.
8. Etablir l'équation différentielle vérifiée par x(t).
A l'équilibre le poids et la tension du ressort sont deux forces opposées : mg = k(L1-L0) avec L1 = h-z1.
z1 = h - L0-mg / k. (1)
Dans le référentiel non galiléen Rs, en translation par rapport au référentiel galiléen R, le solide S est soumis à une force d'inertie :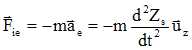
Ecrire la relation fondamentale de la dynamique apliquée au solide dans le référentiel lié au boîtier :
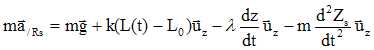
Zs(t) = Z0 cos ( wt) ; dZs(t) /dt = -wZ0 sin ( wt) ; d2Zs(t) /dt2 = -w2Z0 cos ( wt).
Projeter sur l'axe vertical : m z" = -mg +k(h-z-L0) -l z' + mw2Z0 cos ( wt).
Tenir compte de (1) : m z" = k(z1-z) -l z' + mw2Z0 cos ( wt).
Or : x(t) = z(t) - z1 d'où : x" + k/m x + l /m x' = w2Z0 cos ( wt).
En posant w02 =k/m et Q = mw0 / l = (km)½/ l : x" + w0 /Q x' + w02 x = w2Z0 cos ( wt). (2)
On cherche la réponse du sismographe sous la forme : x(t) = X0 cos ( wt+F). On pose u = w / w0.
10. Montrer que : 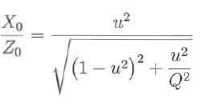
En notation complexe : x(t) =X0 exp (j F) ; x'(t) = jwX0 exp (j F) ; x"(t) = (jw)2X0 exp (j F)= -w2X0 exp (j F). Repport dans (2).
-w2X0 exp (j F) + w0 /Q jwX0 exp (j F) + w02 X0 exp (j F) = w2Z0.
Diviser par w02 : (-w2/ w02 +j w /(Qw0) +1) X0 exp (j F)= w2/ w02Z0.
(1-u2 + j u / Q) X0 exp (j F) = u2Z0.
Identifier les modules : ((1-u2)2 + u2/Q2)½ X0 = u2Z0 ; X0 /Z0 = u2/ ((1-u2)2 + u2/Q2)½.
Le graphe représentant X0 /Z0 en fonction de u, pour différentes valeurs du paramètre Q est donné :
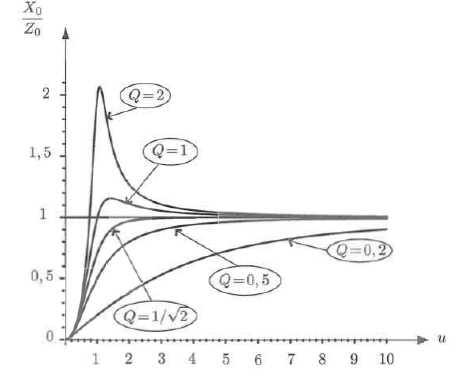
11. Vérifier
que l'allure de ce graphe est compatible, à haute et basse fréquence,
avec l'expression calculée.
A haute fréquence, u tend vers l'infini et X0 /Z0 tend vers 1. A basse fréquence, u tend vers 0 et X0 /Z0 tend vers zéro.
On pose Y = (Z0/X0)2 et x = 1/u.
12. Montrer qu'il ne peut pas y avoir de résonance si Q est inférieur à une valeur limite Q0 à déterminer.
((1-u2)2 + u2/Q2 ) / u4 = Y ; Y = (1-1/u2)2 + 1/(Qu)2 ; Y = (1-x2)2 + x2/Q2 ;
Dériver Y par rapport à x et chercher la valeur de x qui annule cette dérivée :Y ' = -4x(1-x2) +2x/Q2 =0.
x = 0 et -2(1-x2) +1/Q2 =0 ; x = (1-1/(2Q2))½. 1-1/(2Q2) doit être positif ou nul : 1-1/(2Q2) >=0 ; Q =Q0 >= 1 / 2½.
Pour x = 0, Y = 1 ; pour x très grand Y tend vers l'infini ; pour Q =Q0 , Y présente un minimum et par suite X0 /Z0 présente un maximum ( résonance ).
Il ne peut pas y avoir de résonance si Q < Q0.
13. Comment faut-il choisir w0 par rapport à w de la secousse sismique ? Justifier.
Le mouvement du solide doit restituer le mouvement du sol : X0 = Z0 : u = w / w0 soit w >> w0.
Quel est le meilleur choix pour le paramètre Q, en termes de fidélité de la réponse et de durée du rgime transitoire ?
Pour Q = Q0, X0 /Z0 tend rapidement vers 1 pour u = 3 et de plus la durée de l'amortissement est faible.
Quel
est l'ordre de grandeur de l'allongement du ressort à l'équilibre
d'un sismographe optimisé pour détecté des ondes sismiques dont la
période est une seconde ? Commenter.
Léq-L0 = mg / k avc w02 = k / m ; Léq-L0 = g / w02 = 9,8 / (4p2)~0,25 m pour une fréquence f = 1 Hz.
Léq-L0 =9*9,8 / (4p2 )~2,2 m pour une fréquence f = 3 Hz.
Un sismographe de ce type doit avoir de très grandes dimensions.
|
....
|
Filtrage du signal en sortie du sismographe.
Le
signal en sortie du sismographe est souvent parasité par un bruit haute
fréquence. On cherche à éliminer les parasites en utilisant un filtre
passif constitué d'un circuit RLC série.
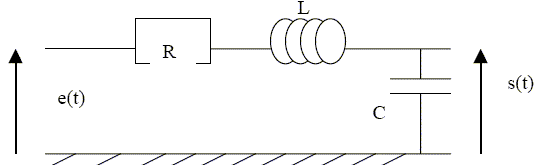
Il est soumis à une tension d'entrée
sinusoidale e(t)=U0 cos(wt).
On note s(t) la tension de sortie.
14. Montrer que s(t) vérifie l'équation :
s''(t)+ w0/Q s'(t) +w02 s(t) = w02 e(t) avec w02 =1 / (LC) et w0/Q = R / L.
Additivité des tensions :
e(t) = R i + Ldi /dt +s(t) avec i = C ds(t) / dt = Cs'(t) ; di/dt =C s"(t).
e(t) = RC s'(t) +LC s"(t) +s(t).
e(t) / LC = R / L s'(t) +s"(t) +s(t) / (LC).
w02 e(t) =s''(t)+ w0/Q s'(t) +w02 s(t).
On se place en régime permanent : on cherche s(t) =um cos ( wt+F).
On utilise la notation complexe : e(t)=U0 exp(jwt) ; s(t)=um exp(jwt) ; um =umexp(jF).
15. Déterminer le circuit équivalent à haute et basse fréquence. En déduire la nature de ce filtre.
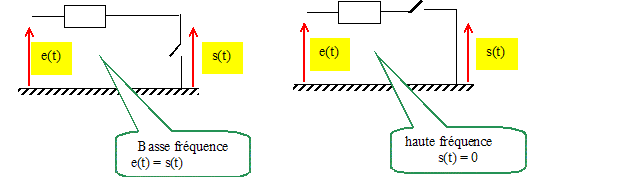
Le filtre coupe les hautes fréquences, mais laisse
passer les basses fréquences : filtre passe bas.
16. Montrer que :
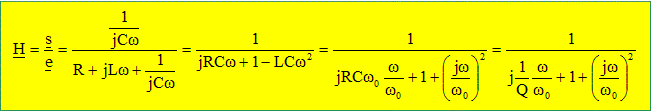
Le dénominateur compte un terme en w2
: donc filtre d'ordre 2.
17. On donne l'allure du diagramme de Bode pour H. Justifier que f0 = w0 / 2p = 1 kHz.
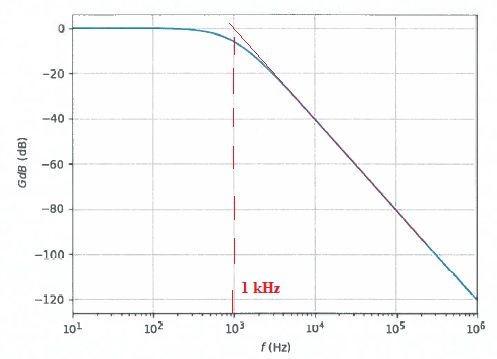
On appelle gain, la fonction , telle que
GdB= 20 log H .
18. Donner les équations des
asymptotes de GdB aux basses fréquences et
aux hautes fréquences.
On pose x = w / w0.
H = 1/ (jx / Q +1-x2) = [(1-x2)-jx/Q ] / [(1-x2)2+Q-2x2
].
H =[(1-x2)2+Q-2x2
]-½.
GdB= -10 log
[(1-x2)2+Q-2x2
]
si x tend vers 0, alors GdB est
équivalent à 0. L'axe des abscisses est
asymptote horizontale.
si x tend vers l'infini, alors GdB est
équivalent à -40 log x. ( droite de pente -40
dB par décade).
Cette droite asymptote coupe l'axe des abscisses en
x=1. |
19. Déterminer les valeurs limites de la phase à basse et haute fréquence. Vérifier la cohérence avec le diagramme suivant.
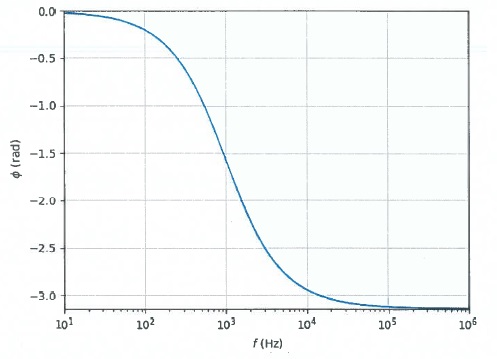
Argument de H : tan F = -x / [Q(1-x2)].
Recherche des asymptotes :
lorsque x tend vers 0+, F
tend vers 0-: l'axe des abscisses est
asymptote.
lorsque x tend vers l'infini, F
tend vers -p+
: la droite F=
-P est
asymptote.
valeur particulière F(1)
= -½ p .
Le filtre est un filtre passe bas d'ordre 2.
20. En réalité, le signal d'entrée s'écrit e(t) = U1 cos (w1t) +U2 cos (w2t) avec f1 = w1 / (2p) = 100 Hz et f2 = w2
/ (2p) = 20 kHz. Quel est sans calcul l'allure du signal de sortie ? On
précisera en particulier sa fréquence et son amplitude.
Le filtre est un filtre passe bas d'ordre 2. Seul le signal de fréquence f1 = 100 Hz est obtenu en sortie.
Le gain est égal à zéro : H = 1 ; l'amplitude du signal de sortie est égale à celle du signal d'entrée soit U1.
|
|
|

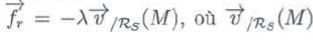 est la vitesse du solide dans le référentiel Rs.
est la vitesse du solide dans le référentiel Rs.