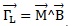Montagnes
russes, moteur asynchrone, looping.
Concours ITPE 2021.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
..
..
|
|
......
.....
|
Remontée
des wagons.
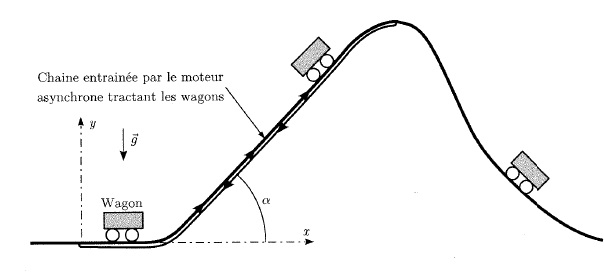
a =
45° ; hauteur maximale H ; m : masse d'un wagon.
1.a.
Moteur asynchrone.
Le stator ( non étudié ici ) permet de générer
le champ magnétique supposé uniforme B0 et tournant à la
vitesse angulaire w.
Le rotor est modélisé par une bobine plate constituée de N spires
traversées par un courant électrique induit d'intensité i(t).
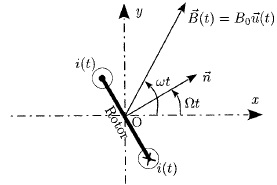
Les spires sont supposées confondues, circulaires, de section S. La
vitesse de rotation du rotor W
est supposée constante.
La résistance électrique du rotor est R et son inductance L.
Le rotor subit l'action motrice des forces de Laplace dont le moment en
O est 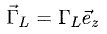 ainsi que l'action résistive
permettant d''entrainer la chaîne et les wagons dont le moment en O est ainsi que l'action résistive
permettant d''entrainer la chaîne et les wagons dont le moment en O est
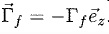 . .
1. Déterminer le
flux du champ magnétique F
engendré par le stator à travers le rotor en fonction de B0,
S, N, W, w et t.
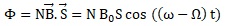
2.
En Déduire l'expression de la force électromotrice e induite dans
le rotor en fonction de
B0, S, N, W,
w et t.
e = -dF /dt = N B0
S (w-W) sin((w-W)t).
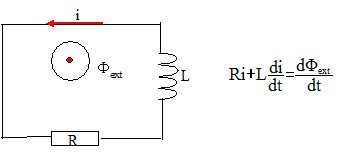
3. Proposer un
schéma électrique équivalent du rotor et en déduire que le courant
électrique i(t) vérifie l'équation différentielle suivante : Ldi/dt +Ri
= F0 wg sin(wgt) où wg = w-W, vitesse angulaire de glissement et F0 = NSB0.
4.
On cherche la solution de cette équation différentielle en notation
complexe sous la forme i
= I exp(j(wgt+f). Déterminer les
expressions de I et f en fonction de R, L,wg et F0.
di/dt = j I wg exp(j(wgt+f).
L'équation différentielle s'écrit : j L I wg exp(j(wgt+f)+ R I exp(j(wgt+f) = F0 wg exp(jwgt).
j
L I wg exp(jf)+ R I
exp(jf) = F0 wg .
(j Lwg +R)
I exp(jf) = F0 wg .
Egaler les modules : (R2 +(Lwg)2)½ I= F0 wg . I = F0 wg / (R2
+(Lwg)2)½.
Egaler les arguments : f
=- tan-1(Lwg /R).
5. Quel est le
moment magnétique associé au rotor ?
i(t) = F0 wg / |Z|
sin (wgt+f).
Moment magnétique d'une spire orienté suivant l'axe perpendiculaire à
la spire :
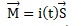 ; M = i(t) S = F0 wg S / |Z|
sin (wgt+f). ; M = i(t) S = F0 wg S / |Z|
sin (wgt+f).
6. En déduire
l'expression du moment en O des forces de Laplace exercé sur le rotor.
Montrer que sa valeur moyenne est :
< GL>
= F20 wg R / (2((R2 +(Lwg)2)).
Ce moment magnétique est soumis à un couple mécanique dont le moment
par rapport à l'axe vaut : 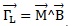
GL
= F20 wg / |Z|sin (wgt+f). sin (wgt).
avec sin (wgt+f). sin (wgt) = ½ [cos (f)- cos(2wgt+f)]
GL
= F20 wg / (2|Z|)[cos
(f)-
cos(2wgt+f)].
La valeur moyenne de cos(2wgt+f) est nulle et cos (f) = R /|Z|.
<
GL> = F20 wg R / (2((R2 +(Lwg)2)).
La figure suivante donne la représentation graphique de <
GL> en
fonction de la vitesse de rotation du rotor W dans le cas ou w = 100 rad /s.
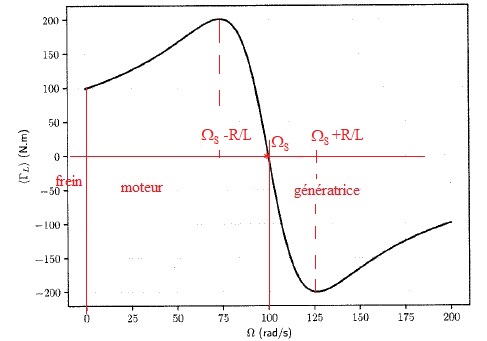
7. Quel domaine de
vitesse de rotation du rotor W
correspond à un fonctionnement moteur de cette machile asynchrone ?
Estimer le couple moteur Gmax.
<
GL>
doit être positif pour un fonctionnement moteur : W
inférieur à 100 rad /s. Gmax
=200 N m.
8. Pour un couple
résistant Gf
appartenant à [G0,
Gmax[
constant, justifier que le rotor peut tourner à vitesse constante pour
deux valeurs W1
et W2
> W1.
Que représente G0
? Déterminer sa valeur. Comment obtenir graphiquement W1 et W2.
Couple de démarrage G0 ~100 N m.
Pour R petit, la
zone WS-R/L
< W < WS+R/L
peut être modélisée par une droite ; cela permet d'avoir une vitesse de
rotation constante ( stabilité ) quelques soient les variations du
couple de charge.
9. Etudier dans le domaine Gf appartenant à [G0, Gmax[ la
stabilité des rotations W1 et W2. On pourra raisonner sur l'évolution de G au voisinage de W1
et W2.
10. Que se passe
t-il si Gf >
Gmax
? Arrêt du moteur.
11. Que se passe t-il si Gf appartient à
[0 ; G0]
?
12. A quelle
condition sur Gf
le moteur peut-il démarrer ? Le couple de démarrage G0 n'est pas nul, une machine asynchrone est
capable de démarer seule.
Vitesse d'ascension du wagon.
La chaîne
tractant les wagons est entrainée par le moteur précédent. On admet que
la relation entre la vitesse de montée du wagon v et la vitesse de
rotation du moteur : v = k W
où k = m /30. On néglige toute perte d'énergie par frottements.
13.
Déterminer l'expression de la force qu'exerce la
chaine sur le wagon de vitesse v constante en fonction de m, g et
a.
Le wagon est soumis à son poids, verticale vers le bas, valeur mg, à
l'action du plan perpendiculaire au plan et à l'action de la chaine,
parallèle au plan, vers le haut du plan. La vitesse étant constante, la
somme vectorielle des forces est nulle.
Projection
de la somme vectorielle des forces sur un axe parallèle au plan : mg
sin a = F.
14. Exprimer la
puissance reçue par le wagon de la part de l'ensemble {chaine +
moteur} en fonction de m, g, a,
k et W. En
déduire une expression du couple résistif Gf.
Puissance reçue= force fois vitesse = mg kW sin a .
A vitesse constante la puiisance reçue est égal à la puissance du
couple résistif.
Couple résistif= puissance / vitesse de rotation = mg k sin a .
15.
Déterminer la masse maximale du wagon pouvant être tracté sur une pente
d'angle a =
45°. Quelle est alors sa vitesse ?
Couple
résistif=m g m / 30 sin 45 = m2
x9,8 *sin(45) / 30 ~0,231 m2.
Couple moteur maxi =200 Nm ; 0,231 m2 =200 ; m = 29,4 kg.
W =75
rad / s ; v = k W
= m / 30 W =29,4 / 30 x75 =73,5 m /s.
16.
Quelle vitesse maximale ne peut dépasser un wagon plus léger ?
Wmax
= 100 rad /s ; v max =k Wmax= m / 30 Wmax =10 m /3.
|
...
|
|
|
....
|
Looping.
On s'interesse à la descente et à la possibilité de faire un looping.
On cherche la hauteur H minimale permettant la russite d'un looping
circulaire de centre O, de rayon a et de hauteur h = 2a.
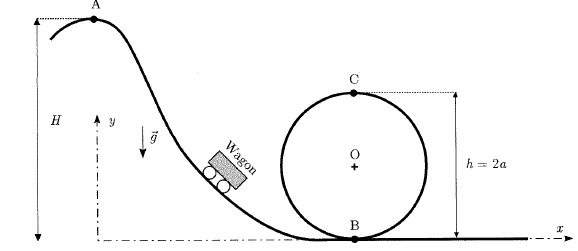
On modélise le wagon par un point matériel P glissant sans frottement
sur les rails. Initialement le wagon part du point A, d'altitude H à
vitesse négligeable.
17. Déterminer la vitesse vB au point B en fonction de g et H.
Conservation de l'énergie mécanique.
En A, EM = mg H ; en B, origine des altitudes, EM = ½mv2B.
½mv2B = mgH ; vB = (2gH)½.
18. En supposant que le wagon ne peut rompre le contact avec les rails, déterminer la vitesse vC
au point C et trouver une condition reliant h et H nécessaire pour que
le wagon puisse atteindre C. Cette condition sera valide par la suite.
Energie mécanique en C : 2 mg a+½mv2C ;
Conservation de l'énergie mécanique entre A et C : 2mga+½mv2C =mgH ;
v2C =2g(H-2a) ; vC =(2g(H-2a))½.
On peut atteindre C avec une vitesse vC =0 ; soit H = 2a= h.
Dans certains manège, le wagon n'est pas attaché au rails mais juste
posé dessus. Il faut éviter que le wagon ne rompe le contact avec les
rails.
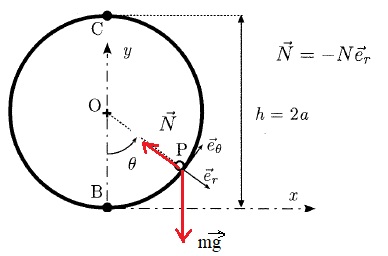
19. Déterminer l'expression de la vitesse v(q) de P en fonction de g, H, a et q.
Conservation de l'énergie mécanique entre A et P :
mgH =½mv2P +mga(1-cos(q)).
v2P =2gH -2ga(1-cos(q)).
20. Démontrer l'expression ci-dessous.
N = mg(2H/a +3 cos q-2).
Relation fondamental de la dynamique en projection sur l'axe OP :
-N +mgcos(q) = -mv2P / a ; N =mgcos(q) +mv2P / a ;
N =mgcos(q)+2mgH /a -2mg(1-cos(q)).
N = mg[2H /a +3cos(q)-2].
21. En déduire la condition limite de décollage.
Lorsque N s'annule, le wagon décolle : 2H /a +3cos(q)-2 =0.
22. On souhaite éviter qu'un tel décollage intervienne lors du looping. En déduire la hauteur minimale Hmini que doit dépasser H afin de réussir le looping.
2Hmini /a =2-3cos(q) avec q = p.
2Hmini /a =5 ; Hmini =2,5 a.
|
|


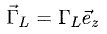 ainsi que l'action résistive
permettant d''entrainer la chaîne et les wagons dont le moment en O est
ainsi que l'action résistive
permettant d''entrainer la chaîne et les wagons dont le moment en O est
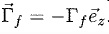 .
.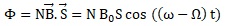

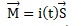 ; M = i(t) S =
; M = i(t) S =