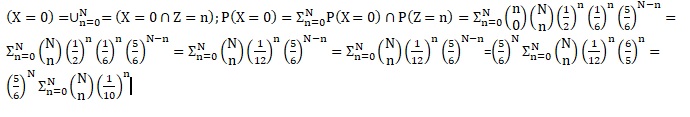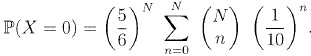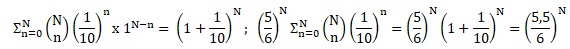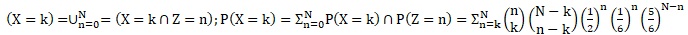Probabilités.
Concours ITPE 2021.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
..
..
|
|
......
.....
|
On
dispose d'un dé équilibré à 6 faces et d'une pièce non truquée.
Soit N un entier naturel non nul fixé. On effectue N lancers du dé. On
lance ensuite une pièce de monaie autant de fois que l'on a
obtenu de "6" au cours des N lancers du dé. On définit alors les
trois variables aléatoires X, Y et Z par :
Z désigne le nombre de 6 obtenus au cours des N lancers.
X désigne le nombre de pile obtenus lors de tous les lancers de la pièce.
Y désigne le nombre de face obtenus lors de tous les lancers de la pièce.
1. Déterminer la loi de Z, son espérance et sa variance.
Chaque lancer du dé est une expérience de Bernoulli ; le
succés est d'obtenir 6 ; sa probabilité est p = 1 /6 = constante.
Z suit la loi de Bernoulli B (N ; 1 /6).
P(Z = k) = CkN (1/6)k (5/6)N-k.
Espérance E(Z) = N / 6 ; variance V(Z) =N x1 /6 x5 /6 = 5 N / 36.
2. Déterminer la relation entre X, Y et Z.
Z = nombre de lancers de la pièce = nombre de pile + nombre de face.
Z = X+Y.
3. Soient deux entiers k et n tous les deux inférieurs ou égaux à N.
a. Donner la valeur de PZ=n(X=k) si k > n et expliquer pourquoi en une phrase.
On a obtenu n fois le nombre 6 ; on lance n fois la pièce ; on peut obtenir au mieux un nombre de pile inférieur ou égal à n.
PZ=n(X=k) =0 si k > n.
b. Expliquer pourquoi PZ=n(X=k)= Cknx0,5n si k < n.
X suit la loi binomiale B(n ; 0,5) ; PZ=n(X=k)= Cknx0,5k x0,5n-k.
4. Soit deux entiers k et n tous les deux inférieurs ou égaux à N.
a. Donner la valeur de P((Z=n) n (X=k)) si k > n.
k ne peut être supérieur à n : P((Z=n) n (X=k)) =0.
b. Montrer que si 0 < k < n < N alors : P((Z=n) n (X=k)) =Ckn CnN 5N-n / (2n x6N).
PZ=n(X=k)= Cknx0,5n .
P(Z = n) = CnN (1/6)n (5/6)N-n=CnN (1/6)N (5)N-n.
P((Z=n) n (X=k)) =PZ=n(X=k) x P(Z = n), les événements lancer du dé et lancer de la pièce étant indépendants.
5.a. Montrer que les événements (Z=0), (Z-1)...., (Z=n) forment un système complet d'évenements.
Soit Di l'événement " le dé tombe sur la face i" lors d'un lancer. Cette probabilité P(Ai) n'est pas nulle.
Il est impossible que le dé tombe sur deux faces différentes lors du même lancer. P(Ai n Aj) = 0.
Il y a toujours un événement de E qui est réalisé. P(E1 u E2 u E3 u E4 u E5 u E6) =1.
Les événements (Z=0), (Z-1)...., (Z=n) forment un système complet d'évenements.
b. Ecrire la formule des probabilités totales pour calculer P(X=0) en utilisant le système complet de la question précédente.
P(Z=0) = C0N(1/6)0x(5/6)N ; P(X=0)= 0 ;
P(Z=1) = C1N(1/6)1x(5/6)N-1 ; P(X=0)= P(Z=1) x1 /2 ;
P(Z=2) = C2N(1/6)2x(5/6)N-2 ; P(X=0)= P(Z=2) x(1 /2)2 ;
puis faire la somme.
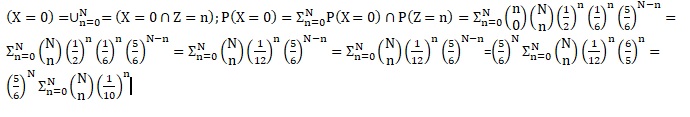
c. En déduire que :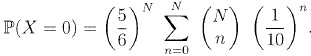
P(Z=1) = C1N(1/6)1x(5/6)N-1 =(5/6)N x C1N(1/6)1x(6 /5) ; P(Z=1) x1 /2 =(5/6)N x C1N 1 /10.
P(Z=2) = (5/6)N x C2N(1/6)2x(6/5)N-2 ; P(Z=2) x(1 /2)2 =(5/6)N x C2N (1 /10)2.
Puis faire la somme.
d. En déduire P(X=0) sous la forme (a / b) N où on donnera les valeurs de a et b.
Formule du binôme de Newton :
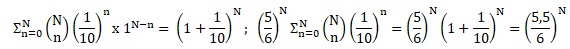
6. En déduire P(X=N).
7. Pour tout k appartenant à [1 ; N-1], expliciter p(X=k).
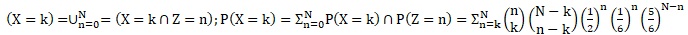
8. Justifier que X et Y ont la même loi.
Chaque
lancer de la pièce est une expérience de Bernoulli ; le succès
est d'obtenir pile ; sa probabilité est p = 1 /2 = constante.
X suit la loi binomiale B(Z ; 0,5).
L'échec est d'obtenir face ; Y suit la loi binomiale B(Z ; 0,5).
9. Donner l'espérance de X. On pourra utiliser la question 2.
Espérance E(X) = Z / 2.
Espérance E(Y) = Z / 2.
Espérance E(Z) = N / 6.
E(X+Y) =E(X) +E(Y) = E(Z) ; E(X)=N / 12.
|