Math�matiques, concours interne ing�nieur territorial 2021 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicit�s adapt�es � vos centres d’int�r�ts. .. .. . . .. .. ...... ... Plrobl�me 2. (3,5 points). Un pont d'une seule arche de longueur 16 m enjambe une route � double circulation. La partie sup�rieure du pont est � 5 m au dessus du niveau de la route. 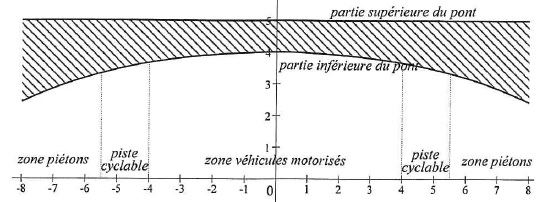La partie inf�rieure du pont est la courbe repr�sentative C d'une fonction f d�finie sur [-8 ; +8] par f(x) = a-(e0,2x+e-0,2x) /2 avec a r�el. C passe par le point de coordonn�es (0 ; 4).   1.a. Montrer que a = 5. f(0) = 4 = a-(e0+e0) / 2 = a-(1+1)/2 = a-1 ; a = 5. 1.b. Quelle est la propri�t� de la fonction f qui correspond � la sym�trie de la partie inf�rieure du pont par rapport � l'axe des ordonn�es ? f(x) = f(-x) ; cette fonction est paire ; sa courbe repr�sentative est sym�trique par rapport � l'axe des ordonn�es. 2.a Montrer que la d�riv�e  f '(x) = 0,1e-0,2x(1-e0,4x). f '(x) = -0,5 ( 0,2e0,2x-0,2e-0,2x) =0,1(e-0,2x-e0,2x) =0,1 (e-0,2x-e0,4x e-0,2x). f '(x) = 0,1e-0,2x(1-e0,4x). 2.b. Justifier que f est d�croissante sur [0 ; 8]. 0,1e-0,2x �tant strictement positif, le signe de f '(x) est celui de 1-e0,4x. 1-e0,4x=0 ; e0,4x = 1 = e0  ; 0,4x = 0 soit x = 0. 1-e0,4x < si x > 0.  f '(x) < 0 sur [0 ; 8] et f(x) est d�croissante sur cet intervalle. 3. Un camion de 2,5 m de largeur doit passer sous le pont au milieu de la file de droite de la zone  des v�hicules motoris�s. Quelle doit �tre la hauteur maximale de ce camion sachant que l'on doit laisser une lauteur de s�curit� minimale de 50 cm au dessus du camion. Les bords du camion passent aux abscisses x =0,75 et x = 3,25 m. Hauteur maximale du camion : h = f(3,25)-0,5. f(3,25) = 5-(e0,65+e-0,65) /2 =5-(1,9155 -0;522) / 2 = 5-0,697 ~4,30 m. h = 4,30-0,50 = 3,80 m. 4.a On veut peindre les deux facades de ce pont. Montrer que l'int�grale suivante est �gale � 5(e1,6-e-1,6). En d�duire que l'aire de la surface � peindre est environ 47,51 m2. 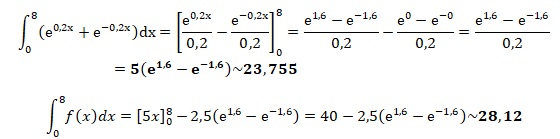Aire d'une face � peindre : 16 x5 -2 x28,12 =23,76 m2. Aire de deux faces : 47,52 m2. 4.b La peinture est vendue par bidon de 30 litres. Cette peinture a une propri�t� de recouvrement de 0,3 m2 par litre. Il faut deux couches de peinture. Combien de bidons au minimum sont n�cessaires ? Surface de peinture : 2 x47,52 =95 m2. Volume de peinture : 95 / 0,3 ~317 L soit 11 bidons. .... Probl�me 1. 3 points. Chacune des deux questions suivantes comporte trois propositions. Chacune de ces propositions est vraie ou fausse. Vous devez indiquer sur votre copie la lettre de la proposition avant de signaler si elle est vraie ou fausse.  Pour chaque question, il est possible que les trois propositions soient toutes vraies ou toutes fausses ; le nombre de r�ponses vraies ou fausses est variable selon les questions.  A chaque r�ponse correcte est attribu� 0,5 point. Question 1. � propos de la fonction f d�finie sur [0 ; +oo[ par f (x)=ln(2x+3)-x A : La fonction f est croissante, sur [0 ; +oo[. Faux. f '(x) = 2 /(2x+3)-1 = -(2x+1) / (2x+3) < 0 sur [0 ; +oo[ ; f(x) d�croissante. B : Le nombre d�riv� f '(1) vaut -0,6. Vrai. f '(1) = -3 / 5 = -0,6. C : Un arrondi au centi�me pr�s de l’int�grale suivante est 0,87. Faux. 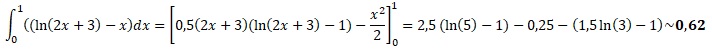Question 2. � propos de la suite d�finie par : u0=1 et un+1 = 0,8un+2  pour tout entier naturel n. D : Tous les termes de la suite (un ) sont positifs. Vrai. un+2 = 0,8un+1+2 ; un+2 -un+1= 0,8 un+1+2-0,8un-2 =0,8(un+1-un). Le signe de un+2 -un+1 est �gal au signe de un+1-un. D�monstration par r�currence : Initialisation : u1-u0 = 0,8 > 0, la propri�t� est vraie au rang z�ro. H�r�dit� : la propri�t� est vraie au rang n. un+1 -un >0. Or le signe de un+2 -un+1 est �gal au signe de un+1-un. un+2 -un+1 >0. Conclusion :La suite (un) est croissante et u0 = 1. E : u4 =3946 / 625. Vrai. u1 = 2,8  ; u2 = 4,24 ; u3 = 5,392 ; u4 = 6,3136 = 3946 / 625.   F : un tend vers plus l'infini si n tend vers plus l'infini. Faux. On pose vn = un-10. vn+1 = un+1-10=0,8 un +2-10 = 0,8(un-10) = 0,8 vn. (vn) suite g�om�trique de raison 0,8 et de premier terme -9. vn = -9 *0,8n ; un = vn +10 = -9 *0,8n +10. Quand n tend vers plus l'infini, 0,8 n tend vers z�ro et un tend vers 10. Probl�me 3. 3,5 points. Pour un triangle ABC quelconque dont les longueurs des c�t�s et les mesures des angles sont not�es : BC = a, AC = b, AB = c, a2 = b2 +c2 -2bc cos A. ( formule d'Al-Kashi). a / sin A = b / sin B = c / sin C ( loi des sinus). On consid�re un triangle ABC de mesures BC = 7, AC = 6, AB = 5. Question 1 (1 point) 1a. Montrer que cos(A) = 1 /5 et cos(B)= 19  / 35. (0,75 point) a2 = b2 +c2 -2bc cos A. cos A = (b2 +c2 -a2) / (2bc) =(62+52-72) / (2 x 5 x 6)=1 / 5. b2 = a2 +c2 -2ac cos B. cos B = (a2 +c2 -b2) / (2ac) =(72+52-62) / (2 x 5 x 7)=38 / 70 = 19 / 35. 1b. En d�duire sin(A ) et sin(B). (0,25 point). sin2 A = 1 -cos2 A = 1-1 / 25 =24 / 25. sin A = 24� / 5. sin2 B = 1 -cos2 B = 1-(19 / 35)2 =864 / 352. sin B = 864� / 35. 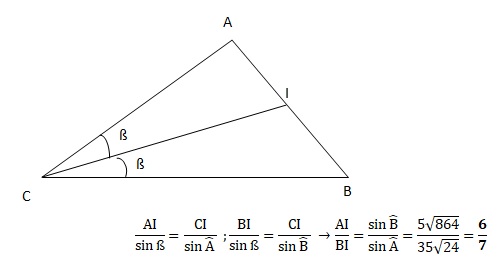La bissectrice de l’angle C coupe le c�t� [AB] au point I (les deux angles BCI et ACI sont �gaux). 2a. En utilisant deux fois la loi des sinus, une fois pour le triangle ACI et une fois pour le triangle BCI, montrer que AI / BI =6 / 7 . (0,75 point) 2b. Donner AI+BI. En d�duire AI et BI. (0,5 point) AI+BI = AB = 5. (AI+BI) / BI = (6+7) / 7 ; BI = 7 AB / 13 = 35 / 13. AI = 5-35 /13 = 30 / 13. 2c. Calculer CI. (0,25 point). CI 2= AC2 +AI2 - 2 AI x AC cos A=36+(30 / 13)2-2 x 6 x30 / 13 x 1 / 5 = 36+900 / 169- 72 / 13 =(6084  +900 -936) / 169 =6048 / 169. CI =6048� / 13. 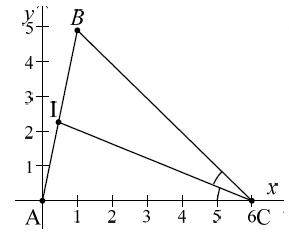Question 3 (1 point) Le triangle ABC est dispos� dans un rep�re orthonorm� du plan comme indiqu� sur la figure ci-dessous : Calculer les coordonn�es de B, les coordonn�es de I, l’aire du triangle ABC et la valeur du rapport aire de AIC / aire de BIC. AB2 = xB2 +yB2=25. BC2 = (6-xB)2 + yB2=49. 49-25 =(6-xB)2 -xB2 =24. 36-12 xB = 24 ; xB = 1 , yB = 24 �. AI2 =xI2 +yI2=(30 / 13)2. CI2 = (6-xI)2 + yI2=6048 / 169 (6-xI)2 -xI2 =(6048-900) / 169 =5148 / 169. -12xI+36=5148 / 169 ; 12xI =936 / 169 ; xI =78 / 169 = 6 / 13. yI2=900 / 169 -(78 / 169)2 =(900x169 -782) / 1692 =146 016 / 1692= 864 / 169 ;  yI = 864� / 13. Aire du triangle ABC : AC x yB / 2 = 6 x 24� / 2 = 3 x24�. Aire du triangle AIC : AC x yI / 2 = 6 x 864� / 26 = 3 x 864�/ 13 = 3 x 6 x24�/ 13 = 18 x 24�/ 13. Aire du triangle BIC :3 x24�- 18 x 24�/ 13 = 21 x 24�/ 13. Rapport aire de AIC / aire de BIC : 18 / 21 = 6 / 7.

menu