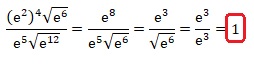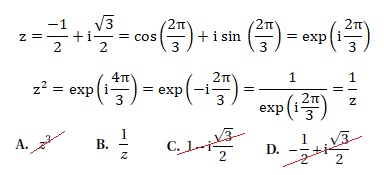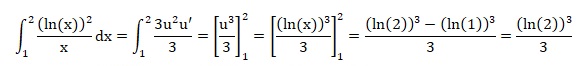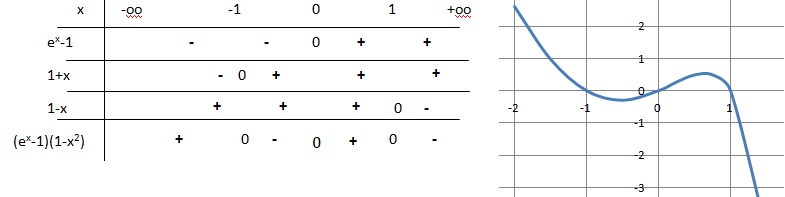Mathématiques,
concours ESA 2019. Ecole de santé des armées.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
..
..
.
..
.....
|
Exercice 1.
Pour chacune des questions, une seule des quatre affirmations A, B, C ou D est exacte.
On demande au candidat d’indiquer sans justification la réponse qui lui parait exacte en cochant la case sur la grille prévue à cet effet.
Toute réponse juste est comptée +1 point, toute réponse fausse est comptée −0,25 point. Une absence de réponse est comptée 0 point. Si le total est négatif, la note est ramenée à 0.
QCM1.
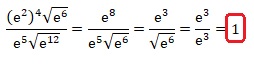
A. 0 : B. 1 vrai ; C. e ; D. e-2.
QCM2. L'équation | ln(x) | >0 a pour solution :
Si x appartient à ]0 ; 1[, | ln(x) | = -ln(x), strictement positif.
Si x appartient à ]1 ; +oo[, | ln(x) | =ln(x), strictement positif.
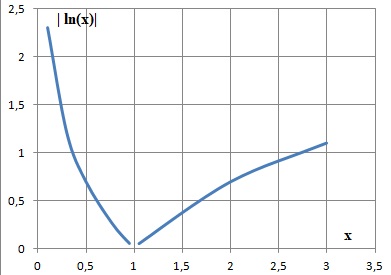
A. ]0 ; 1 [ u ]1 ; +oo[ vrai ; B. 1 ; +oo[ ; C. ]0 ; 1 [ ; D. ]1 ; +oo[.
QCM 3.
Dans une université de médecine où la moitié des étudiants travaille
sérieusement, 60% des élèves sont reçus au concours de fin d’année. De
plus, parmi ceux qui travaillent sérieusement, 90% réussissent le
concours.
Quelle est la probabilité qu’un étudiant réussisse le concours sachant qu’il n’a pas travaillé sérieusement ?
On défini les événements suivants :
T : travail sérieusement ; R : réussite au concours.
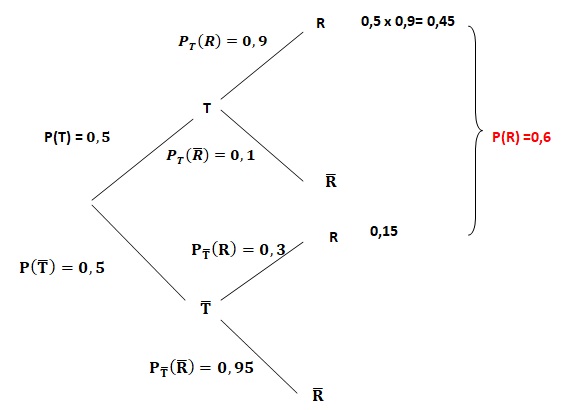
A. 0,3 vrai : B. 0,15 ; C. 0,01 ; D. 0,505.
QCM 4.Calculer z2 sachant que :
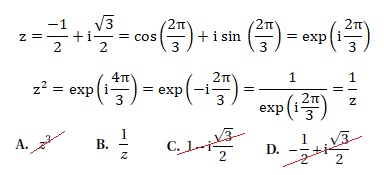
QCM 5. On pose u = ln(x) ; u' =1 /x.
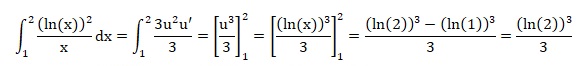
Réponse C.
QCM 6.
La durée d’efficacité d’un médicament, en heures, peut être modélisée par une variable aléatoire qui suit une loi exponentielle.
Quel est le paramètre l de cette loi sachant que P(X >20) = 0,3.
A. −ln(0,7) / 20 ; B. ln(0,3) / 20 ; C. -ln(0,3) / 20 vrai; D. 20 ln(0,3).
P(X > 20) = e-20l =0,3 ;
ln(0,3)=-20 l ; l = -ln(0,3) / 20.
|
| ..
... |
.
.
|
Exercice 2.
QCM 7.
L’ensemble des solutions de l’inéquation (ex −1) (1−x2) >0 est :
A. ]−∞; −1]∪[0 ; 1] vrai ; B. [−1 ; 0]∪[1 ; +∞[ ; C. [0; 1] ; D. ·[−1; 1].
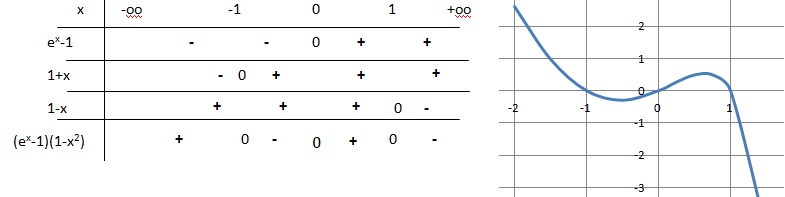
QCM 8.
La dérivée de la fonction f(x) = (e2x-1) / (e2x+1) définie sur R est :
On pose u = e2x-1 et v =e2x+1.
u' = 2e2x; v' = 2e2x;
(u'v-v'u) / v2 = [ 2e2x(e2x+1)-2e2x(e2x-1)] / (e2x+1)2.
f '(x)= [ 2e2x(e2x+1)-(e2x-1)] / (e2x+1)2.
f '(x) = 4e2x/ (e2x+1)2. Réponse D.
QCM 9.
La fonction f est définie sur R-{1} par f (x) = exp( x /(1−x)) . Laquelle de ces propositions est exacte ?
Quand x tend vers plus l'infini :
x / (1-x) = 1 / [1/x-1] tend vers -1.
f(x) tend vers e-1.
Quand x tend vers 1+ :
x / (1-x) tend vers -oo.
f(x) tend vers 0.
Quand x tend vers 1- :
x / (1-x) tend vers +oo.
f(x) tend vers +oo.
Réponse B.
QCM 10.
La suite (un) définie par un+1 = ln(1+un ) et u0 = 1 est :
A. croissante ; B. décroissante vrai ; C. convergente vers e ; D. divergente vers moins l'infini.
un+1 -un =ln(1+un ) -un.
Or ln(1+un ) < un ; donc un+1 <un.
n
|
0
|
1
|
2
|
3
|
4
|
un
|
1
|
ln(2) ~0,69
|
ln(1+ln(2)) ~0,526
|
ln(1+0,536)~0,423
|
ln(1+0,423) ~0,353
|
QCM 11.
On lance trois fois un dé équilibré, la probabilité d’obtenir exactement 2 fois le chiffre 6 est :
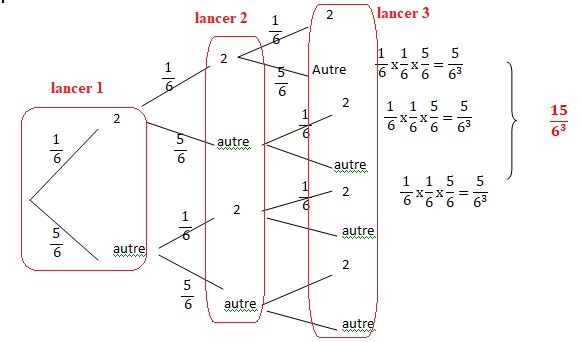
Réponse B.
QCM 12.
L’équation x2 ln(2) = x3 ln(3) a pour solution :
x = 0 est solution.
ln(2) = x ln(3) ; x = ln(2) / ln(3).
Réponse B.
|
..
..
|
. .
|
Exercice 3.
PARTIE A
Dans un pays une maladie virale est transmise d’un être humain à un autre par un insecte infecté.
Un test a été mis en place pour le dépistage de ce virus. On sait que :
• La probabilité qu’une personne atteinte par le virus ait un test positif est de 0,98.
• La probabilité qu’une personne non atteinte par le virus ait un test positif est de 0,01.
On procède à un test de dépistage systématique dans la population de ce
pays. Un individu est choisi au hasard dans cette population. On
appelle :
• M l’évènement : « l’individu est atteint par le virus » ;
• T l’évènement : « Le test de l’individu choisi est positif ».
On notera p la proportion de personnes atteintes par le virus dans la population.
1. Calculer p(T ).
2. Démontrer que la probabilité de M sachant T est donnée par la fonction f définie sur [0; 1] par f (p) =98p / (97p +1)
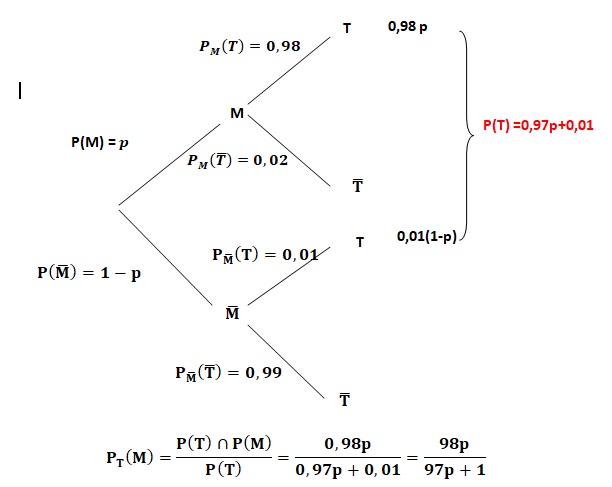
3. Étudier les variations de f .
On pose u = p ; v = 97p+1 ; u' = 1 ; v' = 97.
f '(x) =(u'v-v'u/) / v2 = [(97p+1)-97p] / (97p+1)2 = 1/ (97p+1)2 .
La dérivée est strictement positive ; la fonction f(p) est strictement croissante.
4. On
considère que le test est fiable lorsque la probabilité qu’une personne
ayant un test positif soit réellement atteinte par le virus est
supérieure ou égale à 0,95.
À partir de quelle proportion p,les malades dans la population le test est-il fiable?
Donner la valeur de p sous forme de fraction irréductible.
98p /(97p+1) >0,95.
98p > (97p+1) x0,95.
98p-97 x0,95p > 0,95.
(9800-95 x97)p > 95.
585 p > 95 ; p > 19 /117.
|
PARTIE B
Dans toute la partie B, un institut sanitaire estime que la probabilité qu’une personne soit atteinte par le virus est 0,15.
On choisit 100 individus au hasard dans cette population. Les tirages sont indépendants.
1. Soit X la variable aléatoire qui, aux 100 individus choisis, associe le nombre de personnes atteintes par le virus.
Déterminer la loi de probabilité X.
Loi binomiale.
Les tirages sont indépendants et deux issues sont possibles: être
atteinte par le virus p = 0,15 ; ne pas être atteint 1-p = 0,85.
2. Dans l’échantillon précédent, on dénombre 20 personnes atteintes par le virus.
Quelle conclusion peut-on tirer à propos de la valeur p = 0,15 au seuil de 95%?
Aide au calcul : 1,96×(0,15×0,85)½ ≈ 0,70 à 10−2 près.
On cherche un intervalle de fluctuation au seuil de 95 % :
1,96 (p(1-p) / n)½ = 1,96 (0,15 x0,85 / 100)½ ~0,70 / 10 = 0,07.
[0,15 -0,07 ; 0,15 +0,07] soit [0,08 ; 0,22].
La fréquence observée 20 / 100 = 0,20 appartient à cet intervalle. L'estimation p = 0,15 est correcte.
PARTIE C.
Dans cette partie, on suppose p inconnue.
On
choisit 100 individus au hasard dans la population. Les tirages sont
indépendants. On dénombre 20 personnes atteintes par le virus.
Donner un intervalle de confiance de p au seuil de 95%.
On cherche un intervalle de confiance au seuil de 95 % :
n > 30 ; n f = 20 > 5; n(1-f) = 80 >5.
Les conditions sont requises por définir un intervalle de confiance au seuil de 95 %.
1/100½ = 1 /10 = 0,10.
Fréquence observée : f = 20 / 100 = 0,20.
Intervalle de confiance : [0,20 -0,10 ; 0,20 +0,10) soit [0,10 ; 0,30 ].
PARTIE D.
Le
temps d’incubation en heures du virus peut être modélisé par une
variable aléatoire Y suivant une loi normale de moyenne 20 et
d’écart-type 5.
1. Que vaut P(15 < Y < 25) à 10−2 près ?
P(15 < Y) =0,158655 ; P(25 < Y) =0,841344 ;
P(15 < Y < 25)=0,841344 - 0,158655 ~0,68.
2. Que vaut P(Y > 15) à 10−2 près ?
P(Y > 15) = 1 -P(15 < Y) =1-0,158655 ~0,84.
3. Trouver a tel que P(Y < a) = 0,975 et interpréter le résultat obtenu.
La calculatrice conduit à : P(Y < 30) = 0,977.
P(Y < 29) =0,964.
On retient a = 30.
L'apparition des premiers symptômes apparaît dans un délai de 30 heures dans 97,5 % des cas.
|
|
|