Mathématiques, enseignement de spécialité, classe de première générale

Mathématiques, enseignement de spécialité, classe de première générale.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

.
.

...

.....

Exercice 1. QCM (5 points).
Une seule des 4 propositions est exacte.
• Question 1 :
Pour tout réel 𝑥, (e^x)³ est égal à : e^x * e³ ; e^x+3 ; e^3x vrai ; exp (x³).
(e^x)³ = e^x *e^x *e^x = e^3x.
• Question 2 :
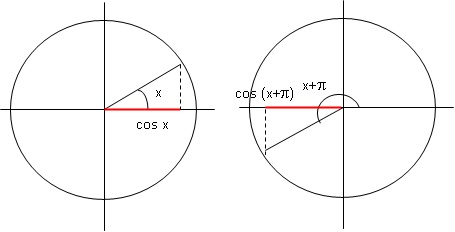
Pour tout réel x,cos(x+p) est égal à :
sin x ; - cos x vrai ; cos x ; -sin x.

• Question 3 :
On souhaite modéliser le niveau de la mer par une suite (u_n) de façon que u₀ représente le niveau de la mer, en mm, en 2003 et que u_n représente le niveau de la mer, en mm, n années après 2003.
Selon le site www.notre-planete.info/terre/climatologie_meteo, on constate une hausse assez rapide du niveau de la mer, qu’on estime à 3,3 mm par an depuis 2003.
Pour traduire ce constat, la suite (u_n) doit être :
a. une suite géométrique de raison 3,3.
b. une suite géométrique de raison 1,033.
c une suite arithmétique de raison 1,033.
d. une suite arithmétique de raison 3,3. Vrai.
Hausse de 3,3 mm par an : u_n = u₀ + 3,3 n.
• Question 4 :
Les figures ci-dessous représentent quatre polynômes du second degré dans un repère orthonormé et le signe de leur discriminant D. Parmi ces propositions, laquelle est juste ?

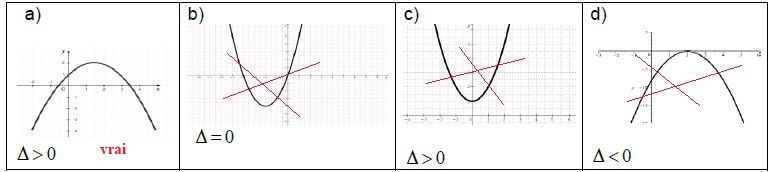
D = 0, la courbe est tangente à l'axe des abscisses.
D < 0, la courbe ne coupe pas l'axe des abscisses.
D > 0, la courbe coupe l'axe des abscisses en deux points distincts.
• Question 5 :
Le plan est rapporté à un repère orthonormé.
D est une droite dont une équation cartésienne est 2𝑥 − 𝑦 + 3 = 0.
Parmi ces propositions, laquelle est juste ?
a) La droite D passe par le point A de coordonnées (2 ; 1)
Si A appartient à la droite D : y_A =1 ; 2x_A+3 = 2*2+3 = 7; y_A diffère de 2x_A+3.
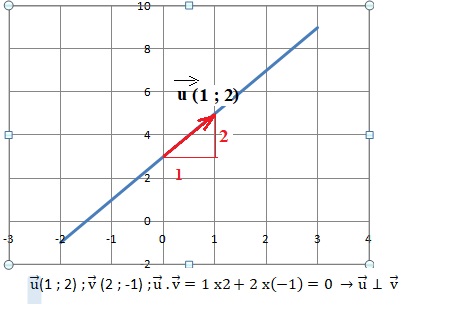
b) La droite D est dirigée par le vecteur de coordonnées (−1; 2)
Une droite d'équation réduite y = 2x+3 possède un vecteur directeur de coordonnée (1 ; 2).
c) Le vecteur de coordonnées (2; −1) est normal à la droite D. Vrai.

d) Le point d’intersection de la droite D avec l’axe des abscisses a comme coordonnées (0; 3).

.. ...

. .
Exercice 2. (5 points).
Une entreprise de menuiserie réalise des découpes dans des plaques rectangulaires de bois.
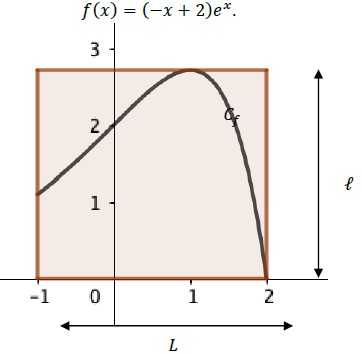
Dans un repère orthonormé d’unité 30 cm ci-dessous, on modélise la forme de la découpe dans la plaque rectangulaire par la courbe Cf représentative de la fonction f définie sur l’intervalle [−1;2] par f(x)=(−x+2)e^x.
Le bord supérieur de la plaque rectangulaire est tangent à la courbe Cf. On nomme L la longueur de la plaque rectangulaire et ℓ sa largeur.

1. On note f ' la fonction dérivée de f.
a. Montrer que pour tout réel x de l’intervalle [−1;2],f '(x) = (-x+1)e^x.
On pose u = -x+2 et v = e^x ; u' = -1 et v' = e^x.
u'v +v'u = -e^x +(-x+2)e^x =(-x+1)e^x.
b. En déduire le tableau de variations de la fonction 𝑓 sur [−1;2].
e^x est positif ; f '(x) = 0 pour x = 1.
Sur [-1 ; 1 [, f '(x) est positive et f(x) est strictement croissante.
Sur ]1 ; 2 ], f '(x) est négative et f(x) est strictement décroissante.

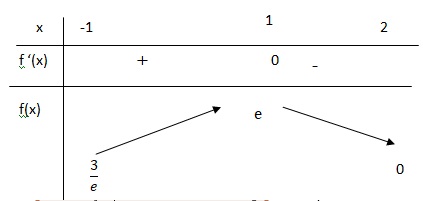
2. La longueur L de la plaque rectangulaire est de 90 cm. Trouver sa largeur ℓ exacte en cm.
La largeur correspond à f(1) = e soit en tenant compte des unités : l = 30 e cm.

. .

Exercice 3. (5 points)
Une compagnie d’assurance auto propose deux types de contrat :
– un contrat « Tous risques » dont le montant annuel est de 500 € ;
– un contrat « de base » dont le montant annuel est de 400 €.
En consultant le fichier clients de la compagnie, on recueille les données suivantes :
– 60% des clients possèdent un véhicule récent (moins de 5 ans). Les autres clients ont un véhicule ancien ;
– parmi les clients possédant un véhicule récent, 70% ont souscrit au contrat « Tous risques » ;
– parmi les clients possédant un véhicule ancien, 50% ont souscrit au contrat « Tous risques ».
On considère un client choisi au hasard.
D’une manière générale, la probabilité d’un événement 𝐴 est notée 𝑃(𝐴) et son événement contraire est noté 𝐴̅.
On note les événements suivants :
 𝑅 : « le client possède un véhicule récent » ;
 𝑇 : « le client a souscrit au contrat « Tous risques ».
On note 𝑋 la variable aléatoire qui donne le montant du contrat souscrit par un client.
1. Recopier et compléter l’arbre pondéré de probabilité traduisant les données de l’exercice.

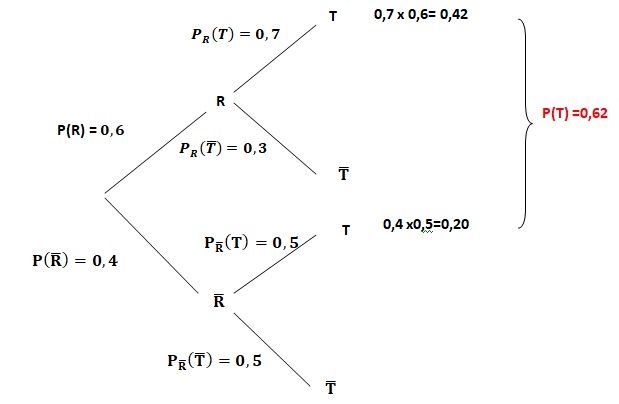
2. Calculer la probabilité qu’un client pris au hasard possède un véhicule récent et ait souscrit au contrat « Tous risques », c’est-à-dire calculer 𝑃(𝑅∩𝑇).
0,6 x0,7 = 0,42.
3. Montrer que 𝑃(𝑇)=0,62.
Formule des probabilités totales : 0,42 +0,20 = 0,62.
4. La variable aléatoire 𝑋 ne prend que deux valeurs 𝑎 et 𝑏. Déterminer ces deux valeurs, les probabilités 𝑃(𝑋=𝑎) et 𝑃(𝑋=𝑏), puis l’espérance de 𝑋.
a = 500 ; b = 400.
p(X=500) =P(T) = 0,62 ; p(X=400) =P(nonT) =1- 0,62= 0,38.
Espérance de X : 0,62 x500 +0,38 x400 = 462.

Exercice 4 (5 points).
En traversant une plaque de verre teintée, un rayon lumineux perd 20 % de son intensité lumineuse. L’intensité lumineuse est exprimée en candela (cd).
On utilise une lampe torche qui émet un rayon d’intensité lumineuse réglée à 400 cd.
On superpose n plaques de verres identiques (n étant un entier naturel) et on désire mesurer l’intensité lumineuse I_n du rayon à la sortie de la n-ième plaque.
On note I₀=400 l’intensité lumineuse du rayon émis par la lampe torche avant de traverser les plaques (intensité lumineuse initiale). Ainsi, cette situation est modélisée par la suite (I_n).
1. Montrer par un calcul que I₁=320.
I₁ = 0,8 I₀ = 0,8 x400 = 320.
2. a. Pour tout entier naturel n , exprimer I_n+1 en fonction de I_n.
I_n+1 = 0,80 I_n.
b. En déduire la nature de la suite (I_n). Préciser sa raison et son premier terme.
On passe d'un terme au suivant en le multipliant par 0,8. Il s'agit d'une suite géométrique de raison 0,80 et de premier terme I₀ = 400.
c. Pour tout entier naturel n, exprimer I_n en fonction de n.
I_n = 400 x 0,80ⁿ.
3. On souhaite déterminer le nombre minimal n de plaques à superposer afin que le rayon initial ait perdu au moins 70 % de son intensité lumineuse initiale après sa traversée des plaques.
a. Afin de déterminer le nombre de plaques à superposer, on considère la fonction Python suivante.
def nombrePlaques(J):
I=400
n=0
while I > J:
I = 0.8*I
n = n+1
return n
Préciser, en justifiant, le nombre J de sorte que l’appel nombrePlaques(j) renvoie le nombre de plaques à superposer.
I_n < 0,70 x400 ; I_n < 280. J = 280.
b. Le tableau suivant donne des valeurs de I_n. Combien de plaques doit-on superposer ?

n
0
1
2
3
4
5
6
7

I_n
400
320
256
204,8
163,84
131,07
104,85
83,886

400 x0,70 = 280 ; il faut superoser 2 plaques.
..

menu