Fonctions, tableaux de signe, mathématiques, classe de première.

Fonctions, tableaux de signe, mathématiques, classe de première.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

.
.

. ..

.....

1. Donner les tableaux de signes de :
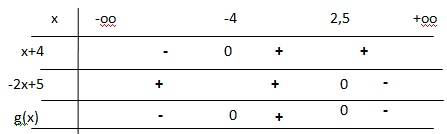
a). g(x) = (x+4)(-2x+5).
x+4 =0 , soit x = -4.
-2x+5 = 0 soit 2x = 5 et x = 2,5.

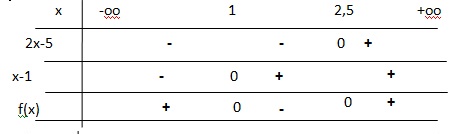
b). f(x) = (2x-5) -(2-x)(2x-5).
On factorise : f(x) = (2x-5) [1-(2-x)].
f(x) = (2x-5)(1-2+x).
f(x) = (2x-5)(x-1).
2x-5 = 0, soit 2x =5 et x = 2,5.
x-1 = 0 soit x = 1.

c). Réduire au même dénominateur puis établir le tableau de signes.

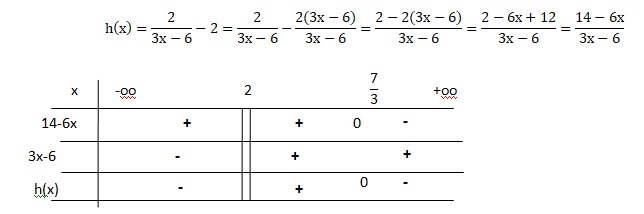
Exercice 2.
Soit la fonction g dont on donne la représentation graphique. Les réponses seront données avec la précision permise par le graphique.

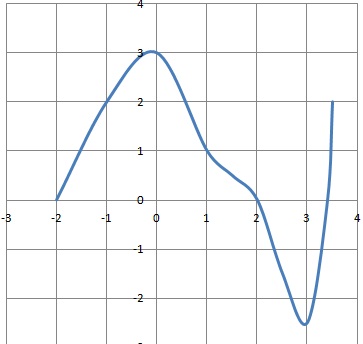
1. Quelles sont les images de -1 et de 0 ?
L'image de -1 est g(-1) = 2. L'image de 0 est g(0) = 3.
2. Quels sont les antécédents de -2,5 et 1 ?
L'antécédent de -2,5 est 3. Les antécédents de 1 sont : 1 ; environ -1,5 et environ 3,4.
3. Résoudre graphiquement f(x) = 2.
Solutions { -1 ; ~1,6 ; ~3,5 }.
4. Dresser le tableau de variations de g(x) sur l'intervalle [-2 : 3,5].

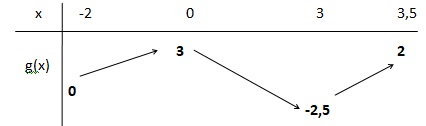
5. Soit f la fonction définie sur R par f(x) = -x+1.
a. Représenter la coube associée à la fonction f(x) sur le graphe précédent.

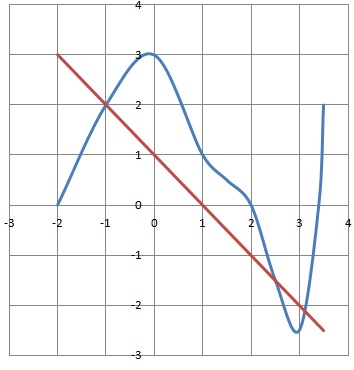
La droite passe par les points de coordonnées (0 ; 1) et (1 ; 0).
b. Quelles sont les solutions de l'équation g(x) = f(x) ?
Les courbes se coupent aux points d'abscisses : { -1 ; ~2,4 ; ~ 3,2 }.

.. ...

. .

Exercice 3.
Soit f la fonction définie sur R par g(x) = -x² +2x +2.
1. Quel est le nom de la courbe correspondante ?
Il s'agit d'une parabole.
2. La représenter et donner l'équation de son axe de symétrie.
a = -1 ; b = 2 ; -b / (2a) = -2 / (2(-1))= 1.

3. Donner le tableau de variation de g.

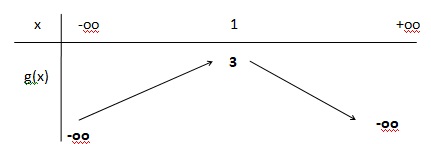
4. Calculer g(1) et g(3).
g(1) = -1² +2*1+2 = 3 ; g(3) = -3² +2*3+2 = -9+6+2= -1.
5. Soit M le point de la courbe d'abscisse 0 et P le point de la courbe d'abscisse 3.
Calculer le taux de variation de f entre M et P.
M(0 ; 3 ) ; P( 3 ; -1).
Taux de variation demandé : [g(x_P) -g(x_M)] / (x_P-x_M) =(-1-3) / (3-0) = -4 / 3.

Exercice 4.
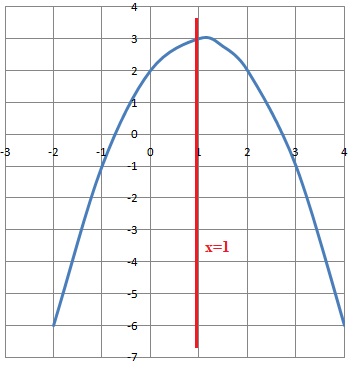
On considère la fonction f définie sur l'intervalle [-2 ; 4]. Sa courbe représentativeC est une parabole.

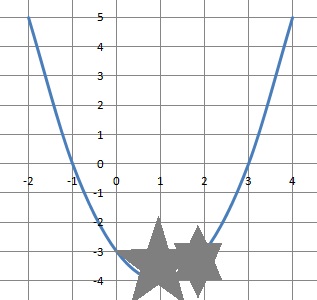
Une tache d'encre masque une partie de la courbe.
1. Lire sur le graphique l'image de -1 et de 3 par f.
f(-1) =0 ; f(3) =0.
2. Résoudre par lecture graphique sur l'intervalle [-2 ; 4], l'inéquation f(x) < 0.
x appartient à [-1 ; 3 ].
3. On admet que l'expression de la fonction f est de la forme f(x) = (x-x₁)(x-x₂) avec x₁ < x₂. Préciser les valeurs de x₁ et x₂.
f(x) = (x-x₁)(x-x₂) = 0 conduit à :
x-x₁ =0 soit x = x₁ = -1 et à x-x₂ =0 soit x = x₂ = 3.
Par suite f(x) = (x-(-1))(x-3)=(x+1)(x-3) = x² -3x+x-3 = x² -2x-3.
4. Retrouver les coordonnées du sommet de la parabole.
La courbe est symétrique par rapport à la droite d'équation x = 1.
Ou bien x = -b / (2a) = -(-2) / (2 *1) = 1.
f(1) = 1²-2*1-3 = -4.
5. Dresser le tableau de variations de f. On admet que f(-2) = f(4) = 5.

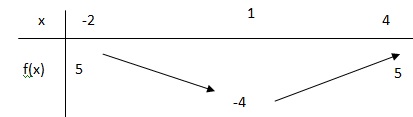
Exercice 5.
On considère la fonction f définie sur [-4 ; +4] par f(x) = x²-2x-3.
1. Calculer l'image de -1 par f.
f(-1) = (-1)²-2(-1)-3 =1+2-3=0.
2. Montrer que 3 est solution de f(x) = 0.
f(3) = 3² -2 *3 -3 = 9-6-3=0.
3. Donner une forme factorisée de f(x).
f(x) = (x-3)(x-(-1)) =(x-3)(x+1)..
4. Dresser le tableau de signes de f sur cet intervalle.

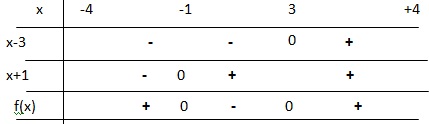
5. Déterminer quelle courbe représente la fonction f. Justifier.

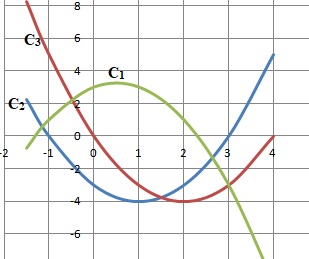
C₁ ne convient pas : elle est positive sur [-1 ; 2 ].
C₃ ne convient pas : elle est négative sur [0 ; 4 ].
C₂ convient : elle est négative sur [-1 ; 3 ].

Exercice 6.
Une entreprise commercialise des chocolats. La production hebdomadaire maximale est de 30 000 chocolats. On suppose que la totalité est vendue chaque semaine. les charges de production, en euros, pour x milliers de chocolats vendus sont modélisées par la fonction C définie sur [0 ; 30 ] par C(x) = 4x² +4x+520.
Prix de vente d'un chocolat : 0,128 €.
Pour la vente de x milliers de chocolats le chiffre d'affaires, en euros, est donné par la fonction R définie sur [0 ; 30 ) par R(x) = 128 x.
C_R et C_C désignent les courbes représentatives de R et C.

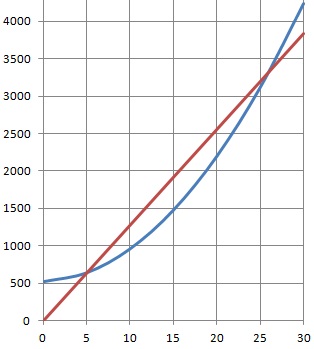
Le résultat réalisé pour x milliers de chocolats vendus est donné par la fonction B par B(x) = R(x) - C(x).
1. Montrer que B(x) = -4x² +124 x -520.
B(x) = 128 x -(4x² +4x+520) = -4x² +124 x -520.
2. Montrer que B(x) = -4(x-5)(x-26).
On développe : -4 ( x² -26x -5x +130)= -4 ( x² -31x +130)= -4x² +124 x -520.
3. En déduire le tableau de signe de B(x).

4. Déterminer les quantités de chocolat à produire pour obtenir un résultat positif.
x doit être compris entre 5000 et 26 000 chocolats , ]5000 ; 26 000 [.
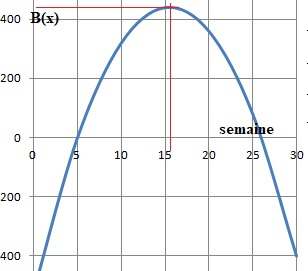
5. Quelle est la quantité de chocolat à produire pour maximiser le bénéfice habdomadaire ? Donner sa valeur.
B(x) = -4x² +124 x -520.
x = -b / (2a) = -124 / (2 *(-4))=124 / 8 =15,5.
B(15,5) = -4 *15,5²+124*15,5 -520= -961 +1922-520=441 €.

. .

Exercice 7.
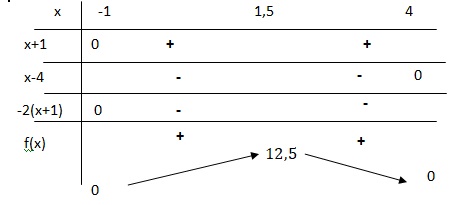
Soit f la fonction définie sur R par f(x) = -2x²+6x+8.
1. Montrer que f(x) = -2(x+1)(x-4).
On développe : -2 ( x²+x-4x-4) = -2(x²-3x-4) = -2x²+6x+8.
2. Résoudre l'équation f(x) = 0.
x+1=0 ; x = -1 ; x-4=0 ; x = 4.
3. Faire un schéma de l'allure de la courbe représentative de f.

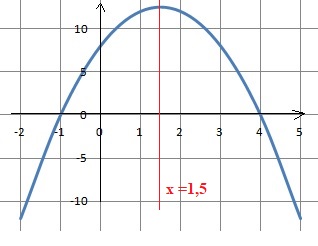
4. Expliquer pourquoi le maximum est atteint pour x = 1,5.
Le maximum est atteint pour x = -b / (2a) soit x = -6 / (2 *(-2)) = 6 / 4 = 1,5.
l'axe de symétrie de la courbe est la droite d'équation x = 1,5.
5. Dresser le tableau de variation de f sur l'intervalle [-1 ; 4].

.

menu